尽管求最短路的算法很多，但主要是对网络进行无条件求解。面对实际应用中复杂多样的具体要求，往往对最短路有附加的限制条件，这种情况下，再单纯地使用这些算法，就不能对有限制条件的最短路问题进行有效计算，因此有必要在经典算法的基础上，构造满足限制条件的最短路算法。

下面针对5种限制条件，在Dijkstra算法基础上，给出相应的算法思路。

1.最短路必须经过顶点vi

求解最短路时，先用Dijkstra算法求出起点到顶点vi的最短路，再用Dijkstra算法求出顶点vi到终点的最短路，然后将两个最短路合二为一即可。

2.最短路不能经过顶点vj

求解最短路时，将网络图G转换为不包含约束顶点vj的新网络图Gn，即将约束顶点vj以及关联的边从网络图G中去掉，然后用Dijkstra算法求出新网络图Gn中起点到终点的最短路即可。

3.最短路必须经过顶点vi但不能经过顶点vj

求解最短路时，将网络图G转换为不包含顶点vj的新网络图Gn，先用Dijkstra算法求出Gn中起点到顶点vi的最短路，再用Dijkstra算法求出Gn中顶点vi到终点的最短路，最后将两个最短路合二为一即可。

4.最短路如果经过顶点vi就不能经过顶点vj

针对要求，有两种可能：

（1）最短路如果没有经过顶点vi，那么经过或不经过顶点vj都没有关系；

（2）最短路径如果经过了约束顶点vi，就不能经过约束顶点vj。

求解最短路的思路是：

针对第（1）种可能，将网络图G转换为不包含顶点vi的新网络图Gn，然后用Dijkstra算法求出新网络图Gn中起点到终点的最短路。

针对第（2）种可能，将网络图G转换为不包含顶点vj的新网络图Gn，先用Dijkstra算法求出Gn中起点到顶点vi的最短路，再用Dijkstra算法求出Gn中顶点vi到终点的最短路，然后将两个最短路合二为一。

最后对第（1）种可能和第（2）种可能的最短路选择最短的一个即可。

5.最短路如果经过顶点vi就必须经过顶点vj

针对要求，有两种可能：

（1）最短路径如果没有经过约束顶点vi，那么经过或不经过顶点vj都没关系；

（2）最短路径如果经过了顶点vi，就必须经过顶点vj。

求解最短路的思路是：(www.daowen.com)

针对第（1）种可能，将网络图G转换为不包含顶点vi的新网络图Gn，然后用Dijkstra算法求出新网络图Gn中起点到终点的最短路。

针对第（2）种可能，用Dijkstra算法求出网络图G中起点到顶点vi的最短路，再用Dijkstra算法求出网络图G中顶点vi到顶点vj的最短路，再用Dijkstra算法求出顶点vj到终点的最短路，然后将三个最短路径合并。

最后对第（1）种可能和第（2）种可能的最短路选择最短的一个即可。

下面通过两个示例，介绍以上所述限制条件下的最短路求解问题。

例9.25　某公共交通区域网如图9.120所示，边的数据表示距离，现在需要在站点v1和站点v10之间开通一条关于距离最短的新公交线路，要求新公交线路如果经过站点v6就不能经过站点v9。

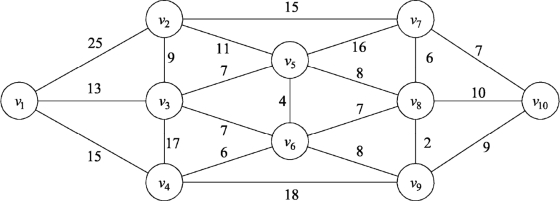
图9.120

解　用G表示图9.120的公共交通区域网，求解步骤如下：

（1）将网络图G转换为不包含约束顶点v6的新网络图Gn，然后用Dijkstra算法求出新网络图Gn中 v1 到 v10 的最短路（求解过程省略），可得最短路为v1v3v5v8v10，长度为38。

（2）再将网络图G转换为不包含约束顶点v9的新网络图Gn，先用Dijkstra算法求出Gn中v1到约束顶点v6的最短路（求解过程省略），可得最短路为v1v3v6，长度为20；再用Dijkstra算法求出Gn中约束顶点v6到v10的最短路（求解过程省略），可得最短路为v6v8v10，长度为17；将两个最短路合二为一，那么G中必须经过v6但不能经过v9的最短路径为v1v3v6v8v10，总长度为20+17=37。

（3）对两种可能的最短路取最短的一个，则在此问题的公共交通区域网中，如果经过站点v6就不能经过站点v9的新公交线路为v1→v3→v6→v8→v10，最短路的长度为37。

例9.26　某市一自来水规划管网如图9.121所示，边的数据表示距离，现在需要在顶点v1和v10之间铺设一条关于距离最短的新的自来水管路，要求新铺设的自来水管路如果经过顶点v6，就必须经过顶点v9。

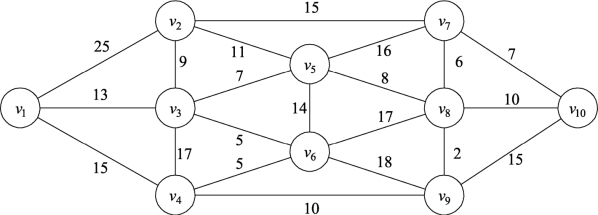
图9.121

解　用G表示图9.121的自来水规划管网，求解步骤如下：

（1）将网络图G转换为不包含约束顶点v6的新网络图Gn，然后用Dijkstra算法求出新网络图 Gn 中 v1到 v10的最短路（求解过程省略），可得最短路为v1v3v5v8v10，长度为38。

（2）用Dijkstra算法求出网络图G中v1到v6的最短路（求解过程省略），可得最短路为v1v3v6，长度为18；再用Dijkstra算法求出网络图G中v6到v9的最短路（求解过程省略），可得最短路为v6v4v9，长度为15；再用Dijkstra算法求出v9到v10的最短路（求解过程省略），可得最短路为v9v8v10，长度为12；将三个最短路合并，那么G中必须经过v6又必须经过v9的最短路径为v1v3v6v4v9v8v10，总长度为18+15+12=45。

（3）对两种可能的最短路取其短的一个，则在此问题的自来水规划管网中，如果经过顶点v6就必须经过顶点v9的新自来水管路为v1→v3→v5→v8→v10，最短路长度为38。

特别提示

通过上面两个示例，简单说明了解决有限制条件的最短路应用问题。针对最短路要求经过某个边或某个链路等问题，可以不必建立复杂的算法，只在以上算法思路的基础上，进行相应的扩展应用即可。