上节讨论了寻找网络中最小费用流的问题，但有时还要求在满足最小费用的同时，流量要求达到最大，这就是所谓的最小费用最大流问题。最小费用最大流可以说是最小费用流问题的特殊情况，即最小费用最大流的目标流的流值为网络的最大流。

最小费用最大流的算法与最小费用流算法基本相似，把最小费用流算法作适当的变动即得到最小费用最大流的算法。

1.最小费用最大流算法Ⅰ

此算法是基于最小费用流算法Ⅰ而产生的，主要思路如下：

首先利用最大流算法的思路，判断网络的流值是否达到最大，然后做如下处理：

（1）如果已经达到最大流，可利用最小费用流算法Ⅰ，对流量的分布状态进行调整，使总费用达到最小。

（2）如果没有达到最大流，先利用最大流算法，把网络的流量调整为最大流，然后再利用最小费用流算法Ⅰ，对流量的分布状态进行调整，使总费用达到最小。

例9.20　求图9.104的最小费用最大流，边旁数字分别表示容量、流量、费用。

解　在图9.104中，存在几条增流链，说明网络的流量还没有达到最大，利用最大流算法，求出最大流，最大流的流值为6，如图9.105所示。

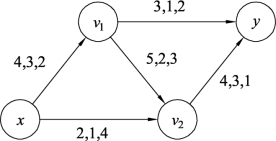
图9.104

构建图9.105的增流网络Gf，如图9.106所示。在图9.106中，经检查，存在负回路C=v1yv2v1，W(C)=2-1-3=-2<0，δ=min{1,4,2}=1，此负回路对应图9.105中的圈v1yv2v1为

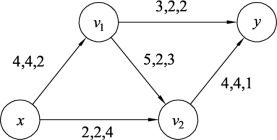
图9.105

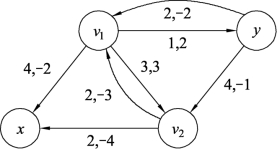
图9.106

增流圈。按照定理9.5，对图9.105中增流圈v1yv2v1的边(v1,y)加上δ=1，边(y,v2）、(v2,v1)减去δ=1，结果如图9.107所示。

对图9.107构建增流网络Gf，如图9.108所示。图9.108不存在负回路，说明图9.107已经是最大流值为6的最小费用最大流，总费用为W(f6)=4×2+2×4+1×3+3×2+3×1=28。

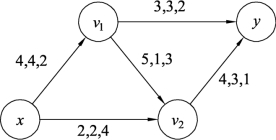
图9.107

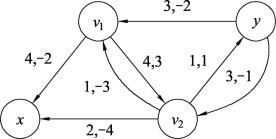
图9.108

2.最小费用最大流算法Ⅱ

此算法是基于最小费用流算法Ⅱ而产生的，唯一的差别是，把最小费用流算法Ⅱ中第三步的增加量δ 的计算公式改为δ=min{c′(e),e∈P*}即可，即不考虑目标流A的限制。

例9.21　求图9.109的最小费用最大流，边旁数字分别表示容量、流量、费用。

解　构建图9.109的增流网络Gf，如图9.110所示。

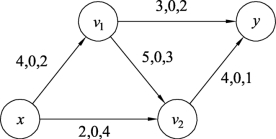
图9.109

对图9.110用标号法找出最短路P*=xv1y，W′(P*)=2+2=4，取流的增加量δ=min{c′(e),e∈P*}=min{4,3}=3。最短路径P*对应图9.109中的增流链为xv1y，对此增流链进行流量调整，结果如图9.111所示。继续对图9.111构建增流网络Gf，如图9.112所示。

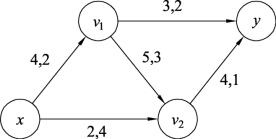
图9.110

在图9.112中，找出最短路P*=xv2y，W′(P*)=4+1=5，流的增加量δ=min{c′(e),e∈P*}=min{2,4}=2，最短路径P*对应图9.111中的增流链为xv2y，对此增流链进行流量调整，结果如图9.113所示。继续对图9.113构建增流网络Gf，如图9.114所示。

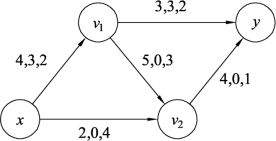
图9.111

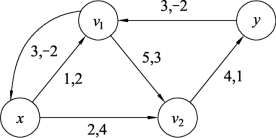
图9.112

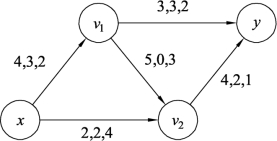
图9.113

图9.114中只有一条路径xv1v2y，取流的增加量δ=min{c′(e),e∈P*}=min{1,5,2}=1。最短路径P*对应图9.113中的增流链为xv1v2y，对此增流链进行流量调整，结果如图9.115所示。继续对图9.115构建增流网络Gf，如图9.116所示。

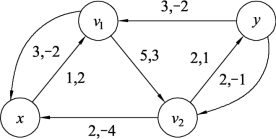(www.daowen.com)

图9.114

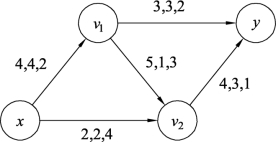
图9.115

在图9.116中，不存在从源x到汇y关于w′的路径P，说明图9.115已经达到最大流值为6的最小费用最大流，总费用W(fA)=4×2+2×4+1×3+3×2+3×1=28。

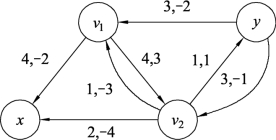
图9.116

特别提示

（1）最小费用最大流两个算法的特性差异和最小费用流两个算法的差异基本相同。

（2）通过上面两节的几个例题可以看出，追求的流量越大，付出的成本就越高。

3.最小费用最大流应用示例

例9.22　供销不平衡的运输问题。

有一个运输问题，有三个供应点x1、x2、x3，有三个需求点y1、y2、y3，供应量、需求量及单位运价如表9.11所示，在三个供应点x1、x2、x3处的储存费分别为2,3,1，请建立使运费和存储费之和最小的最大流网络模型。

表9.11　单位产品运价表

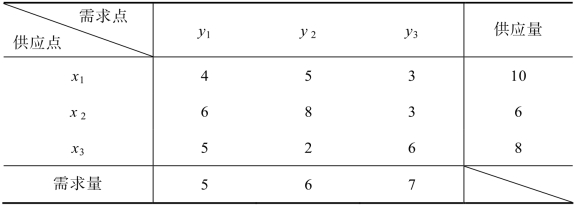
解　供应量之和为24，需求量之和为18，供应量剩余6，供需不平衡，即供大于求。由问题可知，剩余的物资需要支出储存费，问题的目标是运费和存储费之和最小，所以不但要考虑运输的最小费用最大流，还要考虑使存储费多的供应点尽可能剩余的物资少。

网络流是针对边讨论，这就需要把供应点存储费转化为边的问题。因此可假设剩余物资存储费相当于这些物资的运输费用，再虚设一个需求点y4，每个供应点均可以往y4运输，供应点到虚设需求点y4的边的费用分别是各个供应点的存储费；边的容量是剩余物资数量，其余边的容量为对应供应点需求量，费用分别是各个供应点运价。初始流量为0，这样就可以构建图9.117所示的网络图，边旁数字分别表示需求量、运输量、运输费用。

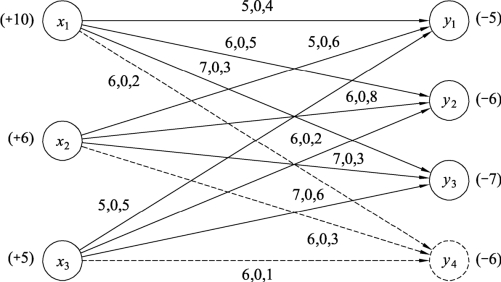
图9.117

图9.117是多源多汇的网络，按照规则转换为单源单汇的网络，然后再利用最小费用最大流算法求解即可。

例9.23　有转运点的运输问题。

在第5.3.3节中，给出了转运点的运输问题，此问题也可以用最小费用最大流求解。例题5.5的描述如下：某公司有三个产地A1、A2、A3，产量分别为7吨、4吨、9吨；有四个销售地B1、B2、B3、B4，销售量分别为3吨、6吨、5吨、6吨；同时还有一个转运地F。

运输过程有如下要求：

可知产地A1只能通过转运地F把物资转运出去；产地A2既可以直接把物资运送到销售地，也可以通过转运地F把物资运送到销售地；产地A3直接把物资运送到销售地而不通过转运地F；另外，转运地F只能把物资发送到销售地B2和B4。

运输过程中的单位产品运价如下：

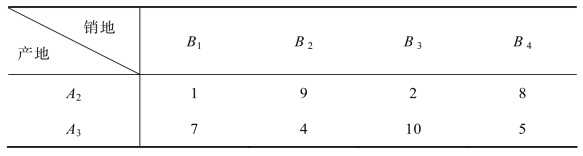
产地A1和转运地F之间的运价为3；产地A2和转运地F之间的运价为6；转运地F和销售地B2之间的运价为8；转运地F和销售地B4之间的运价为4；产地A2和A3到各个销售地的运价如表9.12所示：

表9.12　产地A2和A3到各个销售地的单位产品运价表

该公司应该如何调运才能使产品的总运费最少？

解　针对产地和销地是否有供求关系来构建运输网络的边，边的容量确定如图 9.118 所示，边的流量设为零流，边的费用为给出的运价，同时化为单源单汇。然后利用最小费用最大流算法求解即可。

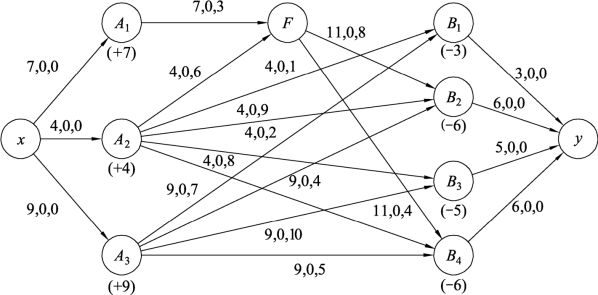
图9.118

例9.24　产品多样性的运输问题。

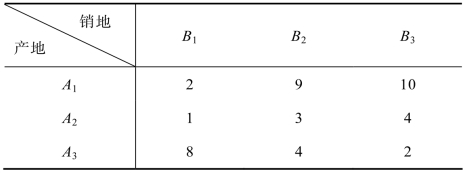
在第5.3.4节的例题5.7中，给出了产品多样性的运输问题，此问题也可以用最小费用最大流求解。例题5.7的描述如下：某集团公司有A1、A2、A3三个加工厂，A1生产Ⅰ和Ⅱ两种产品，产量分别为6吨和5吨；A2生产Ⅰ产品，产量为8吨；A3生产Ⅱ和Ⅲ两种产品，产量分别为4吨和12吨。有B1、B2、B3三个销售地，B1需要Ⅰ和Ⅱ两种产品，销量分别为6吨和5吨；B2只需要Ⅱ产品，销量为4吨；B3需要Ⅰ和Ⅲ两种产品，销量分别为8吨和12吨。从各工厂到销售地的单位产品的运价如表9.13所示，该公司应该如何调运才能使产品的总运费最少。

表9.13　单位产品运价表

解　产地总产品数量为35吨，销售地需求产品总量也为35吨，在产品总量上供销平衡。同时产品Ⅰ、Ⅱ和Ⅲ的产量和销量也分别相等，即每个单一产品也是供销平衡的。在思路上要把产品种类有多种的产地和销地拆分，针对A1生产Ⅰ和Ⅱ两种产品，用A1表示生产Ⅰ产品，用表示生产Ⅱ产品；针对A3生产Ⅱ和Ⅲ两种产品，用A3表示生产Ⅱ产品，用表示生产Ⅲ产品。同理，用B1表示需要Ⅰ产品，用表示需要Ⅱ产品；用B3表示需要Ⅰ产品，用表示需要Ⅲ产品。针对产地和销地是否有供求关系来构建运输网络的边，边的容量确定如图9.119所示，边的流量设为零流，边的费用为给出的运价，同时化为单源单汇。然后利用最小费用最大流算法求解即可。

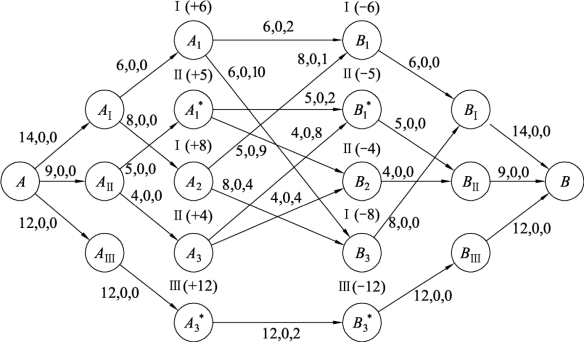
图9.119