在第9.3节中，把图的边赋予实数的权，学习了网络的极值问题；在第9.4.2节中把图的边赋给容量和流量，学习了网络的最大流问题。而在实际问题中，不但需要考虑网络流量的分配问题，还要考虑费用或代价尽可能低，这就提出了网络最小费用流问题。最小费用流问题同样是图论的核心问题之一。

下面给出的引例就说明了实际问题中的网络最小费用流问题。

例9.15　有一批货物需要从发送地v1运送到接收地v6，发送地v1有物资8吨，接收地v6需要6吨。运输网络如图9.75所示，其中v2、v3、v4、v5为转运点，边旁数字分别表示线路的输送能力及在该线路上输送单位货物所需的成本，即所谓运输网络的容量和权。那么如何

图9.75

派送才能使一定数量的货物以尽可能低的费用从发送地v1派送到接收地v6。

类似这样的问题，就是所谓的最小费用流问题，即在实际问题中，除了考虑网络的流量分配之外，还要考虑和输送成本有关的因素，如运输费用（与距离有关）等，这样在建立运输网络时，除了每条边赋予容量和流量外，同时也对应另外一个参数权。也就是说，在对运输网络分配流量时，除了考虑流量符合容量约束条件和流量守恒条件以外，还要考虑流程的大小。这些问题可以通过线性规划模型求解，但考虑到网络模型结构的直观性、形象性以及求解的整数性，建立最小费用流算法时就有其特定的优点。最小费用流算法是对运输网络分配一定的流值并使网络流费用最低的一种方法。

1.相关概念

在运输网络中，除了把边赋予表示成本、时间、距离等实数权以外，还要把边赋予容量和流量，由此可以给出运输网络另外一个定义：有运输网络G=(V,E,C,F,W,X,Y)，其中W表示费用，或仍称为权，可指距离、时间、成本等。在网络中用wij表示一个单位流量从顶点vi沿着边(vi,vj)到顶点vj时所需的费用。

如果设fA为运输网络G流值为A的一个网络流，即Valf=A，则W(fA)表示在运输网络G内按照fA的网络流从源到汇运送A个单位流量时所需的总费用，称W(fA)为网络流fA的费用，其表达式为

一般地，在运输网络G中，流值为A的网络流可能不止一个。若fA*为流值为A的所有网络流中费用最小的一个流，即W(fA*)=min{W(f) | f为G网络流，Valf=A}，则fA*称为运输网络G中流值为A的最小费用流。也就是说，最小费用流是按照网络流fA*从源到汇运送A个流量所花费的最小总费用。另外，当A为运输网络G的最大流的流值时，fA*称为运输网络G的最小费用最大流。

在最大流算法中，不考虑费用，通过寻找任意的增流链来增加网络的流量，而在最小费用流中，也是寻找增流链，但不能寻找任意的增流链，而是寻找关于费用最低的增流链来增加网络的流量。现在的问题就是，在运输网络中如何寻找关于费用最低的增流链。为了解决这个问题，下面给出构建增流网络的方法及相关知识。

2.伴随网络流f的增流网络

设f为运输网络G=(V,E,C,F,W,X,Y)的一个网络流，按照如下规则构建另外一个新的网络图Gf=(V,E,C′,W′,X,Y)，该网络图称为伴随f的增流网络。

第一步：Gf中的顶点仍然以G的顶点为顶点，即V(Gf)=V(G)。

第二步：Gf中的边按照如下规则构建：

（1）若G中边(u,v)的流量f(u,v)=0，即为零边时，则针对Gf构建一条同向边e=(u,v)，其中c′(u,v)=c(u,v)-f(u,v)=c(u,v)-0=c(u,v)，w′(u,v)=w(u,v)，如图9.76所示：

图9.76

这样构建新边的原因是，G的边(u,v)是零边，所以在增流链中只能成为流量增加的前向边，流量增加的最大量值是c(u,v)-f(u,v)，即c(u,v)，而费用也会随着增加，则有w′(u,v)=w(u,v)，如图9.77：

图9.77

（2）若G中边(u,v)的流量f(u,v)=c(u,v)，即为饱和边时，则针对Gf构建一条反向边e=(v,u)，其中c′(v,u)=f(u,v)，w′(v,u)=-w(u,v)，如图9.78所示：

图9.78

这样构建新边的原因是，G的边(u,v)是饱和边，所以在增流链中只能成为流量减少的后向边，流量减少的最大量值是f(u,v)，而费用也随着减小，则有w′(v,u)=-w(u,v)，如图9.79所示：

图9.79

（3）若 G 中边(u,v)的流量f (u,v)<c(u,v)，即为不饱和边时，则针对 Gf分别构建一条同向边e1=(u,v)和一条反向边e2=(v,u)。其中针对边 e1 有 c′(u,v)=c(u,v)-f(u,v)，w′(u,v)=w(u,v)；针对边e2有c′(v,u)=f(u,v)，w′(v,u)=-w(u,v)，如图9.80所示：

图9.80

这样构建新边的原因是，G的边(u,v)是不饱和边，所以在增流链中既能做流量增加的前向边，也能做流量减少的后向边。在成为前向边时，流量增加的最大量值是c(u,v)-f(u,v)，费用也随着增加，即有w′(u,v)=w(u,v)；在成为后向边时，流量减少的最大量值是f(u,v)，费用也随着减小，即w′(v,u)=-w(u,v)，如图9.81所示：

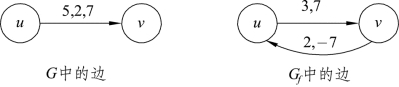
图9.81

按照上述规则，就可以基于运输网络G构建出它的增流网络Gf。在增流网络Gf中，如果P为一条基于w′的从源x到汇y的路径，则路径P在Gf中关于w′的长度为

根据构建增流网络的规则可以看出，在Gf中每一条关于w′的路径P都对应运输网络G中的一条增流链。若在Gf所有路径P中，选择最短的路径P*，即W(P*)=min{W(P)}，则路径P*对应运输网络G中的增流链就是关于费用最低的增流链；如果在该增流链上增加流量，就是在满足费用最低的要求下增加网络的流量，这也正是最小费用流算法的核心思路。

下面给出负回路和增流圈的概念：

在增流网络Gf中，如果存在基于w′的回路C，把满足以下条件的回路称为负回路：即负回路C中所有边的权之和小于0。

负回路对应运输网络G中一个圈，在这个圈中，如果方向与负回路方向一致的所有边都为不饱和边，同时，方向与负回路方向相反的所有边都为正边，那么这个圈称为增流圈。

特别提示

在增流网络Gf中，c′可以看作边的流量变化的最大量值，w′前面的符号可以表示该边是作为增流链的前向边还是后向边。

例9.16　图9.82给出了网络流f流值为4的网络图，边旁数字分别表示容量、流量、费用，试构建伴随f的增流网络。

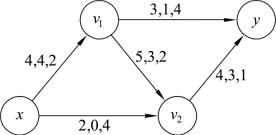
图9.82

解　边(x,v1)是饱和边，构建一条反向边；边(x,v2)是零边，构建一条同向边；其余边为非零的不饱和边，分别构建一条同向边和一条反向边。增流网络Gf如图9.83所示。

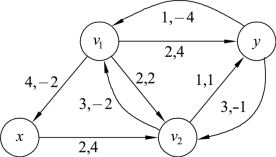
图9.83

在图9.83的增流网络中，从源x到汇y的路径有P1=xv2y和P2=xv2v1y，其中路长分别为

W(P1)=w′(x,v2)+w′(v2,y)=4+1=5

W(P2)=w′(x,v2)+w′(v2,v1)+w′(v1,y)=4-2+4=6

路径P1、P2分别对应图9.82中的增流链xv2y和xv21vy。又知最短路径是P1，那么费用最低的增流链即是x2vy。

另外，在图9.83的增流网络中，存在负回路。例如，逆时针走向的负回路C＝v1v2yv1，

其中W(C)=w′(v1,v2)+w′(v2,y)+w′(y,v1)=2+1-4=-1<0，此负回路对应于图9.82中的圈v1v2yv1。在这个圈中，边(v1,v2)和边(v2,y)的方向与负回路方向一致，并且均为不饱和边，同时，边（v1,y）方向与负回路方向相反，并且为正边，所以此圈也为增流圈。

3.相关定理

定理9.4　网络流fA为运输网络G中流值为A的最小费用流的充要条件是，在增流网络Gf中无负回路，即Gf中的任意一个回路C都有

定理9.5　设运输网络G中流值为A的网络流为fA，若增流网络Gf中存在负回路，对G分配流值为A的最小费用流的方法是：

（1）取δ=min{c′(e),e为Gf中负回路的边}。

（2）判断负回路对应G中的圈是否为增流圈；如果是增流圈，需对增流圈的流量进行调整，即把方向与负回路方向一致的所有不饱和边的流量加上δ，把方向与负回路方向相反的所有正边的流量减去δ。

定理9.5说明，可以在保持运输网络G的流值A不变的前提下，对运输网络G的网络流f的分布状态进行调整，从而得到流值A的最小费用流。

定理9.6　设运输网络G中流值为A的网络流为fA，若路径P为增流网络Gf中从源x到汇y的最短路径，令δ=min{c′(e),e为路径P中的边}，可知路径P对应G中的增流链Q的调整量l(Q)=δ，则fA的修改流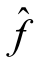为

则为G中流值等于A+δ的最小费用流。

定理9.6说明，在运输网络G中已经有初始最小费用流fA的基础上，进一步寻求流值大于原流值A的最小费用流的方法。

定理9.7　网络流f为运输网络G的最大流的充要条件是，伴随f的增流网络Gf中不含有从源x到汇y的路径。

从以上几个定理可知，构造增流网络的目的就是判断网络的流是否为最小费用流，或者网络的流值是否在满足费用最低的条件下达到所要求的目标流，这就为判断最小费用流提供了依据。

基于给出的相关概念、伴随网络流f的增流网络以及相关的定理等，可以给出最小费用流的算法。

4.最小费用流算法

常用的最小费用流算法有网络单纯形算法（Graph Simplex Algorithm）、连续最短路算法（Successive Shortest Path Algorithm）、松弛算法（Relaxation Algorithm）、消圈算法(Cycle-canceling Algorithm)、原始-对偶算法（Primal-dual Algorithm）、瑕疵算法(Out-of-Kilter Algorithm)等等，下面主要介绍Ford-Fulkerson的最小费用流算法。

（1）最小费用流算法Ⅰ。

此算法主要适用于：

① 初始流的流值已经达到给定的目标值，判定网络流f的分布是否满足总费用最小，若不满足，就调整流量的分布状态，从而使总的费用达到最低。

② 目标流的流值A给定，在初始流（或者是零流）的基础上，先把流量调整到流值A，然后再调整流量的分布状态，从而使总的费用最低。

算法的具体步骤如下：

第一步：如果运输网络G的流值没有达到A，先用最大流算法把流值调到A；如果运输网络G的流值达到A，则不对网络流进行调整。

第二步：针对流值为A的运输网络G，构建伴随网络流f的增流网络Gf 。

第三步：针对增流网络Gf，查看是否存在基于w′的负回路；如果不存在负回路，说明当前的网络流已经是最小费用流，算法终止，否则转到下一步。

第四步：针对存在的负回路C，令δ=min{c′(e),e为Gf中负回路的边}。

第五步：针对负回路C对应运输网络G中的圈，判断该圈是否为增流圈；如果不是增流圈，转到第三步继续寻找负回路，否则转到下一步。

第六步：针对运输网络G中的增流圈，按照定理9.5，把增流圈中方向与负回路方向一致的所有不饱和边的流量加上δ；把增流圈中方向与负回路方向相反的所有正边的流量减去δ。

第七步：继续寻找负回路，如果有负回路，继续调整，否则返回第二步。

下面通过例题来具体了解最小费用流算法Ⅰ的求解过程。(www.daowen.com)

例9.17　图 9.84 是网络流f的流值为5的（或者说已经把流值调整到5）网络图，边旁数字分别表示容量、流量、费用。判断是否为流值为5的最小费用流，如果不是，将当前的费用流调整成为最小费用流。

解　构建图9.84的增流网络Gf，如图9.85所示。

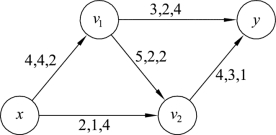
图9.84

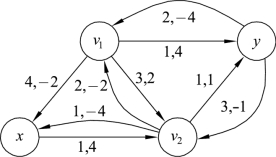
图9.85

图9.85中，有负回路C=v1v2yv1，W(C)=2+1-4=-1<0，取δ=min{c′(e)}=min{3,1,2}=1。

图9.85中的负回路v1v2yv1对应图9.84中圈v1v2yv1，可以看出，该圈为增流圈。按照定理9.5，对图9.84中增流圈v1v2yv1的边(v1,v2)、(v2,y)加上δ=1，边(y,v1)减去δ=1，结果如图9.86所示。再对图9.86构建增流网络Gf，如图9.87所示。

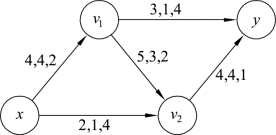
在图9.87中已经不存在负回路，说明图9.86已经是流值为5的最小费用流。在图9.84最初的网络流中，总费用W(f5)=4×2+1×4+2×2+2×4+3×1=27，而在图9.86中，总费用W(f5)=4×2+1×4+3×2+1×4+4×1=26，费用降低了1。

图9.87

另外，如果此问题需要求解将流值调整到6的最小费用流，也可用此算法求解，即利用最大流算法，先将图9.84的流值调整到6，然后再利用该算法调整流的分布状态。

特别提示

该算法的最大问题是，在增流网络中寻找负回路相对困难，尤其是对于节点或边较多的运输网络，寻找负回路的困难会更大。

（2）最小费用流算法Ⅱ。

此算法主要适用于：目标流的流值A给定，在初始流（或者是零流）的基础上，同时在满足费用最低的前提下，把流量逐步调整到流值A。

算法的具体步骤如下：

第一步：初始时运输网络G已给定网络流f，或者是零流。

第二步：构建伴随网络流f的增流网络Gf 。

第三步：在增流网络Gf中，判断是否存在关于w′的从源x到汇y的路径P，若不存在路径P，说明无法调整最小费用流，算法停止；否则利用标号法找出从源x到汇y关于w′的代数和最小的路径P*，令流的增加量δ=min{c′(e),e∈P*；A-Valf}。

第四步：最短路径P*对应运输网络G中的链即为一条由源x到汇y的增流链，和求最大流算法一致，对增流链中所有前向边的流量加上δ，所有后向边的流量减去δ，其他边的流量不变。

第五步：可知新的网络流为。若，说明当前的网络流已经是流值为A的最小费用流，算法终止；否则将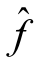视为网络流f，转到第二步。下面通过例题来具体了解最小费用流算法Ⅱ的求解过程。

例9.18　图9.88是网络流f的流值为4的网络图，边旁数字分别表示容量、流量、费用，试求将流值调整到6的最小费用流。

解　下面利用最小费用流算法Ⅱ对此问题求解。

构建图9.88的增流网络Gf，如图9.89所示。在图9.89中，有从源x到汇y关于w′的路径P，利用标号法可找出最短路径为xv2y和xv12vy。任意选择一个作为P*，这里选择P*=xv1v2y，流的增加量δ=min{1,3,1；6-4}=1。最短路径P*对应图9.88中的增流链为xv1v2y，对此增流链进行流量调整，结果如图9.90所示。图9.90的流值为5，还没有达到问题所要求的流值6，继续对图9.90构建增流网络Gf，如图9.91所示。

图9.88

图9.89

图9.90

在图9.91中，从源x到汇y只有一条路径xv2v1y，流的增加量δ=min{2,3,2；6-5}=1，对应图9.90中的增流链为xv2v1y，对增流链进行流量调整，结果如图9.92所示。

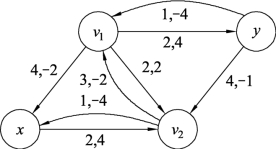
图9.91

针对图9.92，尽管流量还可以增加，但流值已经达到了要求的目标流6，说明已经得到将流值调整到6的最小费用流，总的最小费用为W(f6)=4×2+2×4+2×2+2×4+4×1=32。

下面对例9.18再用最小费用流算法Ⅰ求解一下，看看会有什么结果。

先利用最大流算法的思路，将图9.88的流值调整到6，如图9.93所示。然后利用最小费用流算法Ⅰ调整最小费用流的分布状态（过程省略），最终结果如图9.94所示。

图9.93

在图9.94中，流值为6的最小费用为W(f6)=3×2+3×4+1×2+2×4+4×1=32，而图9.92中流值为6的最小费用也为32，但仔细观察图9.92和图9.94，可以看出，两个网络图中流的分布状态不一样。

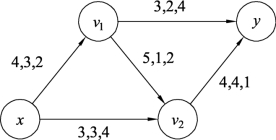
图9.94

图9.92

这也说明，在同样的最小费用流下，有可能出现流的分布状态是不同的。出现此类现象的原因是，在增流网络中，会同时出现两个以上权值一样的负回路（算法一）或两个以上的最短路径（算法二）。如在例9.18求解时，就同时出现过xv2y和xv1v2y两个最短路径，选择不一样的最短路径调整流量，也就出现了不同的流的分布状态。

为了更好地说明最小费用流算法Ⅰ和算法Ⅱ的差别，下面给出一个例题。

例9.19　图9.95是网络流f的流值为4的网络图，边旁数字分别表示容量、流量、费用。① 用最小费用流算法Ⅰ求流值为7的最小费用流。② 用最小费用流算法Ⅱ求将流值调整到7的最小费用流。

解　① 用最小费用流算法Ⅰ求流值为7的最小费用流。

首先将图9.95的流值调整到7，结果如图9.96所示。

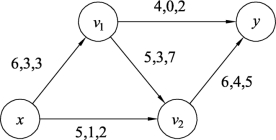
图9.95

构造图9.96的增流网络，如图9.97所示。在图9.97中有负回路xv2v1x和v1yv2v1，这里取W(C)最小的负回路v1yv2v1，其中W(C)=2-5-7=-10，δ=min{c′(e)}=min{3,6,5}=3，此负回路对应图9.96中的圈v1yv2v1为增流圈。按照定理9.5，对图9.96中增流圈v1yv2v1的流量进行调整，结果如图9.98所示。

图9.96

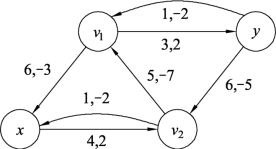
图9.97

继续对图9.98构造增流网络，如图9.99所示。

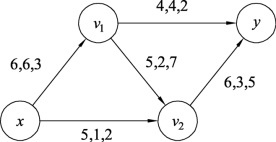
图9.98

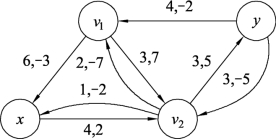
在图9.99中有负回路xv2v1x，其中W(C)=2-7-3＝-8，δ=min{c′(e)}=min{4,2,6}=2，此负回路对应图9.98中的圈xv2v1x为增流圈。按照定理9.5，对图9.98中增流圈xv2v1x的流量进行调整，结果如图9.100所示。继续对图9.100构造增流网络，如图9.101所示。

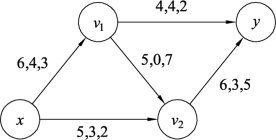
图9.100

在图9.101中已经不存在负回路，说明图9.100已经是流值为7的最小费用流，总费用W(f7)=4×3+3×2+0×7+4×2+3×5=41。

图9.101

② 用最小费用流算法Ⅱ求将流值调整到7的最小费用流。

首先构造图9.95的增流网络，如图9.102所示。

图9.102

在图9.102中，存在从源x到汇y关于w′的最短路径xv2v1y，其中流的增加量δ=min{4,3,4；7-4}=3。最短路径对应图9.95中的增流链为xv2v1y，对此增流链进行流量调整，结果如图9.103所示。

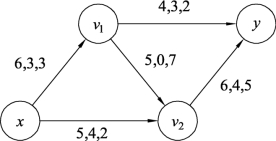
图9.103

图9.103中的流值已经达到了要求的目标流7，说明已经得到将流值调整到7的最小费用流，总的最小费用为W(f7)=3×3+4×2+0×7+3×2+4×5=43。

对上例两种算法的求解结果进行比较可以看出，在图9.100中，流值为7的最小费用为41；而图9.103中，流值为7的最小费用为43。这说明最小费用流算法Ⅱ求出的并不是流值为7的最小费用流。

造成这种结果的原因是，最小费用流算法Ⅰ就是使整个网络流的费用达到最低，而最小费用流算法Ⅱ是在初始流4的基础上，在满足费用最低的要求下，将流量由4调整到7，而图9.95中流值4本身就不是最小费用流。

这种现象也说明，最小费用流算法Ⅱ求出的不一定是流值为A的最小费用流，而是基于给定的初始流，在满足费用最低的要求下，将初始流调整到目标流，即最小费用流算法Ⅱ对给出的初始流是不是最小费用流不做考虑。

另外，如果想利用最小费用流算法Ⅱ求出流值为A的最小费用流，处理的思路就是先将给出的初始流修改为零流，然后在零流的基础上，利用最小费用流算法Ⅱ去求流值为A的最小费用流。如针对例9.19，可以先把图9.95的初始流修改为零流，然后再利用最小费用流算法Ⅱ求流值为7的最小费用流，这样求出的最小费用流和图9.100的结果一样。

特别提示

（1）针对运输网络，无论是最小费用流算法Ⅰ还是最小费用流算法Ⅱ，都可以先将给出的初始流修改为零流，然后在零流的基础上求解最小费用流。

（2）针对运输网络，有时求出的流值以及总的最小费用会一样，即最小费用流是一样的，但网络流的分布状态可能不同。

（3）最大流算法和最小费用流算法的最大区别是，最大流算法是寻找任意的增流链来调整分配流量，而最小费用流算法则是通过构建增流网络，然后来调整分配最小费用流。