前面已经讲过，在既定的网络中，需要知道能通过网络的最大流量是多少，即在遵循性质9.2（容量约束条件）和性质9.3（流量守恒条件）的前提下，使网络的流值Valf达到最大，从而最大限度地发挥网络的利用率。这就是网络的最大流问题，最大流问题也是图论的核心问题之一。

针对一个运输网络，分配流量的方案可能不止一个，即网络流f有多个。若f *是满足条件Val f *=max{Valf | f为G的一个流}的网络流，称网络流f *为运输网络G的最大流。

学习网络最大流的目的就是在遵从容量约束条件和流量守恒条件的前提下，通过一定的方法使网络的流量达到最大。

下面首先介绍相关概念，在此基础上，给出相关的定理和推论，然后学习最大流算法的思路和最大流算法的步骤。

1.相关概念

（1）基础概念。

如图9.51所示，给定网络图G的边e，设f为G上一个网络流，针对边e给出如下一些定义：

零边：若边的流量等于0，即f(e)=0，则称边e为网络流f的零边。

根据容量约束条件，零边意味着边的流量只能增加，不能减小，流量可以增加的最大量值为c(e)-f(e)，即为c(e)。

饱和边：若边的流量等于边的容量，即f(e)=c(e)，则称边e为网络流f的饱和边。

根据容量约束条件，饱和边意味着边的流量不能增加，只能减小，流量可以减小的最大量值为f(e)。

不饱和边：若边的流量小于边的容量，即f(e)<c(e)，则称边e为网络流f的不饱和边。

根据容量约束条件，不饱和边意味着边的流量既可以增加，也可以减小，流量可以增加的最大量值为c(e)-f(e)，流量可以减小的最大量值为f(e)。

正边：若边的流量大于0，即f(e)>0，则称边e为网络流f的正边。

正边有可能是饱和边，即f(e)>0，并且f(e)=c(e)；也有可能是不饱和边，即f(e)>0，并且f(e)<c(e)。反过来说，饱和边一定是正边，因为饱和边f(e)>0；不饱和边有可能是正边，如f(e)<c(e)，并且f(e)>0；也有可能是零边，如f(e)<c(e)，并且f(e)=0。

通过以上几个定义，可以知道哪类边的流量是可以增加的，哪类边的流量是可以减小的，同时也可以知道流量增加或减小的最大量值又是多少。

如图9.52中，零边v1v2的流量只能增加，可以增加的最大量值为6-0=6；既为不饱和边又为正边的v3v4，流量既可以增加也可以减小，流量可以增加的最大量值为6-4=2，流量可以减小的最大量值为4；既为饱和边又为正边的v5v6，流量只能减小，可以减小的最大量值为6。

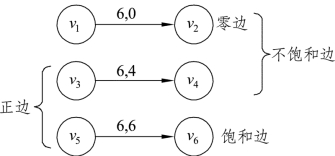
图9.52

设Q=x,v1,…,vi,u,v,vj,…,vk,t为G上网络流f的一条初等链，对初等链Q给定图形9.53所示：

图9.53

图9.51

针对链Q给出如下一些定义：

前向边：若链Q中有u到v的有向边(u,v)，则称边(u,v)为链Q的前向边。如图9.53中，边(vi,u)、(u,v)、(vk,t)为链Q的前向边。

后向边：若链Q中有v到u的有向边(v,u)，则称边(v,u)为链Q的后向边。如图9.53中，边(x,v1)、(v,vj)为链Q的后向边。

简言之，若边的方向与链的走向一致，则该边称为链的前向边；若边的方向与链的走向相反，则该边称为链的后向边。

给出前向边和后向边定义的目的，就是对网络图的流量进行调整和分配时，确定哪类边的流量需要增加，哪类边的流量需要减少。为了解决这个问题，下面给出一个性质。

性质9.4　给定初等链Q，在遵从容量约束条件的前提下，假设需要给初等链Q增加一定的流量l(Q)，把l(Q)称为链Q的调整量，则初等链Q中的前向边要加上调整量l(Q)，后向边要减去调整量l(Q)。

下面通过一个示例来理解性质9.4。

在一个具有可行流的网络图 G 中，假定有一条初等链 Q1=x,…,v3,v4,v5,…,y，如图9.54所示。针对中间点v4，接收的流量之和与发出的流量之和均为7，满足流量守恒条件。针对链Q1，边(v3,v4)是中间点v4接收流量的边，而边(v4,v5)是中间点v4发出流量的边。若给初等链Q1中的边(v3,v4)的流量增加2个，就会导致中间点v4接收的流量之和为9，为了满足流量守恒条件，中间点v4发出的流量之和也应该为9，所以需要把初等链Q1中的边(v4,v5)的流量增加2个，这样才能满足流量守恒条件，调整后如图9.55所示。而边(v4,v5)恰恰是初等链Q1的前向边，这就简单的解释了性质9.4中前向边要加上调整量的原因。

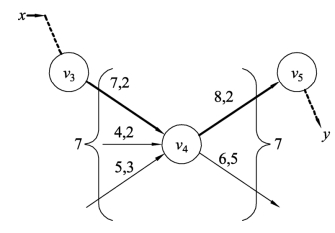
图9.54

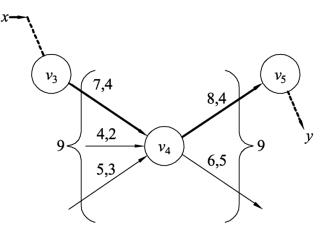
图9.55

同样，在一个具有可行流的网络图G中，假定有一条初等链Q2=x,…,v3,v4,v5,…,y，如图9.56所示。针对中间点v4来说，接收的流量之和与发出的流量之和均为8，满足流量守恒条件。针对链Q2，边(v3,v4)是中间点v4接收流量的边，边(v4,v5)也是中间点v4接收流量的边；若给初等链Q2中的边(v3,v4)的流量增加2个，就会导致中间点v4接收的流量之和为10，而中间点v4发出的流量之和仍为8，为了满足流量守恒条件，就需要把初等链Q2中的边(v4,v5)的流量减少2个，这样才能满足流量守恒条件，调整后如图9.57所示。而边(v4,v5)恰恰是初等链Q2的后向边，这就简单的解释了性质9.4中为何后向边要减去调整量的原因。

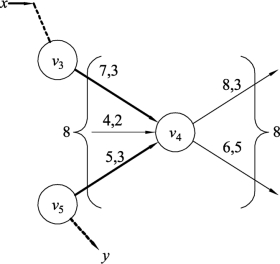
图9.56

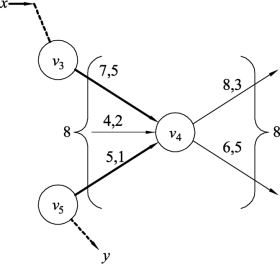
图9.57

特别提示

基于性质9.4可知，前向边的流量只能增加，后向边的流量只能减少，需要注意的是，如果前向边是饱和边，流量就无法增加，如果后向边是零边，流量就无法减少。

（2）核心概念。

在性质9.4中，提到初等链Q的调整量l(Q)，但如何确定l(Q)的大小并没有解决，下面首先给出确定调整量l(Q)大小的方法，然后给出几个核心概念。

给定网络图G中的一条初等链Q，同时设f为G上的一个网络流，针对初等链Q中的边e给定一个量值l(e)。由性质9.4可知，前向边的流量只能增加，后向边的流量只能减少，那么边e量值l(e)的大小可按照如下确定：

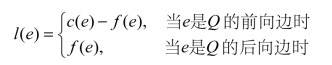
边的量值l(e)表明，若边e是前向边时，l(e)就是边的流量可能增加的最大量值；若边e是后向边时，l(e)就是边的流量可能减少的最大量值。

基于初等链Q中所有边的l(e)，初等链Q的调整量

l(Q)=min{l(e),e∈E(Q)}

这个公式说明，初等链Q的调整量l(Q)等于初等链Q中所有边的最小量值l(e)。

基于确定出的调整量l(Q)，其隐含的意义就是，若给整个链Q增加流量，则增加的量值最多是l(Q)，否则会造成某些边的流量大于容量，或造成某些边的流量为负值，从而违背了容量约束条件。依据确定出的调整量l(Q)，下面给出几个核心概念。

饱和链：当初等链Q的调整量l(Q)=0时，称初等链Q为网络流f的饱和链。

不饱和链：当初等链Q的调整量l(Q)>0时，称初等链Q为网络流f的不饱和链。

根据量值l(e)的定义及调整量l(Q)的确定方法，可以得出饱和链和不饱和链的性质：

性质9.5　若Q为网络流f的饱和链，则链Q中至少有一条前向边是饱和边，或至少有一条后向边是零边。

性质9.6　若Q为网络流f的不饱和链，则链Q中所有的前向边都是不饱和边，而且所有的后向边都是正边。

下面基于网络图9.58，对饱和链、不饱和链以及相关性质进行示例说明。

① 取链Q1=xx2v2x1v1，其中边(x,x2)、(x2,v2)、(x1,v1)为Q1的前向边，这些边的量值分别为

l(x,x2)=240-230=10，l(x2,v2)=130-100=30，l(x1,v1)=70-70=0

边(v2,x1)为Q1的后向边，其量值l(v2,x1)=50，则链Q1的调整量

l(Q1)=min{10,30,0,50}=0

这说明链Q1是饱和链，原因是链Q1中的前向边(x1,v1)为饱和边。

② 取链Q2=x2v3y2v1y1y，其中边(x2,v3)、(v3,y2)、(v1,y1)、(y1,y)为链Q2的前向边，这些边的量值分别为

l(x2,v3)=150-130=20，l(v3,y2)=120-30=90

l(v1,y1)=60-50=10，l(y1,y)=180-150=30

边(y2,v1)为Q2的后向边，其量值l(y2,v1)=20，则链Q2的调整量

l(Q2)=min{20,90,10,30,20}=10

这说明链Q2是不饱和链，原因是链Q2中所有的前向边都是不饱和边，而且后向边(y2,v1)是正边。

增流链：设f为网络图G的一个网络流，若初等链Q是一条从源x到汇y的不饱和链，则初等链Q称为网络流f的增流链。

显而易见，增流链一定是不饱和链，而不饱和链不一定是增流链，因为不饱和链必须同时包含源和汇才能称为增流链。如图9.58中的不饱和链Q2就不是增流链，因为它不包含源x。如果把不饱和链Q2加上边(x,x2)，即链Q3=(x,x2)+Q2，那么Q3既是不饱和链也是增流链。依据前面的相关概念以及调整量的确定公式等，针对网络图G中存在的网络流f，可以给出网络流量的调整公式：

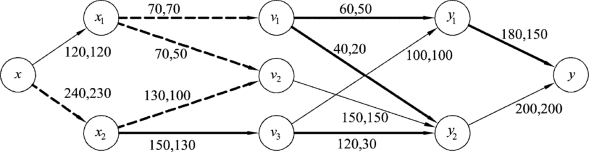
图9.58

利用调整公式（9.4），可以把一条不饱和的增流链调整为饱和链，进而使整个网络图的流量得到了提高，从而把网络的网络流f调整成一个新的网络流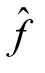，此时网络的流值Val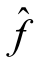=Val f+l(Q)。称新的网络流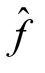为原有网络流f的基于Q的修改流。对于新的网络流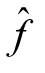而言，已经将不饱和的增流链Q调整为饱和链，那么链Q中至少有一条前向边变成了饱和边，或至少有一条后向边变成了零边。

在图9.58中，针对上面提到的链Q3=xx2v3y2v1y1y，前向边的量值分别为l(x,x2)=10，l(x2,v3)=20，l(v3,y2)=90，l(v1,y1)=10，l(y1,y)=30，后向边的量值为l(y2,v1)=20，调整量

l(Q3)=min{10,20,90,10,30,20}=10>0

则Q3是增流链。利用调整公式（9.4），把增流链Q3的所有前向边的流量加上10，把所有后向边的流量减去10，调整后的网络流如图9.59所示。

图9.59

图9.58中不饱和的增流链Q3，在图9.59中变成了饱和链，因为边(x,x2)、(v1,y1)变成了饱和边。在图9.58中，网络流f的流值Val f=350，而在图9.59中，新的网络流的流值，从而使整个网络图提高了10个流量。

由此可知，通过增流链可以判断网络图的流量状态，同时增流链也是调整流量的依据，即通过增加增流链的流量，来提高整个网络图的流量。

2.相关定理和推论

定理9.1　对于网络图G中任意一个网络流f和任意割K=(S,S*)，有

其中。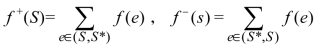

定理9.1表明，通过网络图G的任一横截面的净流值都为Valf，即Valf等于任意一个横截面的输入量与输出量的代数和。

定理9.2　对于网络图G中任意一个网络流f和任意割K=(S,S*)，有：

（1）Valf≤CapK；

（2）Valf=CapK的充要条件为：对任意的e∈(S,S*)，边e为f的饱和边；对任意的e∈(S*,S)，边e为f的零边。

定理9.2表明，G上任意一个网络流的流值不会超过任意割的容量，同时表明，若f为最大流，K为最小割，则二者是相等的。由此可以得出以下推论：

推论9.1　在网络图G中，最大流的流值和最小割的割值是相等的。

推论9.2　设f是网络图G的一个网络流，K是一个割，若Valf=CapK，则f为G的最大流，K是一个最小割。

定理9.3　网络流f为网络图G的最大流的充要条件是G中不存在f的增流链。

由此可以得出以下推论：

推论9.3　如果网络G中不含有网络流f的增流链，则网络流f为最大流。

推论9.4　如果网络G中含有网络流f的增流链，则网络的流值还可以增加。

特别提示

定理9.2以及由此得出的推论9.1、推论9.2，也称为最大流最小割定理。另外，可以得出一个求最小割的方法，即基于求出的网络图的最大流，把网络图从源或汇断开，即可得到一个最小割。

3.寻找增流链的方法

至此可以说，利用定理9.3或推论9.3、推论9.4，解决了如何判断网络的流量是否达到最大的问题，同时也可以利用调整公式（9.4），解决了如何增加网络流量的问题。

另外，前面也给出了增流链的定义，增流链定义的思路如下（见图9.60）：

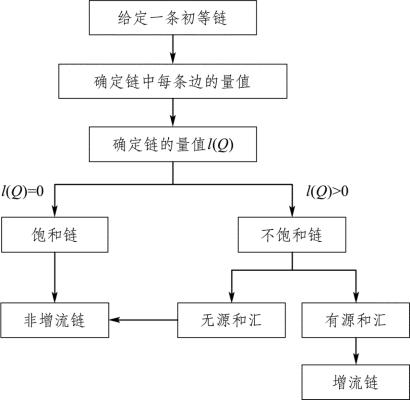
图9.60

由图9.60可知，增流链的定义只是用来判定某一条初等链是否为增流链的。

另外，定理9.3只是直观地观察网络图是否存在增流链，而对一个顶点较多的运输网络，要通过观察的方法来找出所有的增流链是相当不容易的，所以最大流问题还没有彻底解决，因为还没有解决如何在网络图中寻找增流链的问题。(www.daowen.com)

下面介绍在网络图中寻找增流链的方法——标号法。

用标号法寻找增流链的步骤：

第一步：对未检查的边(u,v)的顶点v进行标号，标号的方式为(u,边的方向,l(v))，其中标号的各个部分可如下确定：

（1）u：表示被标号点v的前一个顶点。

（2）边的方向：当被标号点v为终点时，即边(u,v)为前向边时，用“+”标示；当被标号点v为始点时，即边(u,v)为后向边时，用“-”标示。

（3）l(v)：当被标号点v为终点时，l(v)=min{l(u),c(u,v)-f(u,v)}；当被标号点v为始点时，l(v)=min{l(u),f(u,v)}。

另外，默认源x的标号为(0,+,+∞)。

第二步：继续检查，判断顶点v后面的边(v,z)能否成为增流链的边。边(v,z)若成为增流链中的边所具备的条件如下：

（1）如果边(v,z)是前向边，则应该有f(v,z)<c(v,z)。

由前面知识可知，前向边流量只能增加，所以边(v,z)不能是饱和边。

（2）如果边(v,z)为后向边，则必有f(v,z)>0。

由前面知识可知，后向边流量只能减少，所以边(v,z)不能是零边。

第三步：若边(v,z)能够成为增流链的边，就使顶点z成为被标号的点，再对被标号点z按照第一步的标号方式进行标号。

第四步：返回第二步，不断循环，直至找不到被标号点。如果汇y没有被标号，说明不存在增流链；如果汇y被标号，说明存在增流链，此时按照标号方式的第一项，从汇y逆向追踪，即可得到增流链Q，同时也可得到增流链Q的调整量l(Q)=l(y)，即调整量l(Q)的值为汇y标号的l(y)值。

标号法中标号方式的第一项“u”和第二项“边的方向”容易理解，关键是第三项“l(v)”值的确定，所以第一步中的第（3）点是标号法的核心。

为了更好地掌握和理解l(v)值的确定公式，下面以一个示例来解释l(v)值确定公式的合理性：

给定初等链Q1，如图9.61所示。按照调整量的定义，先确定边的量值，l(v1,v2)=6-2=4，则链Q1的调整量

l(Q1)=min{l(v1,v2)}=min{4}=4

现在用l(v2)表示l(Q1)，即l(v2)=l(Q1)=4，将l(v2)标示在顶点v2的旁边，标示如图9.61所示：

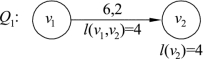
图9.61

给定另一初等链Q2，Q2=Q1+(v2,v3)，如图9.62所示。按照调整量的定义，确定边的量值，l(v1,v2)=6-2=4，l(v2,v3)=5-3=2，链Q2调整量

l(Q2)=min{l(v1,v2),l(v2,v3)}=min{4,2}=2

上式还可以写为

l(Q2)=min{l(Q1),l(v2,v3)}=min{l(v2),l(v2,v3)}=min{4,2}=2

现在用l(v3)表示l(Q2)，即l(v3)=l(Q2)=2，将l(v3)标示在顶点v3的旁边，标示如图9.62所示：

再给定另一初等链Q3，Q3=Q2+(v3,v4)，如图9.63所示。按照调整量的定义，确定这些边的量值，l(v1,v2)=6-2=4，l(v2,v3)=5-3=2，l(v3,v4)=4-1=3，那么链Q3的调整量就为

l(Q3)=min{l(v1,v2),l(v2,v3),l(v3,v4)=3}=min{4,2,3}=2

同样,上式还可以写为

l(Q3)=min{l(Q2),l(v3,v4)}=min{l(v3),l(v3,v4)}=min{2,3}=2

现在用l(v4)表示l(Q3)，即l(v4)=l(Q3)=2，将l(v4)标示在顶点v4的旁边，标示如图9.63所示：

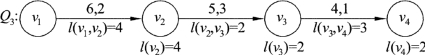
图9.63

通过以上过程，可以得出一个规律：一条衍生的初等链，在计算它的调整量时，不必按照调整量的定义，对每一条边的量值进行重复计算，而衍生初等链的调整量就是在原有初等链的调整量和新加边的量值中取最小值即可。

比如，在求出初等链Q2的调整量并在标示的基础上，可以直接计算出初等链Q3的调整量

l(Q3)=min{l(v3),l(v3,v4)}=min{l(v3),c(v3,v4)－f(v3,v4)}=min{2,4-1}=2

再给定另一初等链Q4，Q4=Q3+(v4,v5)，如图9.64所示。在上一过程已经知道l(v4)=2，边(v4,v5)为后向边，所以l(v4,v5)=f(v4,v5)=1，则有

l(Q4)=min{l(v4),l(v4,v5)}=min{2,1}=1

同样，现在用l(v5)表示l(Q4)，即l(v5)=l(Q4)=1，将l(v5)标示在顶点v5的旁边，标示如图9.64所示：

图9.64

通过以上分析，不但解释了l(v)值确定公式的合理性，也示例了标号的作用。

示例：给下面的网络图（见图9.65）进行标号。

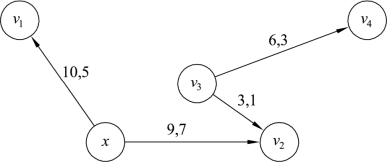
图9.65

首先给起点x标号为（0,+,+∞），边(x,v1)为前向边，l(x,v1)=10-5=5，则

l(v1)=min{l(x),l(x,v1)}=min{+∞,5}=5

对v1标号（x,+,5），顶点v1没有后续边，停止。边(x,v2)为前向边，l(x,v2)=9-7=2，则

l(v2)=min{l(x),l(x,v2)}=min{+∞,2}=2

对v2标号(x,+,2)。顶点v2有后续边，继续标号，边(v2,v3)为后向边，l(v2,v3)=1，则有

l(v3)=min{l(v2),l(v2,v3)}=min{2,1}=1

对v3标号(v2,-,1）。顶点v3有后续边，继续标号，边(v3,v4)为前向边，l(v3,v4)=6-3=3，则

l(v4)=min{l(v3),l(v3,v4)}=min{1,3}=1

对v4标号(v3,+,1)，顶点v4没有后续边，停止，至此全部标号完毕。标号结果如图9.66所示。

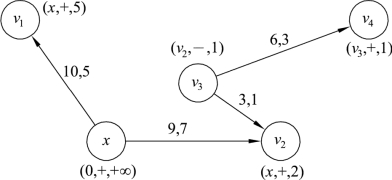
图9.66

4.最大流算法

利用定理9.3或推论9.3、推论9.4，解决了如何判断网络的流量是否达到最大的问题；同时可以利用调整公式（9.4），解决了如何增加网络流量的问题；另外，通过标号法也解决了如何在网络图中寻找增流链的问题。至此，可以给出网络图的最大流算法。

最大流的算法很多，这里主要介绍比较经典的Ford-Fulkerson算法。此算法是1956年由Ford提出，又由Fulkerson修改的最大流算法，算法的基本思路是利用标号法寻找增流链，然后在容量约束条件和流量守恒条件下，通过调整公式（9.4）给网络分配最大的流量。

（1）最大流算法思路。

给定网络图G一个初始的可行流f（也可以是零流），判断或寻找网络图G中有无关于网络流f的增流链，如果没有f的增流链，则当前的网络流f即为最大流；如果有f的增流链Q，则根据调整公式（9.4），得到f的基于Q的修改流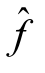，即Val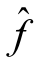=Valf+l(Q)，再将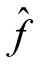视为网络流f，继续迭代，直到没有增流链为止。

（2）最大流算法。

给定一个具有初始流的（可行流或零流）的网络图G，最大流算法的过程如下：

第一步：给源x标号为(0,+,+∞)。

第二步：利用标号法寻找源x到汇y的增流链，若没有找到增流链，说明已经达到最大流，算法终止；若找到增流链，从终点汇y进行逆向追踪，即可得到增流链 Q 以及增流链的调整量 l(Q)，l(Q)=l(y)；再利用调整公式（9.4），对增流链Q所有前向边的流量都加上调整量l(Q)，所有后向边的流量都减去调整量l(Q)，从而得到新的网络流。

第三步：返回第二步。

5.最大流算法示例

下面通过一个例题说明最大流算法的具体过程。

例9.14　给定网络图9.67，边旁数据分别表示容量和流量，请分配最大流。

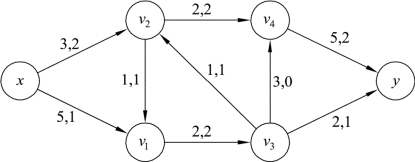
图9.67

解　第一步：首先给源x标号（0,+,+∞），如图9.68所示，此时源x是已经标号而未检查的点，其余都是未标识的点。

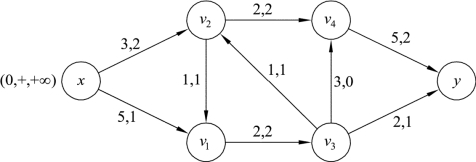
图9.68

第二步：在网络图G中，利用标号法寻找增流链，寻找增流链的过程如下：

（1）对源x进行检查，从x出发有前向边(x,v1)、(x,v2)，并且都为不饱和边，即f(x,v1)=1<c(x,v1)=5，f(x,v2)=2<c(x,v2)=3，所以顶点v1和v2都可以进行标号。任选一个点进行标号，这里选择顶点v1进行标号，

l(x,v1)=5-1=4，l(v1)=min{l(x),l(x,v1)}=min{+∞,4}=4，

对v1标号为(x,+,4)。此时源x已被检查过，在x标号下添加横线，如图9.69所示：

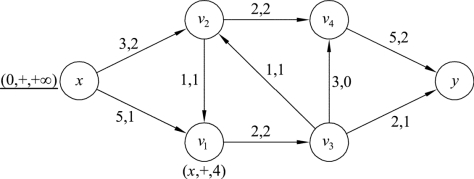
图9.69

（2）对v1进行检查，与v1有关的边(v1,v3)为前向边，但f(v1,v3)=c(v1,v3)=2，即边(v1,v3)为饱和边，所以v3不能标号。与v1有关的边(v1,v2)为后向边，且f(v1,v2)>0，有

l(v1,v2)=f(v1,v2)=1，l(v2)=min{l(v1),l(v1,v2)}=min{4,1}=1

对v2标号为(v1,-,1)。此时顶点v1已被检查过，在标号下添加横线，如图9.70所示：

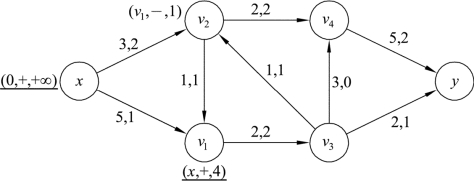
图9.70

（3）对v2进行检查，与v2有关的边(v2,v4)为前向边，其中f(v2,v4)=c(v2,v4)=2，即边(v2,v4)为饱和边，v4不能标号。与v2有关的边(v2,v3)为后向边，又f(v2,v3)>0，有

l(v2,v3)=f(v2,v3)=1，l(v3)=min{l(v2),l(v2,v3)}=min{1,1}=1

对v3进行标号(v2,-,1）。此时顶点v2已被检查过，在标号下添加横线，如图9.71所示：

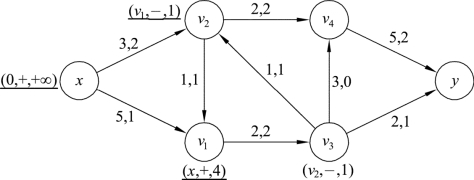
图9.71

（4）对v3进行检查，与v3有关的边有(v3,v4)、(v3,y)，有f(v3,v4)=0<c(v3,v4)=3，f(v3,y)=1<c(v3,y)=2，均为不饱和边，所以顶点v4和y都可以进行标号，可以任选一个点进行标号。这里选择顶点y进行标号，

l(v3,y)=2-1=1，l(y)=min{l(v3),l(v3,y)}=min{1,1}=1

对y进行标号(v3,+,1)。此时源v3已被检查过，在标号下添加横线，如图9.72所示：

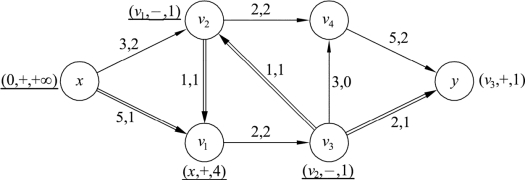
图9.72

因为汇y已经被标号，逆向追踪即可找到增流链Q，增流链Q如图9.72双箭头所示，同时得到调整量l(Q)=l(y)=1。

第三步：由图9.72可知，增流链Q=xv1v2v3y。对增流链Q所有前向边的流量都加上调整量l(Q)=1，所有后向边的流量都减去调整量l(Q)=1，结果如图9.73所示：

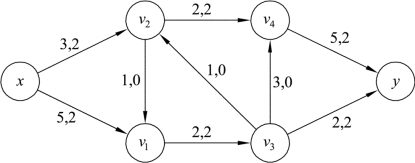
图9.73

第四步：返回第一步重新寻找增流链，针对图9.73，重复上述标号过程。先给源x标上(0,+,+∞），检查源x，给v1标号为(x,+,3）。检查v1发现后向边(v1,v2)的f(v1,v2)=0，所以v2不能标号；前向边(v1,v3)的f(v1,v3)=c(v1,v3)=2，所以v3也不能标号，此时说明v1后续边不能构成增流链。返回源x重新标记，给v2标号为(x,+,1）。检查v2，发现后向边(v2,v3)的f(v2,v3)=0，所以v3不能标记；前向边(v2,v4)的f(v2,v4)=c(v2,v4)=2，所以v4也不能标号。此时所有的顶点均不符合标号条件，标号过程无法进行，算法结束，标号结果如图9.74所示：

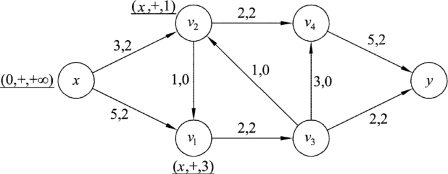
图9.74

在图9.74中不能找出增流链，所以图9.74分配的可行流即为该网络图的最大流，最大流量的流值为f(x,v1)＋f(x,v2)=f(v4,y)＋f(v3,y)=2+2=4。

特别提示

一个运输网络最大流的流值是一定的，但是最大流在网络中的分布状态是不同的，即最大流的分配方案可能多种多样。如例9.14第二步的（1）中，如果选择顶点v2进行标号，最后会得出最大流流值为4的另外一种分配方案；或在第二步的（4）中，选择顶点v4进行标号，也会得出最大流的流值为4的另外一种分配方案。