为了更形象地学习网络流的相关知识，下面给出一个引例。

例9.12　某运输企业计划对物资进行调运，已知出发地A1、A2分别有物资120吨和240吨，接收地B1、B2需要物资分别为180吨和200吨。运输线路如图9.40所示，其中F1、F2、F3为转运地，图中边旁的数字表示线路的运输能力。现在需要制定一个调运方案，使出发地A1、A2有尽可能多的物资调运到接收地B1和B2。

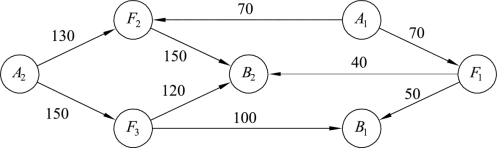
图9.40

以上问题其实是受线路输送能力的限制，也称为能力约束问题。

为了使图9.40更直观，把出发地A1、A2用x1、x2表示，接收地B1、B2用y1、y2表示，转运地F1、F2、F3用v1、v2、v3表示，同时按照如下思路作图9.40的同构图：把出发地放置在左边，接收地放置在右边，转运地放置在中间，同时把出发地具有的物资数用正号标在x1、x2旁，把接收地需要的物资数用负号标在y1、y2旁，如图9.41所示。

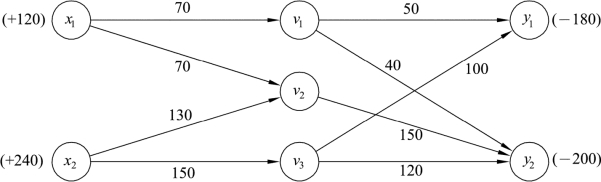
图9.41

针对此问题，不妨给出一个可行的具体调运方案，如表9.9所示：

表9.9　调运方案

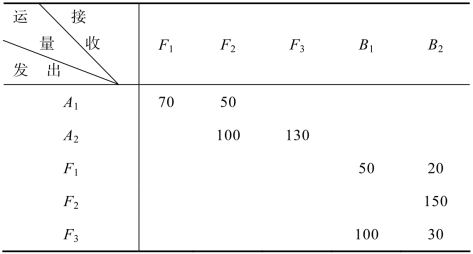
现在把以上调运方案的运量也标在网络图9.41中，如图9.42所示：

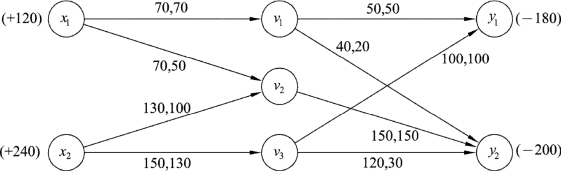
图9.42

1.基本概念

基于对例9.12中网络图的初步理解，给出如下定义：

给定有向图G=(V,E)，其中V=(v1,v2,…,vn)，E=(e1,e2,…,em)，针对边ei赋予两个非负的整数参数c(ei)、f(ei)，把c(ei)称为边ei的容量，有时把边(vi,vj)的容量写成cij；把f(ei)称为边ei的流量，有时把边(vi,vj)的流量写成fij；针对顶点集合V，取定两个非空子集X及Y，其中X∩Y=Ø，则称G=(V,E,C,F,X,Y)为运输网络，其中C为容量的集合，C=(c(e1),c(e2),…,c(em))；F为流量的集合，F=(f(e1),f(e2),…,f(em))；把X中的顶点x称为运输网络G的源；Y中的顶点y称为运输网络G的汇；I=V-(X∪Y)中的顶点为运输网络G的中间点；另外，把运输网络G的流量分布状态用f表示，f称为G的网络流。

在例9.12中的图9.42中，出发地x1、x2称为源，接收地y1、y2称为汇，转运地v1、v2、v3称为中间点，边旁表示运输能力和运量的数据分别称为容量和流量。

容量表示边所承载流量的最大能力，例如针对铁路网，边的容量可以表示区段间的最大通过能力；针对城市道路网，边的容量表示道路的通行能力。流量表示调运的分配方案，在不同的网络中所表示的内容也不一样，比如它可以表示实际中输送的物资量、道路上通过的车辆数（交通量）、网络中传送的信息量、水管中的水量等等。

特别提示

由定义可知，运输网络的源只发出流量，即源只有以它为起点的边，而没有以它为终点的边；汇只接收流量，即汇只有以它为终点的边，而没有以它为起点的边；中间点只转运流量，即中间点既有以它为起点的边又有以它为终点的边。

2.基本性质

针对一般运输网络的网络流分布，需要满足一定的条件，即对运输网络的流量进行分配时，需要遵从以下两个性质：

性质9.2　针对运输网络的任意一条边ei，均有0≤f(ei)≤c(ei)。

性质9.2说明，运输网络中每条边上的流量不超过该边承载流量的最大能力，即容量。此性质给出了边上流量的大小受限于该边的容量，所以性质9.2称为容量约束条件。

性质9.3　针对运输网络中任意一个中间点vi，vi∈I，定义f +(vi)为以vi为始点的所有有向边流量的函数和，f-(vi)为以vi为终点的所有有向边流量的函数和，则f+(vi)和f-(vi)满足f+(vi)＝f-(vi)。

性质9.3说明，运输网络中每一个中间点接收的流量之和等于发出的流量之和，这也是中间点只转运流量的体现。因为此性质给出了中间点的流量是守恒的，所以性质9.3称为流量守恒条件。

另外，针对整个运输网络来说，所有源发出的流量之和与所有汇接收的流量之和也应该是相等的，这也是运输网络调运方案的总调运量。

性质9.2和性质9.3给出的容量约束条件和流量守恒条件，是对运输网络分配流量时需要遵从的两个原则，把运输网络中符合上述性质的流称为可行流。图9.42的流量分布均遵从以上两个性质。

在任意一个运输网络中，至少存在一个可行流，因为对于每一个边ei，都可以定义f(ei)=0。显然，这个定义满足上述性质，把这个网络流f称为零流或平凡流。图9.41中并没有给出各边的流量，此时各边的流量可以默认为0，即图9.41所示的网络流为零流。

针对运输网络的网络流f，其流值用Valf表示，显然，Valf=f +(x)=f-(y)，其中x、y分别是源和汇。在图9.42中，调运总量为350吨，网络流f的流值Valf=f +(x)=f-(y)=350，即从出发地分别发出120吨和230吨，接收地分别接收150吨和200吨，在不同的运输线路上，有其各自的调运分量。

3.割及最小割

给定有向网络图G=(V,E)，设S是V的一个子集，其中源x∈S，再设子集S*=V-S，其中汇y∈S*；另记K=(S,S*)是起点在子集S中，终点在子集S*中的全部有向边的集合，即可表示为K={(u,v)|u∈S,v∈S*}，把边的集合K称为网络图G的一个割。把割K中所有边的容量之和称为该割的容量（也称为割值），用CapK表示。另外，把一个网络图G中割值最小的割K*称为最小割，即有CapK*=min{CapK|K为网络图G的一个割}。

例9.13　给定运输网络图9.43，边旁数据表示容量，试求不同的割及其容量。

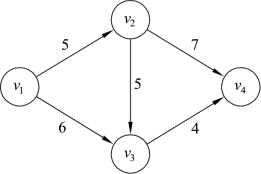
图9.43

(www.daowen.com)

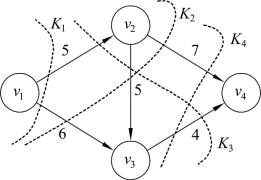
图9.44

针对图9.43，v1可以作为源，v4作为汇，下面通过表格9.10的形式，按照割的定义给出所有割、割中的边及其容量：

从表9.10可以看出，该运输网络的最小割为K3。

表9.10　割的列表

针对运输网络的割，从几何意义上解释就是，用一条割线将包含源的顶点和包含汇的顶点隔开，如例9.13中图9.44的虚线所示。

特别提示

如果把割的边从运输网络中移去，运输网络不一定分离成两部分，即不一定成为分割图，但是一定会把运输网络自源到汇的全部路都断开。也就是说，此时不能在运输网络上进行流的分配。所以从直观上可以理解为，运输网络上任意一个网络流f的流值Valf不能超过任意一个割的割值，即Valf≤CapK。

4.多源多汇运输网络的转换问题

基于实际问题所建立的运输网络，可能出现多个源或多个汇的情况，如例9.12的运输网络就有两个源两个汇。为了方便算法的运用，需要把多源多汇的运输网络转换为单源单汇的运输网络。

把多源多汇运输网络G转换为单源单汇运输网络G*的方法如下：

（1）在运输网络G中添加两个新的顶点x和y，分别成为G*的源和汇，G的顶点集合V成为G*的中间点集合。

（2）针对G中的源xi，用有向边(x,xi)连接顶点x和xi，边(x,xi)的容量视具体情况设定为+∞或某一具体的数值。

（3）针对G中的汇yi，用有向边(yi,y)连接顶点yi和y，边(yi,y)的容量视具体情况设定为+∞或某一具体的数值。

（4）设f是G上的一个网络流，按照如下方法定义G*上的网络流f *：

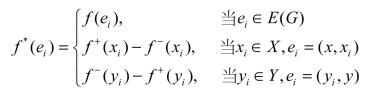
现在把例9.12的图9.42转换为单源单汇运输网络，如图9.45所示。

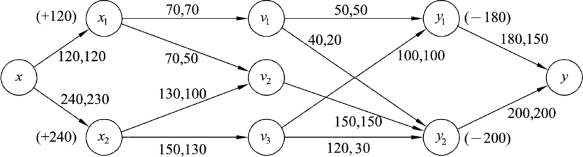
图9.45

在此示例的转换中，原有网络中的顶点、边以及边上的容量和流量在新的网络中没有变化，新添加的边(x,x1)，视具体情况x1处有物资120吨，容量设定为120；因为原有的源x1在新的网络图中成为中间点，按照流量守恒条件，边(x,x1)的流量就为120。同理，新添加的边(x,x2)的容量、流量也如此设定。针对新添加的边(y1,y)，视具体情况y1需要物资180吨，容量就设定为180；因为原有的汇y1在新的网络图中成为中间点，按照流量守恒条件，边(y1,y)的流量就为150。同理，新添加的边(y2,y)的容量、流量也如此设定。

另外需要说明的是，针对无源无汇的运输网络，转换为单源单汇运输网络时，新的源和汇可任意设定。如图9.46是无源无汇的运输网络，可以转换为图9.47的单源单汇运输网络，也可以转换为图9.48的单源单汇运输网络：

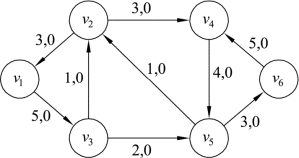
图9.46

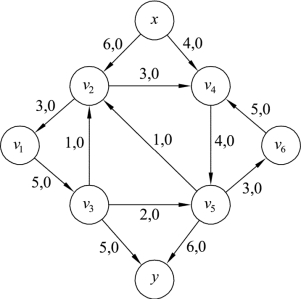
图9.47

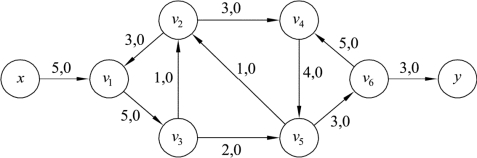
图9.48

当然，图9.46还可以转换成其他形式的单源单汇运输网络，但需要注意的是，转换为不同形式的单源单汇运输网络后，在分配流量时，网络流的方案可能不同。

5.顶点有容量约束的运输网络转换问题

在前面提到的运输网络中，对边给出了容量，但在实际问题中，往往顶点也具有容量。例如，针对铁路网，顶点所表示的车站也有接发能力的限制；针对城市道路网，顶点所表示的交叉口也有交叉口通行能力的限制。这就需要对运输网络的顶点给出容量。在对运输网络分配流量时，可能受到顶点容量的约束，为了方便分配流量，可将顶点的容量转换为边的容量。转换的方法是：对运输网络中有容量约束的顶点v，可以将该顶点拆分为v与v′两个顶点，原网络中以v为终点的边，仍然与顶点v连接，以v为起点的边，使其与顶点v′连接，令新边(v,v′)的容量等于原来顶点v的容量，这样就可以把顶点有容量约束的运输问题，转换为只有边有容量约束的运输网络。

其实这种转换方法从直观上也可以理解为把点拉长，从而使点变成了直线。例如，在图9.49中，顶点v3的容量为4，按照上面的方法可以将图9.49转换为图9.50。

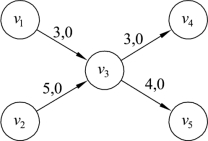
图9.49

图9.50