“一个邮递员每次送信，从邮局出发，必须至少一次地走过他负责投递范围的每一条街道，完成投递任务后再回到邮局。问他如何选择一条投递路线，使他所走的路程最短?”这个问题是我国管梅谷在1962年首先提出，所以称为中国邮路问题。

例如，图9.39为一街道示意图，每条边有一个权表示街道长度。如果v1是邮局所在点，邮递员需从v1出发，走遍每条街道递送邮件，最后再回到v1，他应选择什么路线才能使总的路程长度最短？

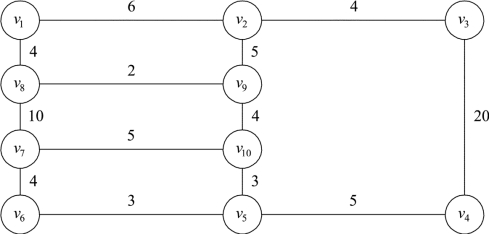
图9.39

中国邮路问题现象在现实中很多，如警察巡查街道、农民巡视农田等问题就是中国邮路问题，或称中国邮递员问题。

1.中国邮路问题的数学描述

给定一个连通的无向网络图G=(V,E,W)，所有边(vi,vj)的权wij>0，现在要求每条边至少通过一次的闭链Q，使得总权最小。如果图G恰好是欧拉图，那么从邮局出发，恰好每边走一次可回到邮局，这时总权必定最小；如果图G不是欧拉图，则某些边必然要重复走，当然要求重复走过的边的总长度最小。

2.中国邮路问题的一个算法

中国邮路问题的算法很多，不过大多是用奇偶点图上作业法来解决此问题，但该方法要验算每一个回路，计算量相当大，显得很不方便。这里主要介绍参考文献[2]中的另外一种比较有效的方法。算法思路如下：

第一步：若网络图G是一个欧拉图，即没有奇阶点（奇阶点指与点连接的边的数量为奇数），则该图可以一笔画出全部的边而无重复，此时，邮递员的最优路线就是一个欧拉环游，其总的行走长度为全部边长之和。但一般而言，街道图并非欧拉图，所以可以采用以下办法消除奇阶点，从而将非欧拉图变为欧拉图：

（1）找出全部奇阶点（全部奇阶点的顶点个数一定是偶数个）。

（2）将2m个奇阶点构成m个奇阶点对，使每点都在一个点对中，找出每个点对中两个奇阶点之间的一条链；对应于链上的每条边都添加一条长度和该边相等的边，经过添加边的两点间的街道，邮递员需要两次经过。

现在的问题是，奇阶点怎样两两匹配，各匹配点对之间取哪条链将使添加边的总长度最短，或使邮递路线的总长度最短。无需证明便可指出，最优解中奇阶点对之间的添加链应为最短路，因此，首先用最短路算法找出全部奇阶点任一点对间的最短路，然后据此寻找点与点的最优匹配。求最短路问题这里不做讨论。

第二步：解奇阶点匹配问题最优解的分枝定界算法。设au,v为奇阶点u至奇阶点v的最短路长度，将全部2m个奇阶点的最短路长度构成一个2m×2m矩阵：

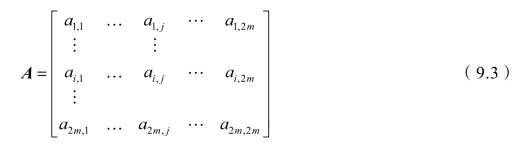
将A视为一个指派问题的费用矩阵，并令主对角线各元素等于∞，现在，对这个指派问题求解，最优解用2m个表中位置表示。

如果最优解在表中是关于主对角线对称（称为对称解），则这个角的右上角即为奇阶点匹配问题的最优解；如果指派问题最优解不是对称解，则解中必然存在由n个表位（n>2）构成的下标回路。例如，这样三个表位就构成一个下标回路：(1,3)、(3,5)、(5,1)。为了寻求对称解，这个回路必然打破，因此，可分别令表中这n个位置上的元素等于∞，将指派问题分枝成n个子问题，继续用指派问题的算法，计算出各子问题的目标值，并作为该子问题以后分枝的目标下界。这样不断分枝下去，直至没有任何一个子问题需要再分枝，即可确定奇阶点匹配问题的最优解。

任一子问题停止分枝的条件是：

（1）该子问题的解为对称解；

（2）其目标下界大于等于某一具有对称解的子问题的目标值。

计算步骤如下：

（1）找出全部奇阶点，用最短路算法计算全部奇阶点任一点对间的最短路长度。

（2）将奇阶点最短路长度矩阵A视为指派问题的费用矩阵，构成一个指派问题，形成初始子问题矩阵后，将某些不可能进入奇阶点匹配问题最优解的表位排除掉：

① 如果点i至点j的最短路由3个以上奇阶点组成，那么令ai,j=∞，aj,i=∞；

② 检查所有3奇阶点最短路，设为i—j—k，如果其中间点j与任何其他奇阶点构成的最短路都包含一个端点i或k，则令它们在初始子问题表中的元素ai,k=∞，将该问题置入待分枝子问题集合B，令奇阶点匹配问题的候选最优解目标T=∞。

（3）如果B为空，则停止计算，候选最优解S即为最优解；如果B非空，则从B中取出一个子问题k，用指派问题算法解子问题k。其目标值为Tk，解为Sk（以分配的表位集合表示）。

（4）若Tk ＞T，则停止分枝，转第三步取另一子问题，否则转第五步。(www.daowen.com)

（5）若Sk关于主轴对称，停止分枝，令候选最优解等于子问题k的解，令S=Sk，T=Tk，然后转第三步取另一个子问题；若Sk为非对称解，转第六步。

（6）在Sk中找出一个点数为n的下标回路(i1,j1)、(i2,j2)、…、(in,jn），其中i2=j1,i3=j2,…,in=jn-1，而且n>2，分别令子问题k的矩阵Ak中的，构成n个子问题，并置入待分枝子问题集合B，然后转第三步。

一般而言，采用分枝定界法解决一个邮路问题，计算量往往随问题规模的增大而急剧增大，本算法由于采用效率极高的指派问题算法，并对初始子问题作了简化处理，加速了问题向最优解的收敛，这对于解决一般的实际最短邮路问题，已经足够了。

3.中国邮路问题应用示例

例9.11　求图9.39所示的最短邮递路线。

解　图9.39有6个奇阶点，其对应的奇阶点之间的最短路矩阵如下：

针对上述A矩阵，按照指派问题求解思路求对应的最优解，最优解矩阵如下所示：

指派问题的解不对称，从而相对应的中国邮路问题的解不可行。解中存在如下下标环(1,4)、(4,5)、(5,1)，现在分别将A矩阵中下标环中3个位置及其对称位置的数值置为∞，从而构造出以下3个子问题。

子问题1：将A矩阵中(1,4)和(4,1)处的元素置为∞，构造出如下指派问题：

子问题1的最优解矩阵如下所示：

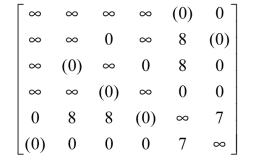
最优解不对称，子问题1的解不可行，最优目标函数值为36。

子问题2：将A矩阵中(4,5)和(5,4)处的元素置为∞，构造出如下指派问题：

子问题2的最优解矩阵如下所示：

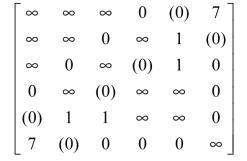
最优解对称，子问题2可行，最优目标函数值为36，添加边方案：7-8、2-9、5-1，添加边总长18。

子问题3：将A矩阵中(5,1)和(1,5)处的元素置为∞，构造出如下指派问题：

子问题3的最优解矩阵如下所示：

最优解对称，子问题3可行，最优目标函数值为36，添加边方案：5-6-7、8-9、2-9-10，添加边总长18。

由停止分枝的条件可知，子问题都不再往下分枝，已得到此中国邮路问题的最优解，子问题2或子问题3都是该问题的最优解。