在第9.1.4节中，介绍了基于图的树以及生成树问题，针对具有权的网络，常常需要寻找基于权之和最小的生成树，这就是最小生成树问题。

研究最小生成树问题具有一定的实用意义，如常常需要以最短线路连接网络中若干个固定点，例如城市水网铺设、交通网规划、煤气管网建设等等。为了便于维护、管理，这些都涉及线网中总长度最短的问题，而这些问题需要在线网中找出一棵最小生成树。类似的问题还有：如何设计总长度最小的公交网或公路网把若干城镇连接起来等等。也就是说，许多网络问题会派生出最小生成树问题，因此，最小生成树问题也是网络极值的基本问题之一。

下面的示例就是在网络图中找出一棵最小生成树问题。

例9.10　图9.38的点表示10个居住小区，边表示小区之间道路连接以及距离情况，问题是如何开通一条连接所有小区并使运行总路程最短的公交线路。

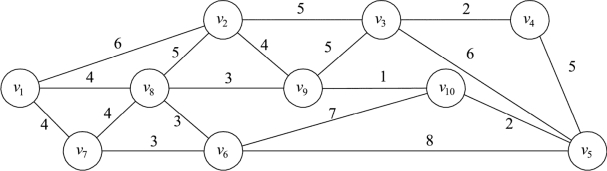
图9.38

1.最小生成树的数学描述

给定无向网络图G=(V,E)，其中V=(v1,v2,…,vn)，E=(e1,e2,…,em)，针对边ei的实数权为w(ei)，令T是G的生成树，则生成树T的权之和为

(www.daowen.com)

若T*也是G的生成树，并且有W(T*)=min{W(T)|T是G的一个生成树}，则称T*是无向网络图G的最小生成树。

2.寻找最小生成树的方法

在第9.1.4节中，已经介绍了针对图寻找生成树的两种方法，即破圈法和避圈法。针对具有权的网络图，寻找最小生成树的方法仍然是基于破圈法和避圈法的思路，但需要考虑权的大小问题。

下面给出在网络中寻找最小生成树的破圈法和避圈法的思路。

（1）避圈法。

在连通的无向网络图G中，从所有边中选出一条权最小的边，并把它纳入树中；在G中余下的边中再选择一条权最小且与选进树中的边不构成回路的边，同样将其纳入树中；如此反复，直到找不出这样的边为止。

（2）破圈法。

在连通的无向图G中，任取一个回路，将该回路中权最大的边去掉；如果回路中含有两条及两条以上权最大的边，则任取一条，再在余下的回路中重复这一步骤，直到图G中不含有回路为止。