在实际问题中，经常会遇到运输管理、管道铺设、交通网优化、物流调配、费用（成本）核算、工程进度等问题，这就需要解决出行距离最小、花费成本最低、距离最短、最优路径等一系列网络图的寻优问题。对这些类似问题，可以用“最短路径”来表述，有时简称为最短路。

最短路问题是图论的核心问题之一，也是网络规划的一个基本问题，无向网络和有向网络都有对应的最短路径问题。

所谓最短路，是指从网络中一点寻求到其他点的最短的路。具体什么是最短路，简单地说，最短路就是从网络中某一点到另外一点的所有路中，所有边的权的代数和最小的路。把路中所有边的权的代数和称为路长。

如果用P表示网络中从点vs到点vt的一条路，用W(P)表示该路的路长，若P*也为网络中从点vs到点vt的路，并且满足W(P*)=min{W(P)|P为网络中从点vs到点vt的路}，则P*为点vs到点vt路的最短路。

为了对最短路有更具体和更形象的认识，下面给出一个例题。

例9.8　假设图9.27为规划论证的某一城市区域内可以开通公交的公交线网，顶点表示停靠站，边表示道路，边旁数据表示道路长度，某公交公司准备在起始站v1和终点站v8之间开通一条距离最短的公交线路，现在需要确定这条公交线路的走向。

图9.27

针对此问题最容易想到的求解思路就是，设法把从v1到v8的所有路都找出来，然后再计算每条路中关于边的权的代数和即路长，最后取路长最小的路作为所求的最短路，即有如下过程：

路v1→v2→v5→v6→v8，其长度为1+5+7+1=14；

路v1→v2→v4→v6→v8，其长度为1+3+3+1=8；

路v1→v2→v5→v4→v6→v8，其长度为1+5+6+3+1=16；

………………………………

路v1→v3→v7→v8，其长度为4+2+2=8；

路v1→v3→v7→v6→v8，其长度为4+2+2+1=9。

通过比较可以知道，最短路为v1→v2→v4→v6→v8和v1→v3→v7→v8，路长为8，即可以按照v1→v2→v4→v6→v8或v1→v3→v7→v8的走向开通一条距离最短的公交线路。

例子9.8的求解采用的是全枚举法，这种方法虽然很明了，但过程繁琐，而且容易出错，尤其是对一些稍微复杂的网络，这样的算法几乎很难实现。因为点或边很多的网络，网络中的路会很多，而且在现实中遇到的网路几乎都是相对复杂的网路，所以需要有更方便、简洁的算法求最短路问题。

最短路的求解算法很多，主要有Dijkstra算法、Bellman-Ford算法以及SPFA算法等等，这些算法是许多更深层算法的基础。目前，使用比较普遍而且得到公认的经典算法是E.W.Dijkstra在1959年提出的最短路求解算法，简称为Dijkstra算法。这个算法的另外一个特点就是，不仅能求出某点到另外一点的最短路，也能求出某点到网络中其他各个点的最短路。下面对Dijkstra算法的相关内容进行介绍。

1.Dijkstra算法思想

性质9.1　在网络图G中，假设从顶点v1到顶点vn的最短路径P为v1…vi…vn，那么从v1沿着路径P到vi的路径P1也是v1到vi的最短路。也就是说，P不仅是起点v1到终点vn的最短路，而且由v1到路径P上任意一个中间点vi的最短路P1也在路径P上。

论证　如图9.28所示，设从vi沿着路径P到vn的路径为P2，则有

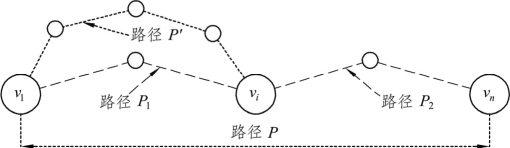
图9.28

W(P)=W(P1)+W(P2)

利用反证法。反设从v1到vi的最短路不是路径P1，而是另外一条路径P′，即有W(P′)＜W(P1)，则有

W(P′)+W(P2)＜W(P1)+W(P2)

此时出现　W(P′)+W(P2)＜W(P)

这说明从v1到vn的最短路不是路径P，而是P′与P2组成的路径，这与从v1到vn的最短路径是P的前提相矛盾。

由以上性质可以想到，为了求由v1到vn的最短路径，可以先求出v1到网络中间点的最短路，然后再逐步扩展到终点vn，由此，Dijkstra算法的思想如下：

在最短路的计算过程中，为了将已经求出最短路的点与尚未求的点分开，可以针对顶点给出两个子集合S和T，已经求出最短路的点置于集合S中，其他点置于集合T中。开始时把起点v1置于集合S中，把其他点置于集合T中；随着最短路计算过程的推移，集合S中的点逐渐增多，集合T中的点逐渐减少，当终点vn也被纳入到集合S中时，计算结束。为了便于计算和区分各个顶点是否已进入集合S中，需要对已求出最短路的点vj赋以标号，这个标号由两部分组成，记为(d(v1,vj),vi），其中d(v1,vj)是从起点v1到vj的最短路的路长，vi是起点v1到vj的最短路中vj的前一个顶点。

因为Dijkstra算法需要标号，所以也称为标号法，又因为标号中包含两部分，所以也称为双标号法。

2.Dijkstra算法步骤

给定一个网络G=(V,E)，这里用wij表示网络中边(vi,vj)的权，v1是网络的起点，vn是终点，vi、vj等是网络的中间节点，其中i，j=2,3,…,n-1且i≠j，设子集合S和T，S=Ø，T=V={v1,…,vn}。

再设L(v1,vi)表示起点v1到点vi的当前最短路的路长，可以把L(v1,vi)简写为L(vi)；同样，L(v1,vj)表示起点v1到点vj的当前最短路的路长，也把L(v1,vj)简写为L(vj)；L(vi)+wij是从起点v1出发，到点vi的最短路，再经由vi后到点vj的路长。那么L(vj)=min{L(vi)+wij；L(vj)}就是从起点v1到点vj的两条路径中，选择最短的一条作为起点v1到点vj新的最短路的路长。

图9.29为前面相关界定的简单的图形解释。

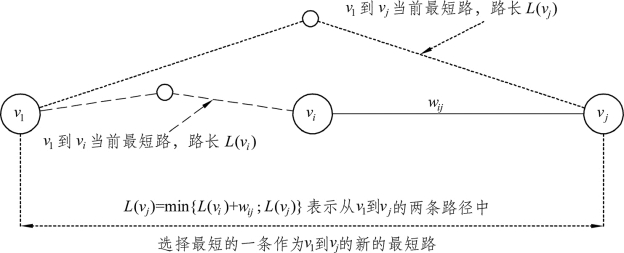
图9.29

由Dijkstra算法思想及前面的相关界定，求v1到vn最短路的Dijkstra算法步骤如下：

第一步：设L(v1)=0，L(vi)=+∞，其中i=2,…,n。在网络图中，把起点v1赋以标号(L(v1),v1)，即（0,v1），其余各点均标为(+∞,v1)。

第二步：检查起点v1，即将网络中v1的标号变为(0*,v1)，表示v1已被检查，同时设集合S={v1}，T={v2,…,vn}。

第三步：针对其他点vi，若v1与vi没有直接连线，vi的标号就保持不变；若v1与vi有直接连线，则点vi的标号就变为(L(vi),v1)，其中

L(vi)=min{L(v1)+W1i；L(vi)}=min{0+W1i；+∞}=W1i

第四步：计算L(vi)*=min{L(vi),其中vi∊T}。将L(vi)*对应点vi的第一个标号L(vi)标上*，即变为L(vi)*，表示vi已被检查，同时设集合S={v1,vi}，此时vi∉T。

第五步：再依次求vj，若vi与vj没有直接连线，vj的标号就保持不变；若vi与vj有直接连线，则计算L(vj)=min{L(vi)+Wij；L(vj)}。若L(vj)来源于L(vi)+Wij，则把vj的标号修改为(L(vi)+Wij,vi），否则点vj的标号保持不变。

第六步：计算L(vj)*=min{L(vj),其中vj∊T}。将L(vj)*对应点vj的第一个标号L(vj)标上*，即变为L(vj)*，表示vj已被检查，同时设集合S={v1,vi,vj}，而vj∉T。

第七步：返回第五步，直到所有的点都被检查，而且终点vn进入到集合S中为止。

第八步：在网络中，从终点vn的第二个标号开始反向追踪，从而找出最短路径；同时从终点vn的第一个标号可以读出起点v1到终点vn最短路的路长。另外，从各个点的第一个标号也可以读出从起点v1到该点的最短路路长。

3.最短路算法应用示例

例9.9　针对例9.8的网络，用dijkstra算法求点v1到点v8的最短路。

解　具体解题步骤如下：

第一步：设L(v1)=0，L(vi)=+∞，其中i=2,…,8。在网络中，把起点v1赋以标号（L(v1),v1），即（0,v1），其余各点均标为(+∞,v1），检查起点v1，并将网络中v1的标号变为(0*,v1），同时设集合S={v1}，T={v2,…,v8}，如图9.30所示：

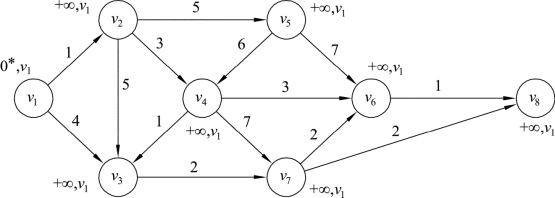
图9.30

将此过程列成表格，如表9.1所示。

表9.1　第一步计算结果

第二步：v1与v2、v3有直接连线，则

L(v2)=min{L(v1)+W12；L(v2)}=min{0+1；+∞}=1

点v2的标号变为(1,v1）。同理

L(v3)=min{L(v1)+W13；L(v3)}=min{0+4；+∞}=4

点v3的标号变为(4,v1），其余点的标号保持不变。再计算：

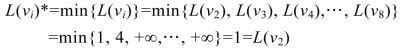
将网络中v2的标号变为（1*,v1），同时设集合S={v1,v2}，此时v2∉T，如图9.31所示。同时将表格9.1扩展为表9.2。

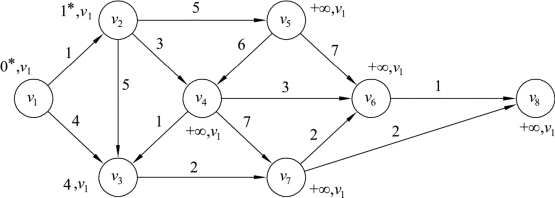
图9.31

表9.2　第二步计算结果

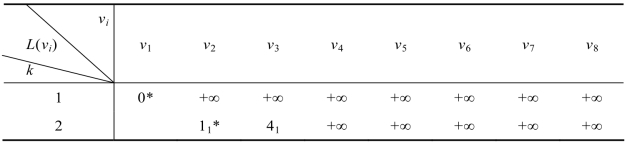
第三步：从v2开始继续检查，v2与v3、v4、v5有直接连线，(www.daowen.com)

L(v3)=min{L(v2)+W23；L(v3)}=min{1+5；4}=4

点v3的标号保持不变；

L(v4)=min{L(v2)+W24；L(v4)}=min{1+3；+∞}=4

点v4的标号变为(4,v2）；

L(v5)=min{L(v2)+W25；L(v5)}=min{1+5；+∞}=6

点v5的标号变为（6,v2），其余点的标号保持不变。再计算：

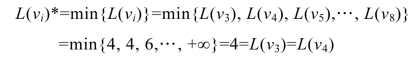
对最小值L(v3)和L(v4)可以任意取一个，这里取L(v3)作为最小值，将网络中v3的标号修改为（4*,v1），同时设集合S={v1,v2,v3}，此时v3∉T，如图9.32所示。同时将表格9.2扩展为表9.3。

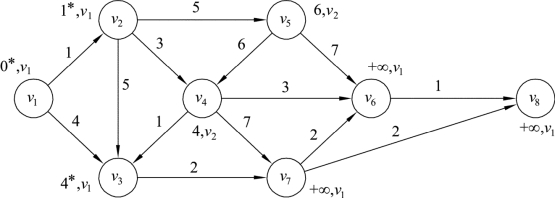
图9.32

表9.3　第三步计算结果

第四步：从v3开始继续检查，v3与v7有直接连线，

L(v7)=min{L(v3)+W37；L(v7)}=min{4+2；+∞}=6

点v7的标号变为（6,v3），其余点的标号保持不变。再计算：

将网络中v4标号改为(4*,v2），设集合S={v1,v2,v3,v4}，此时v4∉T，如图9.33所示。同时将表格9.3扩展为表9.4。

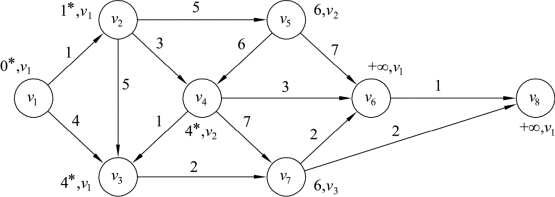
图9.33

表9.4　第四步计算结果

第五步：从v4开始继续检查，v4与v3、v6、v7有直接连线，

L(v3)=min{L(v4)+W43；L(v3)}=min{4+1；4}=4

点v3的标号保持不变；

L(v6)=min{L(v4)+W46；L(v6)}=min{4+3；+∞}=7

点v6的标号变为(7,v4）；

L(v7)=min{L(v4)+W47；L(v7)}=min{4+7；6}=6

点v7的标号保持不变，其余点的标号保持不变。再计算：

这里取L(v7)作为最小值，可将网络中v7的标号修改为(6*,v3），同时设集合S={v1,v2,v3,v4,v7}，此时v7∉T，如图9.34所示。同时将表格9.4扩展为表9.5。

图9.34

表9.5　第五步计算结果

第六步：从v7开始继续检查，v7与v6、v8有直接连线，

L(v6)=min{L(v7)+W76；L(v6)}=min{6+2；7}=7

点v6的标号保持不变；

L(v8)=min{L(v7)+W78；L(v8)}=min{6+2；+∞}=8

点v8的标号变为(8,v7），再计算：

L(vi)*=min{L(v5),L(v6),L(v8)}=min{6,7,8}=6=L(v5)

将网络中v5的标号修改为(6*,v2），同时设集合S={v1,v2,v3,v4,v7,v5}，此时v5∉T，如图9.35所示。同时将表格9.5扩展为表9.6。

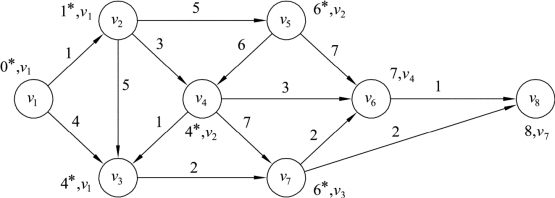
图9.35

表9.6　第六步计算结果

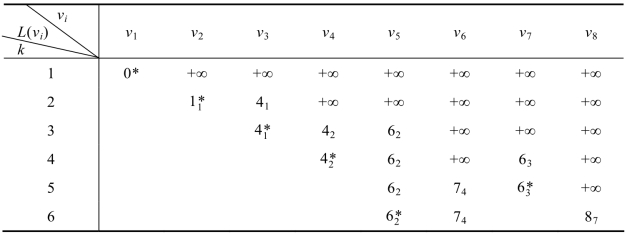
第七步：再从v5开始继续检查，v5与v6有直接连线，

L(v6)=min{L(v5)+W56；L(v6)}=min{6+7；7}=7

点v6的标号保持不变。再计算：

L(vi)*=min{L(v6),L(v8)}=min{7,8}=7=L(v6)

将网络中v6的标号变为(7*,v4），同时设集合S={v1,v2,v3,v4,v7,v5,v6}，此时v6∉T，如图9.36所示。同时将表格9.6扩展为表9.7。

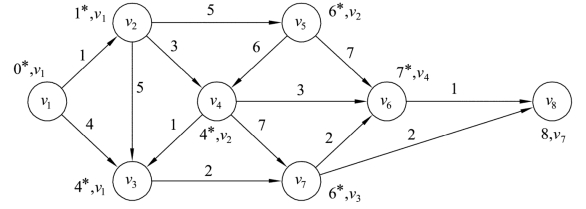
图9.36

表9.7　第七步计算结果

第八步：从v6开始继续检查，v6与v8有直接连线，最小值8来自两处，点v8的标号应该为(8,v6)和(8,v7），点v8的标号写为(8,v6v7）。再计算：

L(v8)=min{L(v6)+W68；L(v8)}=min{7+1；8}=8

L(vi)*=min{L(vi)}=min{L(v8)}=min{8}=8=L(v8)

将网络中v8标号变为（8*,v6v7），同时设集合S={v1,v2,v3,v4,v7,v5,v6,v8}，此时v8∉T，如图9.37所示。同时将表格9.7扩展为表9.8。

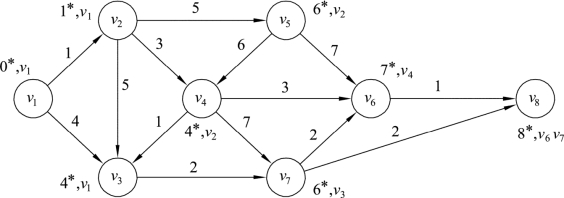
图9.37

表9.8　第八步计算结果

此时终点v8已经被标识和检查，算法结束。从终点v8的第一个标号可以读出起点v1到终点v8最短路的路长为8，同时从终点v8的第二个标号开始反向追踪，找出最短路径为v1→v2→v4→v6→v8和v1→v3→v7→v8，此网络有两条最短路。

另外，同样也可以读出从起点v1到该网络中任意一点的最短路及路长。

特别提示

（1）网络中的最短路不止一条时，要注意进行多点标号，如上例的第八步。另外，上例是利用dijkstra算法对有向网络寻找最短路，对无向网络时，其使用原理也一样。

（2）dijkstra算法只适用于网络中所有边的权Wij≥0的情况，当网络中出现负权边的时候，dijkstra算法就不能保证得到正确的结果。针对含有负权边求最短路的算法很多，但因这类问题算法的复杂性较高，本教材不作介绍。