图可以用几何的形式存储到计算机系统中，但计算机针对图的运用及决策，会面临数据计算的问题，这就涉及数据和图之间的转换处理。即把图转换为数据的形式，然后存储到计算机系统中，反之，可以把计算机系统中的数据转换成几何形式的图形，而矩阵就是数据和图互换时比较可用的方式。

无论是无向图还是有向图，都可以用关联矩阵或邻接矩阵的形式表示出来。有了关联矩阵和邻接矩阵，就可以把图以数据的形式存储在计算机系统中，反过来，也可以根据计算机系统中的数据矩阵，按照一定的方法把图绘制出来。

下面分别介绍无向图和有向图的关联矩阵和邻接矩阵的表示方法。

1.无向图的矩阵表示

（1）无向图的关联矩阵。

针对有m条边n个顶点的无向图G，G=(V,E)，其中V=(v1,v2,…,vn)，E=(e1,e2,…,em)，给定一个n行m列矩阵A=(aij)n×m，在矩阵外的左侧对应每一行依次标上n个顶点，在矩阵外的上侧对应每一列依次标上m条边，形式如下所示：

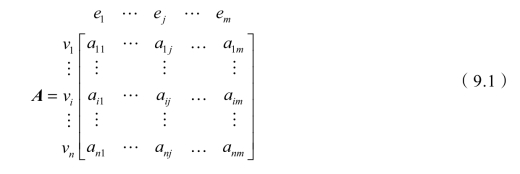
其中矩阵A中的元素aij按照如下确定：

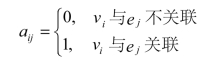
矩阵A称为无向图G的关联矩阵，关联矩阵刻画了无向图G的顶点与边的关联关系。

例9.4　写出图9.22的关联矩阵。

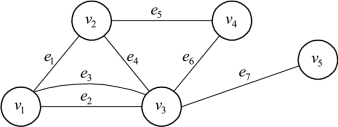
图9.22

解　图9.22的关联矩阵如下：

通过图9.22的关联矩阵，可以观察出无向图关联矩阵的特点：

① 第i行中1的个数是与顶点vi相连接的边的数量。

② 第j列中1的个数恒为2，因为每条边只有2个端点。

（2）无向图的邻接矩阵。

针对有m条边n个顶点的无向图G，G=(V,E)，其中V=(v1,v2,…,vn)，E=(e1,e2,…,em)，给定一个n行n列矩阵A=(aij)n×n，在矩阵外的左侧对应每一行依次标上n个顶点，在矩阵外的上侧对应每一列依次标上n个顶点，形式如下所示：

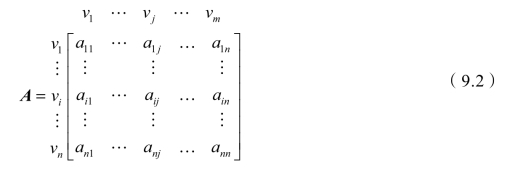
其中矩阵A中的元素aij为连接顶点vi和顶点vj的边的数量。把矩阵A称为无向图G的邻接矩阵，邻接矩阵刻画了无向图G的顶点之间边的连接数量情况。

例9.5　写出图9.22的邻接矩阵。

解　图9.22的邻接矩阵如下：

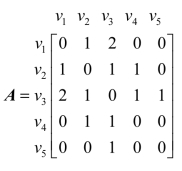
通过图9.22的邻接矩阵，可以观察出无向图邻接矩阵的特点：(www.daowen.com)

① 对角线上的元素均为0，同时邻接矩阵也是对称矩阵。

② 每行或每列的数据之和为对应顶点的边的数量。

③ 一般来说，邻接矩阵比关联矩阵小。

2.有向图的矩阵表示

（1）有向图的关联矩阵。

有向图关联矩阵的形式和无向图的关联矩阵（9.1）一样，唯一不同的是，有向图的关联矩阵中，元素aij按照如下确定：

例9.6　写出图9.23的关联矩阵。

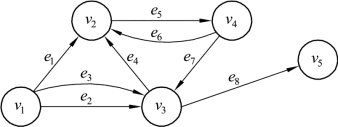
图9.23

解　图9.23的关联矩阵如下：

通过图9.23的关联矩阵，可以观察出有向图关联矩阵的特点：

① 第i行中1的个数是以顶点vi为起点的边的数量，-1的个数是以顶点vi为终点的边的数量。

② 第j列中的元素之和恒为0。

（2）有向图的邻接矩阵。

有向图邻接矩阵的形式和无向图的邻接矩阵（9.2）一样，唯一不同的是，有向图的邻接矩阵中，aij的值是以顶点vi为起点，以顶点vj为终点的边的数量。

例9.7　写出图9.23的邻接矩阵。

解　图9.23的邻接矩阵如下：

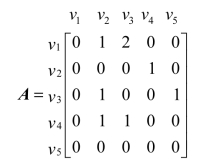
通过图9.23的邻接矩阵，可以观察出有向图邻接矩阵的特点：

① 对角线上的元素均为0。

② 第i行中的元素之和是以顶点vi为起点的有向边的数量。

③ 第j列中的元素之和是以顶点vj为终点的有向边的数量。

④ 同样，邻接矩阵比关联矩阵小。