图既然分为无向图和有向图，因此有必要分别介绍无向图和有向图的有关术语。需要注意的是，针对无向图和有向图，尽管有一些术语的名称和表述相同，但要注意本质上的差别。

1.无向图相关术语

平行边：无向图G中有相同端点的边称为平行边。如图9.6中，顶点v2和v4之间的两条边即为平行边。

简单图：如果无向图G中无平行边，则图G称为简单图。如图9.3、图9.4为简单图。

完备图：在无向图G中，若任意两个端点之间有且仅有一条边，则图G称为完备图。如图9.8为完备图。

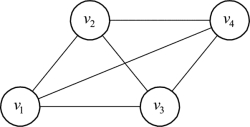
图9.8

链：无向图G中，两个端点之间的连接路径称为链。如图9.6中，v1和v5之间的连接路径v1v2v4v3v5即为链。一条链的起始端点和终止端点不为同一个端点的链称为开链，否则称为闭链，如图9.6中，链v1v2v4v3为开链，链v1v2v4v3v1为闭链。

初等链：在无向图G中，如果一条链中没有重复的顶点，则此链称为初等链。如图9.6中，链v1v3v4v2v3v5不是初等链，因为有重复的顶点v3，而链v1v2v4v3是初等链。

路：针对无向图G的一条链，若链中的每个点都不相同，则称这条链为连接链的起点和终点的路。如图9.6中链v1v2v4v3v5也称为路。

回路：在一个无向图的闭链中，如果除了起始端点和终止端点相同外，没有相同的顶点和相同的边，则此闭链也称为回路。如图9.6中，闭链v1v2v4v3v1是回路，而闭链v1v2v4v3v2v1就不是回路，因为有相同的顶点v2和相同的边(v1,v2)。

连通图：若无向图G中任意两点都能连通，则称无向图G为连通图，否则称为分割图。连通图中不存在任何孤立的顶点，即一个图中任意两点之间至少存在一条链，如图9.3、图9.4、图9.6、图9.8、图9.9都为连通图，若把图9.6的边(v3,v5)去掉，顶点v5就成了孤立的点，这样的图就不是连通图了。

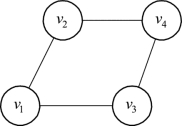
图9.9

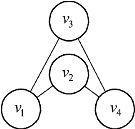
同构图：图反映了对象与对象之间的某种关系，所以顶点的标识、顶点的位置、顶点之间连线的长短曲直都是无关紧要的，重要的是顶点之间的连接情况，所以把结构一样的图互称为同构图。如图9.9和图9.10互为同构图。

(www.daowen.com)

图9.10

另外，假设Q为连通的无向图G的一条链，若图G中每一条边在链Q中恰好出现一次，则称链Q为欧拉链；若欧拉链是闭链，则该欧拉链称为欧拉环游；若连通的无向图G中含有一条欧拉环游，则图G称为欧拉图。

2.有向图相关术语

平行边：在有向图G中，起点和终点都相同的边称为平行边。如图9.11中，顶点v2和v4之间的两条边即为平行边。

简单图：若有向图G中无平行边，图G也称为简单图。如图9.7即为简单图。

完备图：若有向图G中，任意两个顶点之间恰好有两条非平行的有向边，则图G称为完备图。如图9.12即为完备图。

图9.12

基本图：去掉有向图G中所有有向边的方向，就能得到一个无向图G*，此无向图G*称为有向图G的基本图。如图9.6即为图9.7的基本图。

同构图：若有向图之间的顶点和边都能一一对应，则这些图互为同构图。

初等链：在有向图G的基本图G*中的初等链也称为有向图G的初等链。如图9.6中的初等链v1v2v4v3也是图9.7的初等链。

路：针对有向图G的一条链，若链中每个点都不相同，则称这条链为连接该链起点和终点的路。如图9.11中链v1v3v4v2称为路。

回路：起点和终点重合的路称为回路。如图9.11中路v1v3v4v2v1称为回路。

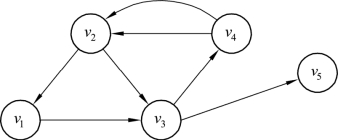
图9.11