1.资源配置问题

所谓资源配置问题，就是如何将有限的资源分配给若干个生产活动，并且使资源利用的收益最大。这是经济活动中比较常见的问题，而动态规划可以求解一些线性规划无法解决的资源配置问题。

设有数量为a的有限资源，现在分配给n个生产活动，已知把xi数量的资源分配给第i个生产活动的收益为fi(xi)，问题是如何分配资源才能使n个生产活动的总收益最大？

此问题即为一般的资源配置问题，可以描述为如下的规划问题：

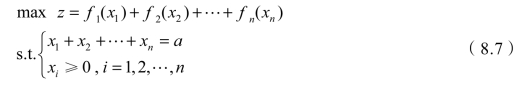
当fi(xi)是线性函数时，这就是线性规划问题；当fi(xi)是非线性函数时，这就是非线性规划问题。如果n较大时，求解相当繁琐，基于这类模型的特殊结构，可以把此问题看成是多阶段决策问题，这样就可以用动态规划的递推方程来求解。

由前面已经知道，决策变量xi表示分配给第i个生产活动的资源数量，设状态变量为si，表示分配第i个生产活动时剩余的资源数量，则有状态转移方程si+1=si－xi。同时可知允许决策集合为Xi(si)={xi|0≤xi≤si}。设最优后部指标的函数为fi(si)，表示把现有的数量为si的资源分配给第i个及以后的其余生产活动所得的最大总收益，至此可以写出此动态规划逆推的指标递推方程：

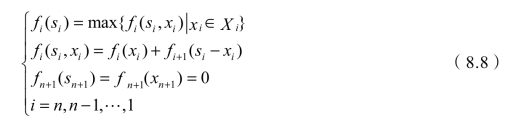
利用模型8.8即可逐段依次计算，最后求得的f1(a)即为此资源分配的最大总收益。

下面以一个具体例题介绍资源配置问题的动态规划求解过程。

例8.3　某工厂有4台设备要分配到3条生产线上，用变量xi表示分配到第i条生产线上的设备数量，可知xi=0,1,2,3,4，其中i=1,2,3。已知设备分配到不同生产线的预期收入函数分别为

f1(x1)=6x1+4、f2(x2)=4x2+6、f3(x3)=3x3+5

另外，若没有设备分配到生产线上，则预期收入应该为0，即当x1=x2=x3=0时，有f1(x1)=f2(x2)=f3(x3)=0，问设备如何分配到各条生产线上，才会使工厂的总收入最大？

解　此问题的阶段与生产线相联系，可以分为3个阶段，即n=3。状态变量si表示可供分配给第i条生产线的设备数量；决策变量xi表示最终分配给第i条生产线的设备数量，则有状态转移方程si+1=si－xi，同时可知允许决策集合为Xi(si)={xi|0≤xi≤si}；设最优后部指标的函数为fi(si)，那么动态规划逆推的指标递推方程为

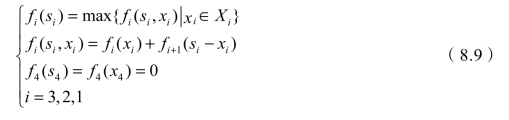
当k=3时，f3(x3)=3x3+5，分配设备的收入状态如表8.1所示：

表8.1　k=3时的收入状态

当k=2时，f2(x2)=4x2+6，s3=s2-x2，分配设备的收入状态如表8.2所示：

表8.2　k=2时的收入状态

当k=1时，f1(x1)=6x1+4，s2=s1-x1，分配设备的收入状态如表8.3所示：

表8.3　k=1时的收入状态

最终根据这些表格可以得出最优解为x1=2，x2=1，x3=1，工厂的最大总收入为34。

2.生产与库存问题（生产计划问题）

在实际问题中，经常会遇到安排生产或采购计划问题。要求在满足实际需求的情况下，使成本费用达到最低，因此，这就需要对生产计划或采购计划制定合理的策略，从而确定不同时期的生产量、采购量或库存量，以使生产成本和库存费用总和最小。这就是生产与库存问题的最优化目标。

下面以一个具体例题介绍生产与库存问题的动态规划求解过程。

例8.4　某生产厂家与一位客户签订生产合同，在4个月内出售一定数量的某种产品，该产品的每月生产成本会随着原材料的行情波动而变化。已知工厂每月最多生产80单位该产品，要求产量限于10的倍数。另外，对生产的多余产品可以储存，储存费用为每单位每月3元，其中该产品每个月的需求量及单位产品的生产成本如表8.4所示：

表8.4　需求量及单位产品生产成本

现在要求确定该产品每月的具体生产数量，使每月的合同需求量得到满足，同时又使生产成本和储存费用之和最小。

解　此问题的阶段与月份相联系，可以分为4个阶段，即n=4，用逆推法求解，第1阶段从4月份开始。状态变量is表示第i阶段开始时具有的产品数量；决策变量xi表示第i阶段产品的具体生产数量；ci表示第i阶段的单位生产成本；qi表示第i阶段的产品需求量；有状态转移方程si+1=si+xi-qi。设最优后部指标的函数为fi(si)，关于费用的直接指标函数表达式为fi(si,xi)=cixi+3si，则动态规划逆推的指标递推方程为

当k=4时，即对应于第1阶段，因为工厂每月最多生产80单位该产品，则前3个月最大产量为240单位，需求量为220单位，所以4月初最大储存量为20单位，产量又限于10的倍数，所以4月初可能的储存量为0、10、20单位；4月初的存储量加上4月的产量应该恰好等于4月份的需求量50单位，所以4月可能的产量为50、40、30单位，该阶段的决策如表8.5所示：

表8.5　k=4时的决策状态

当k=3时，对应第2阶段，与前一阶段同样的分析可知，3月初的最大储存量为50单位；因为工厂每月最多生产80单位，而3月需求量为110单位，所以3月初至少应该有储存量30单位，则3月可能的产量为80、70、60单位，该阶段的决策如表8.6所示。

表8.6　k=3时的决策状态

当k=2时，即对应于第3阶段，和前一个阶段同样的分析可知，2月初最大储存量为30单位；从前一个阶段可知，3月初至少应该有储存量30单位，那么有s2+x2-60≥30，即s2+x2≥90，这意味着本阶段初至少应该有存储量10单位，那么2月初可能的储存量应该为10、20、30单位，所以2月可能的产量为80、70、60单位。该阶段的决策如表8.7所示。

表8.7　k=2时的决策状态

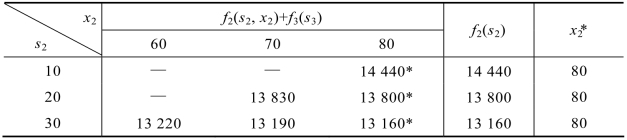
当k=1时，即对应于第4阶段，1月初储存量为0单位，需求量为50单位；从前一个阶段可知，2月初至少应该有10单位的存储量，那么1月可能的产量为60、70、80单位。该阶段的决策如表8.8所示。

表8.8　k=1时的决策状态

至此，4个月的最优生产计划制定完毕，如表8.9所示：

表8.9　最优生产计划

需要注意的是，在每个阶段计算fi(si,xi)时，无论si为何值，fi(si,xi)都是si的单调函数，即呈现出线性关系。

3.设备更新问题

在实际问题中，经常会遇到设备陈旧等原因造成的设备更新问题。一台设备在比较新的时候，故障较少，正常运转时间也较长，年收益也较高，但随着使用时间的增加，故障会越来越多，正常运转时间就减少，维修的费用会增加，年收益也减少。当达到一定程度时，就需要更新设备，其中涉及以旧换新的费用。因此在设备更新问题中，需要考虑计算期内设备更新几次，在哪一年更新，从而使计算期内总收益最大，即在n年内，每年年初都要对设备做出决定，是更换一台新的设备，还是继续使用旧设备，其目的就是在n年内总收益最大。

设备更新问题按计算期n年划分为n个决策阶段，对各种变量做如下定义：

状态变量sk表示第k阶段开始时，设备已经使用过的年数，其中各个阶段的每一状态都只能取两个值，即sk+1和1。当决策变量为sk+1时，表示继续使用原有设备，即下一阶段的状态为sk+1；当决策变量为1时，表示当年年初更新了设备，即下一阶段的状态为1。决策变量xk表示作出该决策后所达到的下一阶段的状态。rk(sk)表示在状态sk下，第k阶段的设备年收益。uk(sk)表示在状态sk下，第k阶段的设备年维修费用。ck(sk)表示在状态sk下，第k阶段的设备更新费用。状态转移方程为sk－1=xk。直接指标如下：

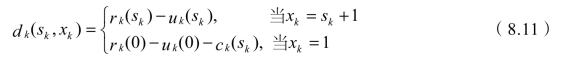
指标递推方程为

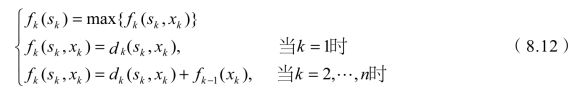
下面以一个具体例题介绍设备更新问题的动态规划求解过程。

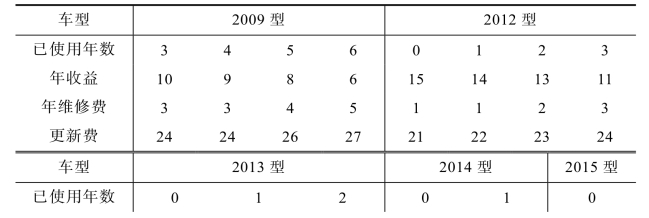
例8.5　某公交公司在2012年年初，考虑对一辆2009型公交车是否进行更新，这辆公交车是在2009年年初购进并投入运营，现已经使用3年。各种车型公交车的有关数据如表8.10所示，那么在2012年年初和以后3年的年初应该如何决策，才能使总的收益达到最大？

表8.10　各种型号公交车有关数据表

(www.daowen.com)

解　为便于用动态规划求解，将资料表8.10变换为表8.11。

表8.11　各种型号公交车有关数据表

第1阶段决策见表8.12：

表8.12　第1阶段决策表

计算举例如下：

f1(1,2)=d1(1,2)=r1(1)-u1(1)=16-1=15

f1(1,1)=d1(1,1)=r1(0)-u1(0)-c1(1)=18-1-22=－5

第2阶段决策见表8.13：

表8.13　第2阶段决策表

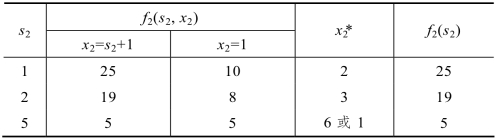
计算举例如下：

f2(1,2)=d2(1,2)+f1(2)=r2(1)-u2(1)+f1(2)=14-1+12=25

f2(1,1)=d2(1,1)+f1(1)=r2(0)-u2(0)-c2(1)+f1(1)=17-1-21+15=10

f2(2,3)=d2(2,3)+f1(3)=r2(2)-u2(2)+f1(3)=13-2+8=19

f2(2,1)=d2(2,1)+f1(1)=r2(0)-u2(0)-c2(2)+f1(1)=17-1-23+15=8

f2(5,6)=d2(5,6)+f1(6)=r2(5)-u2(5)+f1(6)=8-4+1=5

f2(5,1)=d2(5,1)+f1(1)=r2(0)-u2(0)-c2(5)+f1(1)=17-1-26+15=5

第3阶段决策见表8.14：

表8.14　第3阶段决策表

计算举例如下：

f3(1,2)=d3(1,2)+f2(2)=r3(1)-u3(1)+f2(2)=14-1+19=32

f3(1,1)=d3(1,1)+f2(1)=r3(0)-u3(0)-c3(1)+f2(1)=16-1-22+25=18

f3(4,5)=d3(4,5)+f2(5)=r3(4)-u3(4)+f2(5)=9－3+5=11

f3(4,1)=d3(4,1)+f2(1)=r3(0)-u3(0)-c3(4)+f2(1)=16-1-24+25=16

第4阶段决策见表8.15：

表8.15　第4阶段决策表

计算举例如下：

f4(3,4)=d4(3,4)+f3(4)=r4(3)-u4(3)+f3(4)=10-3+16=23

f4(3,1)=d4(3,1)+f3(1)=r4(0)-u4(0)-c4(3)+f3(1)=15-1-24+32=22

至此得出最优策略：2012年继续使用原来的公交车，2013年年初更新，2014年至2015年一直使用原来公交车，4年纯收益为23。

需要注意的是，在最优策略中，有可能在计划期内无需更新，也可能多次更新，这由问题的条件决定。另外，本题讨论的是一辆公交车，如果针对多辆公交车，同样按此方法，根据出厂日期是否相同分别计算。

4.背包问题（登山问题）

背包问题可以描述为一名登山者欲带一个背包登山，这名登山者最多可携带物品的重量为b千克。假设可供选择的物品有n种，已知第i种物品的重量为ai，携带第i种物品登山的作用价值为ci。此登山者在重量有限的背包里，携带哪些物品才使登山物品的总作用最大？

此类问题就是著名的背包问题，类似问题还有工厂下料问题、运输货物装载问题等。

设xi表示携带第i种物品的数量，则背包问题的模型如下：

从模型8.13可以看出，这是一个整数规划问题。如果每种物品只能携带一件，即xi只能取值为0或1，这个问题又是0-1规划问题。当然可以按照整数规划或0-1规划进行求解。

下面以一个具体例题介绍背包问题的动态规划求解过程。

例8.6　一架货运飞机，有效载重为24吨，可运载的物品重量及运费收入如表8.16所示，问题是该飞机运载哪几件物品才使总运费收入最多？

表8.16　物品重量及费用收入

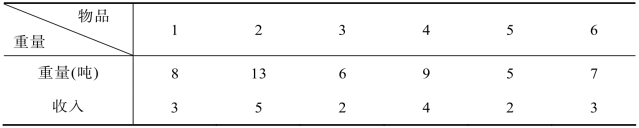
解　问题可以按照物品编号依次划分为6个阶段，用顺推法求解，先决定是否运送物品 1。对各种变量做如下定义：状态变量sk表示第k阶段飞机剩余的吨位；状态转移方程是sk-1＝sk-akxk，其中ak表示物品重量；决策变量xk表示是否运载k物品，若运送xk=1，否则xk=0。

第1阶段的可能状态是s1=0,1,…,24，因为物品1重量为8吨，所以将0,1,…,7吨并为一类，8,9,…,24吨并为一类，这样状态s1=0,1,…,7时，能够采取的决策是相同的，即x1=0，在这一阶段f1(s1,x1)=d1(s1,x1)，计算结果如表8.17所示：

表8.17　第1阶段时的决策表

计算举例如下：

第2阶段，对一切s2，有d2(s2,0)=0；对s2≥13，有d2(s2,1)=5，此阶段状态转移方程是s1=s2-13x2。借鉴上一状态，针对本阶段可能的状态，把具有相同计算结果的状态也合并，即将0～24吨分为0～7、8～12、13～20、21～24四个区间，计算结果如表8.18所示：

表8.18　第2阶段时的决策表

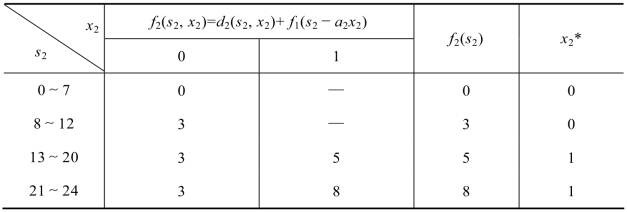
计算举例如下：

当s2=8～12时，f2(s2,0)=d2(s2,0)+f1(s2-0)=0+3=3；

当s2=21～24时，f2(s2,1)=d2(s2,1)+f1(s2-13)=5+3=8。

第3阶段，把具有相同计算结果的状态也合并，即状态区间为0～5、6～7、8～12、13～13、14～18、19～20、21～24，计算结果如表8.19所示：

表8.19　第3阶段时的决策表

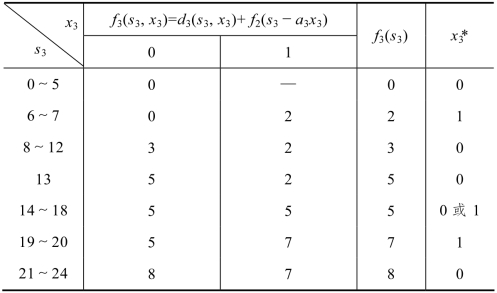
同理可以计算第4、5、6阶段（过程省略）。

特别提示

在现实问题中，动态规划的问题很多，比如还有推销员问题、排序问题、复合系统可靠性问题等等。