构建好动态规划模型以后，就需要对此模型进行求解。根据状态转移方程和指标递推方程，如果按照与实际过程相反的方向求解，即从实际决策的最后阶段向最初阶段进行递推来寻求最优策略，这种方法称为逆推法或逆序法；如果按照与实际过程相同的方向求解，即从实际决策的最初阶段向最后阶段进行递推来寻求最优策略，这种方法称为顺推法或顺序法。

一般来说，当初始状态给定时，用顺推法相对比较方便；当终止状态给定时，用逆推法相对比较方便。

1.逆推法

运用逆推法求解时，需根据实际决策从最后阶段n开始，即边界条件从k=n开始，由后向前进行逆推，逐步求得各个阶段的最优决策和相应的最优值，最后求得最优后部指标即最初阶段的最优指标f1(s1)，从而得到整个问题的最优解。这种由后向前推算最优解的方法称为逆推法，相应的基本方程称为逆推法基本方程。

动态规划逆推法的基本方程为

或写成

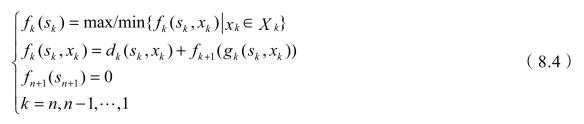
逆推法的求解过程就是根据边界条件fn+1(sn+1)=0，从k=n开始，由后向前进行逆推，根据基本方程求出各个阶段的fk(sk)，最后求得的f1(s1)就是整个动态规划问题的最优解。

2.顺推法

运用顺推法求解时，需根据实际决策从最初阶段开始，即边界条件从k=1开始，由前向后进行顺推，逐步求得各个阶段的最优决策和相应的最优值，最后求得最优后部指标即最后阶段的最优指标fn(sn)，从而得到整个问题的最优解。这种由前向后推算最优解的方法称为顺推法，相应的基本方程称为顺推法基本方程。

动态规划顺推法的基本方程为

或写成

(www.daowen.com)

顺推法的求解过程就是根据边界条件f0(s0)=0，从k=1开始，由前向后进行顺推，根据基本方程求出各个阶段的fk(sk)，最后求得的fn(sn)就是整个动态规划问题的最优解。

为了对动态规划问题的求解有更具体的理解，在前面例8.1求解分析基础上，现在用逆推法对例8.1进行求解，即从终点E由后向前逐段向始点A方向寻找最短路线。

从图8.1可知，此问题分为5个状态和4个阶段，所以此问题可分为4个阶段进行决策，过程如下：

当k=4时，设边界条件f5(s5)=f5(E)=0，则通过以下指标递推方程作出决策：

当k=3时，则通过以下指标递推方程作出决策：

当k=2时，则通过以下指标递推方程作出决策：

当k=1时，则通过以下指标递推方程作出决策：

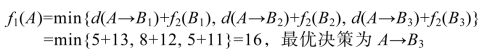
针对上述各阶段进行反向追踪可知，从A到E的最优决策为A→B3→C2→D1→E，即为A到E的最短路线。

当然，针对例8.1也可以用顺推法进行求解。