为了对动态规划有一个初步的认识，下面先给出两个例子。

1.最短路问题

例8.1　图8.1为网络图，图中连线上的数字表示两点间的距离。

针对图8.1，需要在A点和E点之间最短的线路上铺设一条管道。由图可知，铺设线路时要经过三个点，第一个点可以是B1、B2、B3中的某一个点，第二个点可以是C1、C2、C3中的一个点，第三个点可以是D1、D2中的一个点，要求把各点之间能铺设管道的连线在图中标识出来。

求解的一般思路是用穷举法求最短路，即为了求出最优决策，可以用穷举法穷举出A到E的所有路线，并计算每条路线的长度，然后找出最短路。

基于图8.1，针对节点分为5个状态，针对过程分为4个阶段，所以此问题可以分为四个阶段进行决策。在阶段1，从起点A出发，终点可以选择B1、B2或B3；在阶段2，若在第一阶段选择B1，终点可以选择C1、C2或C3；若在第一阶段选择B2，终点也可以选择C1、C2或C3；若在第一阶段选择B3，终点同样可以选择C1、C2或C3。针对其余阶段，可以依此继续下去，直到达到E。本例题共18条不同的路线，通过比较它们的长度，最短路线为A→B3→C2→D1→E，其长度为16。

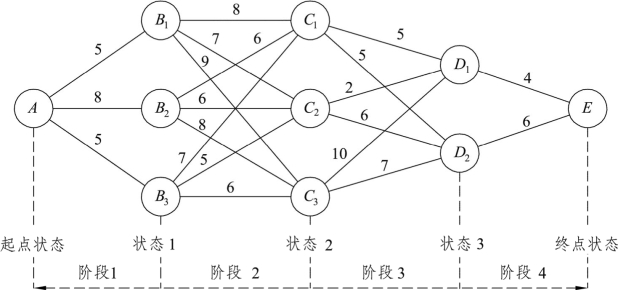
图8.1

当可供选择的状态比较多，而决策阶段也比较多时，再采用穷举法就会相当复杂，甚至无法实现决策的目的。

下面针对此例题做一下分析。

如果最短路线通过M和N两点，则这条路线从M点（或N点）到达终点的部分，对于M点（或N点）至终点的所有路线而言，必定也是最短路线，简言之就是M点（或N点）的后部路线必定也是最短路线。所以从上例中可以看出，路线C2→D1→E就是C2至E中所有路线的最短路线。这个特性非常容易理解，假设如果从M点至终点还有一条更短的路线存在，则把它和原来最短路线从起点开始的那一部分连接起来，就会形成一条比原来的最短路线更短的路线，这样就出现两条最短路线，显然与事实不符，这就是最短路线问题求解的一个特性，即最短路线中的任意节点的后部路线也是最短路线。

基于此特性，对此例题的求解分析如下：

第一步：先从最后阶段即阶段4考虑，这一阶段分别要对D1和D2找出最短路线。由于D1至E只有一条路线，因而D1的最短后部路线即为D1→E，其长度为4。由前面最短路线问题的特性可知，如果A至E的最短路线经过D1，那么从D1至终点E的最短路线必为D1→E。同理，D2的最短后部路线为D2→E。为了记录整个问题的决策过程，在图8.1基础上，把D1至E最短路线的长度4填到多边形框内，标在节点D1的旁边。同样，把D2至E最短路线的长度6填到多边形框内，标在节点D2的旁边，如图8.2所示。

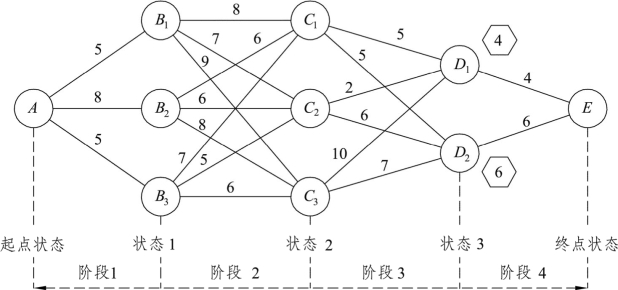
图8.2

第二步：现在从倒数第二阶段即阶段3考虑，这个阶段要找出C1、C2、C3的最短后部路线。

C1的后部路线有C1→D1和C1→D2。后部路线C1→D1→E的长度为C1→D1的长度5加上D1多边形框内的数字4，即后部路线C1→D1→E的长度为9。同理，后部路线C1→D2→E的长度为C1→D2的长度5加上D2多边形框内的数字6，即后部路线C1→D2→E的长度为11。比较这两个后部路线的长度，可以确定C1的最短后部路线是C1→D1→E，则将C1的最短后部路线的长度9填到多边形框内，标在节点C1的旁边。

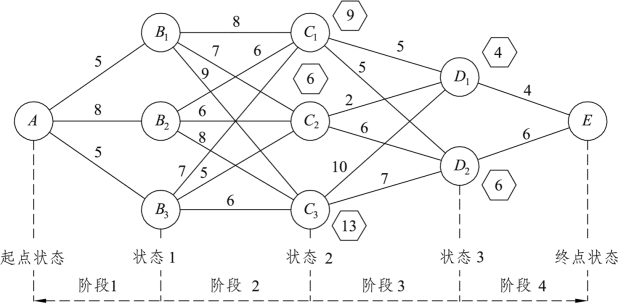
C2的后部路线有C2→D1和C2→D2。后部路线C2→D1→E的长度为C2→D1的长度2加上D1多边形框内的数字4，即后部路线C2→D1→E的长度为6。同理，后部路线C2→D2→E的长度为C2→D2的长度6加上D2多边形框内的数字6，即后部路线C2→D2→E的长度为12。比较这两个后部路线的长度，可以确定C2的最短后部路线是C2→D1→E，将C2的最短后部路线长度6填到多边形框内，标在节点C2的旁边。用以上同样的方法可以找出C3的最短后部路线为C3→D2→E，其长度为13，也标在节点C3的旁边。此步骤的标注如图8.3所示。

(www.daowen.com)

图8.3

第三步：现在从倒数第三阶段即阶段2考虑，这个阶段要找出B1、B2、B3的最短后部路线。

用前面同样的方法可以找出B1的最短后部路线为B1→C2→D1→E，其长度为13；B2的最短后部路线为B2→C2→D1→E，其长度为12；B3的最短后部路线为B3→C2→D1→E，其长度为11，此步骤的标注如图8.4所示。

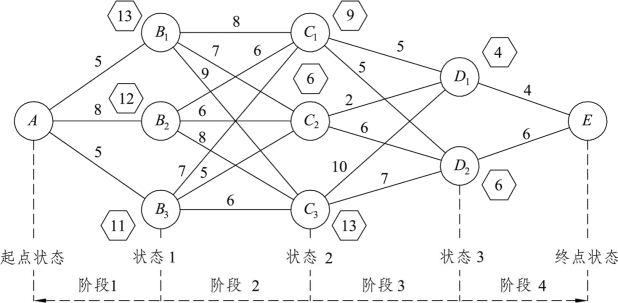
图8.4

第四步：现在从倒数第四阶段即阶段1考虑，这个阶段要找出A的最短后部路线，A的后部路线有A→B1、A→B2和A→B3。也同样用上述方法求出后部路线A→B1的长度为18，后部路线A→B2的长度为20，后部路线A→B3的长度为16。比较这三个后部路线的长度，可以确定A的最短后部路线是A→B3→C2→D1→E，则将A的最短后部路线的长度16填到多边形框内，标在节点A的旁边。

本题解题过程可以说至此已结束，我们也得到了从A开始到E的最短路线。把从A到E的最短路径用粗实线连接起来，此步骤的标注如图8.5所示。

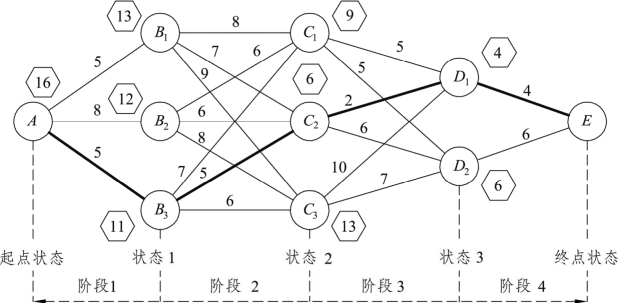
图8.5

以上例子就是用动态规划求解最短路线的典型方法。可以看出，用动态规划求解最短路线问题的特点就是把一个大的决策问题分解成若干个相互关联的小的决策问题，然后通过逐步求解小的决策问题，而且每个小问题的决策方法基本相同。

以上例子的求解也为理解动态规划的特点、动态规划的建模思路、动态规划的求解原理等奠定了认知的基础。

2.资源分配问题

例8.2　设某种资源的数量为m，将它投入到A、B两种生产中。若把n数量的资源投入生产A，把剩下的资源m-n投入生产B，则收入函数为φ(n)+γ(m-n)。若生产后可以进行回收再生产，设A、B回收率分别为a和b，其取值范围分别为0≤a≤1、0≤b≤1，则在第一阶段生产后回收的总资源为m1＝an+b(m-n)，再将m1投入生产A、B。若以n1和m1-n1再分别投入生产A、B，则又可得到收入φ(n1)+γ(m1-n1)，因此两阶段的总收入为φ(n)+γ(m-n)+φ(n1)+γ(m1-n1)。

如果上面的过程进行了k个阶段，而且希望选择n,n1,…,nk-1，使k个阶段的总收入最大，问题就变为

满足条件

其中0≤n≤m、0≤n1≤m1、…、0≤nk-1≤mk-1。可以将该例题分成k个阶段，用每个阶段的资源数表示该阶段的状态，即分配给A的资源数ni(i=1,2,…,k-1)表示决策这一过程，那么就可以通过mk＝ank-1+b(mk-1-nk -1)表示递推关系即状态转移，k个阶段的总收入z表示效益。