尽管0-1规划的求解方法很多，但最常想到的却是穷举法，也称为全枚举法。全枚举法就是检查每个变量等于0或1的每一种组合，而满足所有约束条件并使目标函数值最优的组合就是0-1规划的最优解。在0-1规划中，变量有n个，变量的组合有2n个，当变量的个数比较少、约束条件比较简单时，使用穷举法求解0-1规划问题比较简单明了，但如果变量个数n较大时，如n>10，这种全枚举的组合检查几乎是不可能完成的，因此需要设计一种过滤的方法，以使检查范围缩小，即只检查部分组合，这样的方法称为隐枚举法。

其实在7.1.3节介绍的分枝定界法也是一种隐枚举法，这里介绍的隐枚举法就是借助分枝定界法的思路。也可以说，隐枚举法是将过滤枚举和分枝定界方法结合在一起来求解0-1规划问题。为了介绍隐枚举法，设以下模型是0-1规划的标准型：

其中cj≥0，bi可以是正数、负数或0，所有约束条件方程式必须是“≤”的形式。

如果构建的0-1规划模型不是标准形式，可以通过以下方法转换为标准形式：

（1）如果目标函数是max型，将目标函数乘以1-后变为min型。

（2）如果某一个变量xj在目标函数中的系数cj<0，处理方法则是用1-xj把xj替换，如

可令x2＝1-x2，目标函数变为

即有

同样，约束条件方程也要作相应的处理。若求出的最优解中xj=0，则原有的xj=1；反之，若xj=1，则原有的xj=0。

（3）如果约束条件方程是“≥”形式，可将不等式两端乘以-1，变为“≤”形式。

（4）如果约束条件方程是“=”形式，可先将它变为“≤”和“≥”形式的两个约束条件方程，然后对“≥”形式的方程两端乘以-1，使其变为“≤”形式。

隐枚举法求解0-1规划问题的思路与分枝定界法有相同之处，但隐枚举法主要是利用变量只能取0或1两个值的特点进行分枝。首先令全部变量取0值，然后检验这个组合解是否可行。若可行，则这个组合解即为最优解，目标函数值z=0，因为目标函数的系数都是正数，因而不会出现目标函数值小于0的可行解；若不可行，则令一个变量取值分别为0和1，此变量称为固定变量，然后将问题分成两个子域，其余未被指定取值的变量称为自由变量，如此继续进行，不断扩大固定变量的数量，直到寻找到最优解。

隐枚举法的具体步骤如下：

第一步：令全部xj都是自由变量，并且取值都为0，检验这个取值都为0的组合解是否可行。若可行，说明已经取得最优解，停止计算，否则转到第二步。

第二步：将某一个自由变量设为固定变量，令其取值分别为1和0，把问题分成两个子域。然后令其中一个子域中的自由变量都取0值，加上固定变量的取值，可组成此子域的一个解。再对另外一个子域做同样处理。

第三步：分别对两个子域的解依次进行如下三个方面的检验：

（1）定界。

计算此解的目标函数值。如果此目标函数值大于前面已求出的可行解的最小目标函数值，说明此解不如前面已求出的可行解优，则停止分枝，退出检验。

（2）可行性检验。

检验解是否可行。如果可行，就得到一个可行解，并计算出对应的目标函数值，退出检验。(www.daowen.com)

（3）子域可行性检验。

将子域中固定变量的值代入第一个不等式约束条件方程，针对该不等式左端的自由变量，当其系数为负值时，该自由变量的取值设为1；当其系数为正值时，该自由变量取值设为0。这就是第一个不等式约束条件方程左端所能取的最小值。若此最小值大于右端值，则称此子域为不可行子域，不再往下分枝，并退出检验；若此最小值小于右端值，则按照以上方法依次检验下一个不等式约束条件方程，直至所有的不等式约束条件方程都通过检验。

第四步：如果存在需要分枝的子域，就任选一个子域，转到第二步；如果没有，计算停止，使目标函数值最小的可行解就是最优解。

由于第三步有停止分枝的情况，且对子域中自由变量取0或1的一切可能组合没有一一列举，即都被隐含处理，与全枚举法比较，计算量大为减少，这就是隐枚举法的来历。

现举例说明隐枚举法的计算步骤。

例7.5　解如下0-1规划问题。

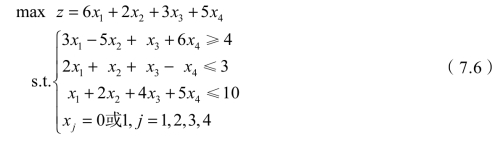
解　此模型不是标准形式，需要通过前面的方法进行变换。先将目标函数乘以-1，将其变为min型。但这样处理后目标函数的系数均变成了负数，这就需要把模型中所有的xj用1-xj替换，再把第一个约束条件方程变为“≤”形式。模型7.6的标准形式如下：

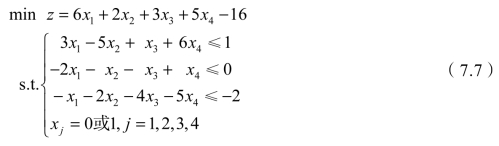
模型7.7的二叉树枚举图如图7.6所示：

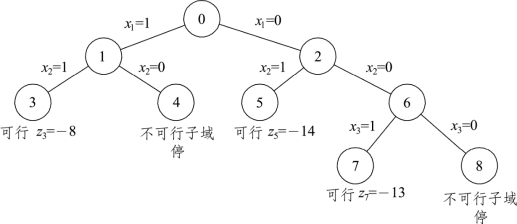
图7.6

令初始最优解的目标函数值z=+∞，下面对树中的几个子域加以说明：

先将全部变量都作为自由变量，则有组合(0,0,0,0），这个取值都为0的组合解不满足第三个约束条件方程，不可行；把变量x1设为固定变量，把问题分成两个子域，即得到子域1和2。

对子域 1 的解(1,0,0,0)进行检验计算，z1=-10<z；进行解的可行性检验，此解不可行；进行子域的可行性检验，能通过三个不等式约束条件方程，需要对子域1进行分枝。再将变量x2设为固定变量，分别令x2=1和x2=0，构成子域3和子域4。

子域3的解(1,1,0,0)可行，z3=-8<z，停止分枝，此时设z=z3=-8。子域4的解为(1,0,0,0)，z4=-10<z；进行子域的可行性检验，将x1=1和x2=0代入第一个约束条件方程，并令x3=x4=0，求出左端的可能最小值为3，大于右端值1，可知子域4是不可行子域，不再进行分枝。

对子域2的解(0,0,0,0)进行检验计算，z2=-16<z；进行解的可行性检验，此解不可行；进行子域的可行性检验，能通过三个不等式约束条件方程，需要对子域2进行分枝。将变量x2设为固定变量，分别令x2=1和x2=0，构成子域5和子域6。

子域5的解(0,1,0,0)可行，z5=-14<z，停止分枝，此时设z=z5=-14。对子域6的解(0,0,0,0)进行检验计算，z6=-16<z；进行解的可行性检验，此解不可行；进行子域的可行性检验，能通过三个不等式约束条件方程。需要对子域6进行分枝，分别令x3=1和x3=0，构成子域7和子域8。

子域7的解(0,0,1,0)可行，z7=-13，停止分枝，但z7>z，保持z=-14不变。而子域8的解为(0,0,0,0)，z8=-16<z；进行解的可行性检验，此解不可行；进行子域的可行性检验，将x1=0、x2=0、x3=0代入三个约束条件方程，并令x4=0，求出左端的可能最小值为0，大于右端值-2，可知子域8是不可行子域，不再进行分枝。

所有子域都停止了分枝，说明已经得到最优解，所以针对模型7.7的最优解就是子域5的解(0,1,0,0)，z=-14。

因为在前面把原有模型7.6转换为标准模型7.7时，用1-xj替换了xj，所以在模型7.7中等于0的变量，在模型7.6中就应该等于1，反之，在模型7.7中等于1的变量，在模型7.6中就应该等于0，因此针对模型7.6的最优解就是(1,0,1,1)，z=14。

特别提示

在解题时，为了使计算过程尽可能少一些，也为了使计算速度尽可能快一些，在隐枚举法的第二步中，争取把最小的目标函数系数对应的自由变量设定为固定变量，因为目标函数系数最小的变量对目标函数的影响也最大。