库恩（W.W.Kuhn）于1955年引用了匈牙利数学家康尼格（D.Konig）的一个关于矩阵中0元素的定理，从而提出了指派问题的解法，这个解法称为匈牙利法。虽然后来这种方法不断改进，但这个名称一直沿用至今。

在学习匈牙利法之前，先给出相关分析及有关的定理。

相关分析　对指派问题的求解就是基于完成任务的时间表，按照总时间花费最小的目标进行任务分配。而指派问题目标函数的系数恰恰是完成任务的时间表的值，所以可以把完成任务的时间表的值构造成一个矩阵，把这个矩阵称为系数矩阵。

现在基于表6.2（完成任务时间表中的值），构造如下的系数矩阵C：

而对指派问题的求解，可以转换为针对系数矩阵C找出n个取值为1的决策变量。

定理6.1　如果对系数矩阵C中任意行或列的各元素cij分别加上或减去一个数，会得到一个新矩阵B。设新矩阵B中的元素为bij，则基于新矩阵B中的系数bij为指派问题的最优解，且和原问题的最优解相同。

证明　指派问题的目标函数为

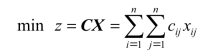
设系数矩阵C为

把系数矩阵C中第k行的每个元素都加上一个常数d，则系数矩阵C变为

那么基于新矩阵B的指派问题的目标函数就变为

又由约束条件方程可知，所以

z′=z+d

这就是说，新目标函数z′与原来的目标函数z仅相差一个常数d，所以基于新矩阵B的系数bij为指派问题的最优解，且和原问题的最优解相同。

同样，系数矩阵C中任一列的每个元素都减去一个常数d以后，也会与前面的结论一样。

根据上面的定理，如果把指派问题系数矩阵的一行或一列的各元素分别减去该行或该列的最小元素，就可以使系数矩阵的每一行和每一列中至少出现一个0元素，把这个变化后的矩阵称为等效矩阵。

基于以上的相关分析和定理，为了更好地掌握匈牙利法，下面结合具体的示例计算，给出匈牙利法的主要步骤：

第一步：将指派问题给出的时间表构造成系数矩阵C。

针对例6.1的表6.1，构造如下系数矩阵C：

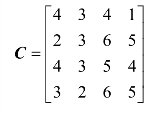
第二步：针对系数矩阵建立等效矩阵B，使各行各列都出现0元素。方法如下：

（1）把系数矩阵的每行元素减去该行的最小元素。

（2）再把所得矩阵的每列元素减去该列的最小元素。

若某行或某列已有0元素，就不必再处理。

针对上一步的系数矩阵C，可构造等效矩阵B，过程如下：

第三步：针对等效矩阵B进行初始分配。经过变换后的等效矩阵B，每行每列都已有了0元素，此时需要找出n个位于不同行不同列的独立的0元素，即试指派以寻求最优解。若能找出，可将这些独立的0元素所对应的变量取值为1，其余变量的取值为0，进而得到指派问题的最优解。当n较小时，用观察法、试探法可以找出n个独立的0元素，但当n 较大时，就必须按照一定的方法来寻找n个独立的0元素。方法如下：

（1）行检验。从只有一个0元素的行开始，给这个0元素加上“（）”，标记为（0），这表示该行所代表的人有了一个任务的指派；然后划去（0）所在列的其他0元素，这表示该列所对应的任务已指派给当前行所对应的人，故不能再指派给其他人。如果遇到有两个以上0元素的行，暂不处理。

（2）列检验。原理和行检验一样，给只有一个0元素的列中的0元素加上“（）”，标记为（0），然后划去（0）所在行的其他0元素。如果遇到有两个以上0元素的列，暂不处理。(www.daowen.com)

（3）再对两个以上0元素的行和列进行标记，即任意取一个0元素并加上“（）”，然后再按照（1）和（2）的思路进行处理。

（4）如果（0）的个数已经达到n个，则说明得到了最优解，计算停止，否则转第四步。针对上一步的等效矩阵B，进行行检验和列检验，如下所示：

行列检验后，（0）的个数已经达到了4个，说明得到了最优解。把这些独立的（0）元素所对应的变量取值为1，其余的变量取值为0，可得到最优解的矩阵：

最优的目标函数值z=c14+c21+c33+c42=1+2+5+2=10。

上面的例题经过以上三个步骤求出了最优解，但有的系数矩阵经过以上三个步骤后仍然不能求出最优解，如系数矩阵C及其等效矩阵B：

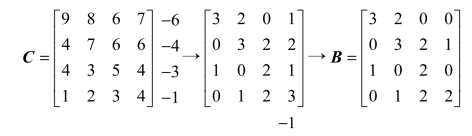
对上面的等效矩阵进行行列检验后，结果如下：

在行列检验的初始分配后，位于不同行不同列的0元素只有三个，即独立的（0）元素只有三个，而此指派问题n=4，所以未能求出最优解，需要转入第四步进行求解。

第四步：作最少的直线以覆盖所有的0元素，并确定在等效矩阵B中能找到最多的独立元素。这可按下列步骤进行：

（1）找出所有没有（0）的行，然后在矩阵右侧对应的行位置标记△。

（2）找出已经标记△的行中所有含0元素所对应的列，然后在该列矩阵的下边标记△。

（3）找出标记△的列中含（0）的行，然后在该行矩阵的右侧再标记△。

（4）重复（2）、（3）步，直到找不出可以打△号的行或列为止。

（5）对没有打△的行画一横线，对打△的列画一纵线，可得到覆盖所有0元素的最少的直线数。

针对上一步的矩阵，作最少的直线覆盖所有的0元素，结果如下：

第五步：对上面矩阵进行变换的目的是增加0元素，为此在没有被直线覆盖的元素中再找出最小元素，然后按下列步骤进行：

（1）在打△的行中，将非0的各元素减去这一最小元素。

（2）在打△的列中，将非0的各元素加上这个最小元素。

以上处理的目的就是保证原来的0元素不变，进而又得到另外一个新矩阵，基于它的最优解与原问题仍然相同。

针对上一步的矩阵，没有被直线覆盖的元素中最小元素为1，处理结果如下所示：

第六步：返回第三步，继续求解，直到找到位于不同行不同列的n个（0）元素后，即得到了最优解，计算停止。

针对上一步的矩阵，继续求解，处理结果如下所示：

矩阵中（0）的个数已经达到了4个，说明得到了最优解，把这些独立的（0）元素所对应的变量取值为1，其余变量的取值为0，则最优解的矩阵如下：

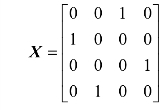
最优的目标函数值z=c13+c21+c34+c42=6+4+4+2=16。