1.指派问题的线性规划模型描述

为了更好地了解指派问题及其模型结构，先给出以下的引例。

例6.1　有装载货物的4辆待卸车，需要分派给4个装卸班组，每个班组只能卸1辆待卸车，同时每个待卸车只能由1个班组卸。由于技术专长不同，各个班组卸不同车辆所需要的时间如表6.1所示。那么应该如何分配卸车任务，才使卸车所花费的总时间最小？

表6.1　卸车时间表（小时）

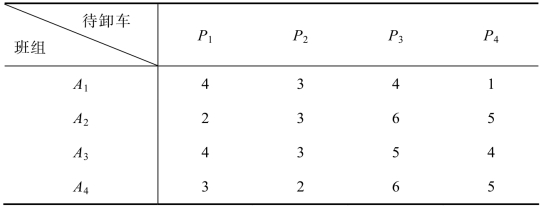
解　设决策变量xij表示第i班组卸第j辆车，当xij=1时，表示第i个班组卸第j辆车；当xij=0时，表示第i个班组不卸第j辆车。由卸车所需要的时间列出目标函数，再根据4个装卸班组和4辆待卸车分别列出相对应的约束条件方程，那么卸车所花费总时间最小的线性规划模型为

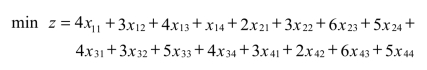
基于上例可以建立此类问题的通用描述：

有n项任务需要分派给n个工作人员去完成，每个工作人员只能完成1项任务，同时每项任务只能由1个工作人员完成。每个工作人员完成不同任务所需要的时间如表6.2所示，应该如何分配才使完成任务所花费的总时间最小？

表6.2　时间表

解　设决策变量xij表示第i个工作人员完成第j个任务，则xij的取值为

基于问题可知：花费的总时间等于每个工作人员完成每项任务的时间之和，即有

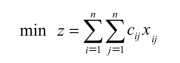
每个工作人员只能完成1项任务，即有；(www.daowen.com)

每项任务由1个工作人员完成，即有。

这样就可以把上面问题的线性规划模型归纳如下：

式（6.2）就是指派问题线性规划模型的通用形式。除了经常遇到n个人完成n个任务之外，在其他的活动中也会遇到诸如此类的问题。把具有模型（6.2）的形式和特点的线性规划问题称为指派问题。

一般地，指派问题的目标函数是min型，工作人员数和任务数是相等的，把符合这类特点的指派问题称为标准指派问题，否则称为非标准指派问题。至于出现目标函数是max型或工作人员数和任务数不相等的非标准指派问题将在第6.3节中讲到。

2.指派问题线性规划模型的特点

通过观察指派问题的线性规划模型，发现其具有如下特点：

（1）所有的约束条件方程（不包括决策变量的取值约束）都是等于1的等式。

（2）决策变量的取值只能是0或1。

（3）它包含n2个决策变量。

（4）模型有2n个约束条件方程。

（5）前n个方程说明i个人完成j个任务。

（6）后n个方程说明j个任务由i个人完成。

（7）从模型的结构来看，指派问题是运输问题的特例；从决策变量的取值来看，它是线性规划中的0-1规划问题。

指派问题既然是运输问题的特殊形式，那么就可以用运输问题的表上作业法求解，但是用此方法会产生严重的退化问题。指派问题也是线性规划中的0-1规划问题，可以用第7章讲到的整数规划或0-1规划的解法求解，但这样求解如同用单纯形法求解运输问题一样。因此，基于指派问题的特点，下面介绍另外一种可行、简便的方法，即下一节将要介绍的指派问题的求解方法——匈牙利法。