在实际问题中，往往会遇到产地的产量或销售地的销量是不确知的情况，即产量或销量在一定的范围内，如a1≤ai≤a2或b1≤bj≤b2。这类运输问题就是非确定型的运输问题，同时这种非确定型运输问题的产销也是不平衡的。

针对这种非确定型的运输问题，处理思路就是首先设法将其转化为确定型运输问题，然后再转换为产销平衡的运输问题，最后用表上作业法求解即可。这种情况下的运输问题，就要把一个产地拆成两个“产地”，其中一个产量为a1，另一个产量为a2－a1，或者是把一个销售地拆成两个“销售地”，其中一个销量为b1，另一个销量为b2-b1，单位运费参照前面所讲的内容设置，这样就把这类非确定型的运输问题化为确定型的运输问题。

下面以一个例题具体说明这类非确定型运输问题的处理方法。

例5.5　某公司把物资从三个产地A1、A2、A3运往四个销售地B1、B2、B3、B4，可知A1发出物资至少为5吨且最多为9吨，A2发出物资只能有4吨，A3发出物资至少为8吨；B1、B2、B3、B4的销量分别为3吨、6吨、5吨、6吨。从各产地到销售地的单位产品运价如表5.34所示，设计该公司调运尽可能多的产品但总运费最少的方案。

表5.34　单位产品运价表

解　把产量、销量和单位产品运价整合到一张表格中，如表5.35所示：

表5.35

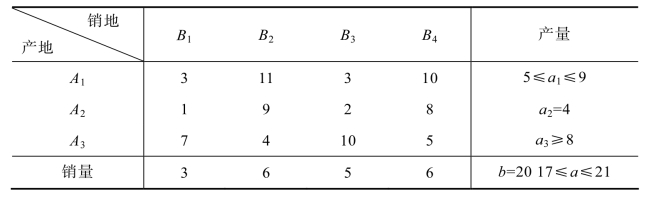
可知产地发出物资之和至少为5＋4＋8＝17吨，销售地的总销量为20吨。产地A3最多发出物资20－(5＋4)＝11吨。这样发出物资总量最多可达9＋4＋11＝24吨，大于销售地的总销量20吨，属于不平衡运输问题，这就需要增加一个虚拟的销售地B5，销量为24-20＝4吨。(www.daowen.com)

对产地A1、A3发出物资的情况分析如下：

A1必须发出物资5吨，但不能发往虚拟的销售地B5，所以运费c15要设为充分大的数M；A1最多发出物资9吨，那么剩余的4吨物资发出不发出均可，所以设相对应的运费为0。这样就需要把原来的产地A1拆成两个产地，一个仍然用A1表示，产量为5吨，另外一个用A1*表示，产量为4吨。

同理，A3必须发出物资8吨，但不能发往虚拟的销售地B5，所以运费c35就要设为充分大的数M；因为A3最多发出物资11吨，那么剩余的11-8＝3吨物资发出不发出均可，所以设相对应的运费为0。这样就把原来的产地A3拆成两个产地，一个仍然用A3表示，产量为8吨，另外一个用A3*表示，产量为3吨。

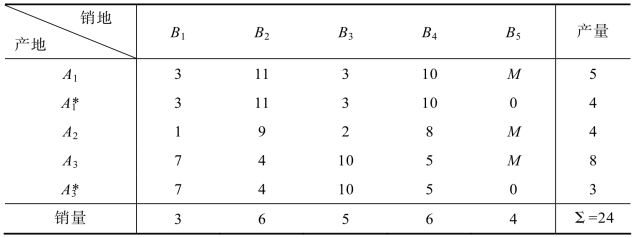
通过上面的分析，就把这个非确定型的运输问题转化成了确定型运输问题，同时也达到了产销平衡状态，现在可以生成平衡表5.36：

针对表5.36，用表上作业法即可求出调运物资的最少运费方案（求解过程省略）。

表5.36　平衡表

特别提示

对于销售量不确定或产量和销售量都不确定的运输问题的处理，可参照上例运输问题的处理方法即可。