前面讨论的运输问题及表上作业法的求解，都是以产销平衡为前提条件，但在实际问题中，往往会遇到产销不平衡的运输问题，即产量之和与销量之和不相等的运输问题。运输问题中出现产量之和不等于销量之和的情况有两种：

（1）产量之和大于销量之和，即所谓的“供过于求”现象。

（2）产量之和小于销量之和，即所谓的“供不应求”现象。

针对这两类产销不平衡的运输问题，处理思路就是设法将其转化为产销平衡的运输问题，然后再用表上作业法进行求解。通过下面两个处理过程，可以把产销不平衡的运输问题转换为产销平衡的运输问题，然后用表上作业法求解即可。

1.总产量大于总销量，即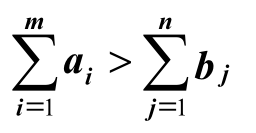

当总产量大于总销量时，产销平衡的转换方法就是虚拟一个销售地Bn+1，并令其销量为产量之和减去销量之和，即

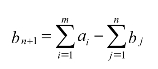
在实际问题中，可以把虚拟的销售地Bn+1看作存储点，如果不考虑存储费用，各个产地到虚拟销售地Bn+1的单位运费为零，否则就等于实际的单位存储费，这样就将总产量大于总销量的不平衡问题转换为产销平衡的运输问题，然后用表上作业法求解即可。

例5.3　表5.29是把产量、销量及单位产品运价整合在一起的某运输问题的综合表：

表5.29

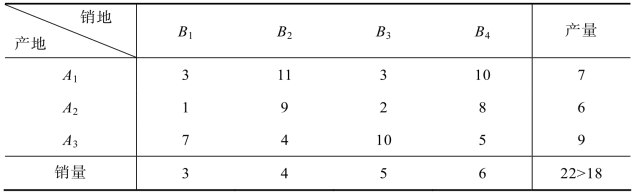
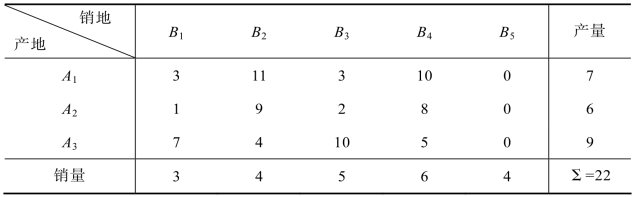
通过表5.29可以看出，产地的总产量为22，销售地的总销售量为18，产销不平衡，所以产销平衡的转换方法就是虚拟一个销售点B4+1，即增加一个销售点B5，并令其销量b4+1为产量之和减去销量之和，即b5＝22-18＝4。假设不考虑存储费用，则三个产地到虚拟销售点B5的单位运费为零，这样就可以构造出此运输问题的综合平衡表，如表5.30所示：

表5.30是运输问题的平衡表，用表上作业法求解即可。

表5.30

2.总产量小于总销量，即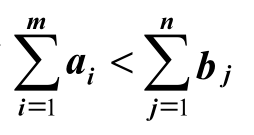

当总产量小于总销量时，产销平衡的转换方法就是虚拟一个产地Am+1，并令其产量为销量之和减去产量之和，即(www.daowen.com)

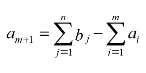
在实际问题中，可以把虚拟产地Am+1的产量am+1看作实际的缺货量，若不考虑缺货费用，虚拟产地Am+1到各个销售地的单位运费为零，否则就等于实际的缺货费用。如果要求某销售地不能缺货的话，那么虚拟产地Am+1到这个销售地的单位运费就设为一个非常大的正数M，这就保证了虚拟产地Am+1的虚拟产量am+1不能运输到该销售地。

通过以上处理，就可以将总产量小于总销量的不平衡问题转换为产销平衡的运输问题，然后用表上作业法求解即可。

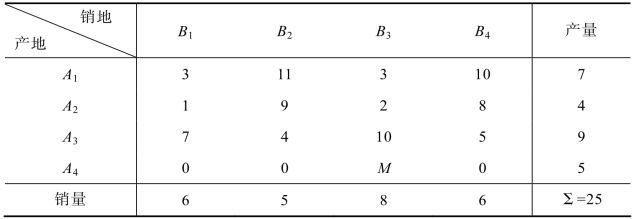
例5.4　表5.31是把产量、销量及单位产品运价整合在一起的某运输问题的综合表：

表5.31

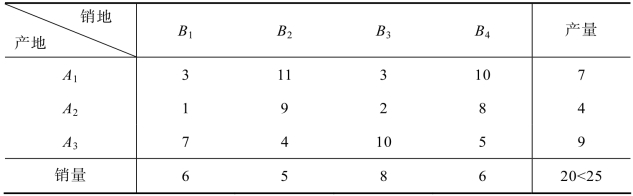
通过表5.31可以看出，产地的总产量为20，销售地的总销售量为25，产销不平衡，所以产销平衡的转换方法是虚拟一个产地A3+1，即增加一个产地A4，并令其产量a3+1为销量之和减去产量之和，即a4＝25-20＝5。假设不考虑缺货费用，则虚拟产地A4到四个销售点的单位运费为零，这样就可以构造出此运输问题的平衡表，如表5.32所示：

表5.32是运输问题的平衡表，用表上作业法求解即可。

表5.32

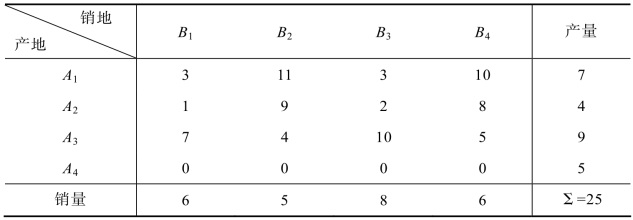
另外，再假设销售地B3不能缺货，那么虚拟产地A4到销售地B3的单位运费就设为一个非常大的正数M，这就保证了虚拟产地A4的虚拟产量a4不能运输到销售地B3，构造的平衡表如5.33所示：

表5.33

特别提示

由第2.4节单纯形法对线性规划模型解的判定可以知道，如果最优解中含有人工变量，则说明线性规划模型无可行解。但在运输问题中，如果最优解的基变量里含有虚拟产地或虚拟销售地的虚拟运量，则不能说此运输问题无可行解。通过上面两种不平衡运输问题的讨论也可以看出这样的结论，其实定理5.3已经给出了运输问题解的结论。