针对目标函数是min型的线性规划问题，单纯形法通过检验数cj－zj的非负情况来判断基本可行解是否已经达到最优解，而表上作业法对最优解的判断原则以及解的调整思路和单纯形法一样，不过调整方法和过程有所不同。

因为运输问题的目标函数是min型，所以表上作业法对最优解的判断原则仍然是检验数cj－zj全部大于等于0才说明达到最优解，如果有负的检验数存在，则说明没有达到最优解，需要进行解的调整。解的调整思路仍然是先确定换入变量，再确定换出变量，但换入变量和换出变量的确定方法以及调整过程和单纯形法不同。

由定理5.4可知，非基变量和一组基变量可以组成一个唯一的闭回路，如果某个非基变量要进入基变量中，这个非基变量的取值则由原来的0变为大于0的数。在上一节的闭回路法中已经解释过，在表上作业法的综合表中，每行和每列所分配的运量之和应该是一个常数，即分别等于产地的产量和销售地的销量，因此一旦给某个非基变量分配了运量，就会引起这个闭回路中所有顶点对应的基变量的值发生变化。为了保持行和列中量的平衡，有的基变量值需要增加，而有的基变量值则需要减小，但增加的量一定要等于减小的量，所以最终能增加多少则受制于最多能减少多少，但运量最大只能减小到0，不能出现负值。

基于定理5.4所说的闭回路，在顶点对应的基变量中，哪些基变量的值应该增加，哪些基变量的值应该减小；另外，增加的需要增加多少，减小的又需要减少多少，为了理解这些问题，下面结合图形5.4来进行简单的说明：

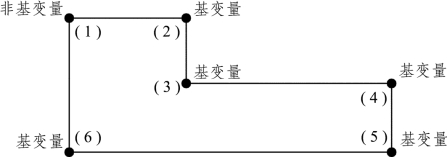
图5.4

可以看出，若非基变量成为换入变量，其值就由0增加为大于0的正数，为了保持行中所分配的运量之和等于产地的产量，顶点（2）处基变量的值就要减小相应的量值；同时为了保持列中所分配的运量之和等于销售地的销量，顶点（6）处基变量的值就要减小相应的量值。以此类推，可以知道，顶点为奇数的（1）、（3）、（5）处所对应的基变量的值就要增加，顶点为偶数的（2）、（4）、（6）处所对应的基变量的值就要减小。另外，为了保证减小的基变量的值不能成为负数，量值就应该等于偶数顶点中基变量的最小值。

基于以上分析，下面给出表上作业法解的调整步骤：

第一步：确定换入变量。

与单纯形法一样，在所有的负检验数中，一般选取检验数最小的非基变量作为换入变量。

第二步：确定换出变量和调整量。

由定理5.4可知，由此时还是非基变量的换入变量和一组基变量可以组成一个唯一的闭回路，找到这个闭回路以后，以此非基变量为起点，取此闭回路中偶数顶点取值最小的基变量作为换出变量；调整量的量值即为此基变量的值。

第三步：调整方法。

（1）闭回路以外的变量取值均保持不变。

（2）针对闭回路，奇数顶点变量的值全部加上调整量，偶数顶点变量的值全部减去调整量。

第四步：标识方法。

为了保证基变量的个数为m+n-1个，在标识上作如下处理：

（1）调整后，原来作为非基变量的换入变量就变成了基变量，所以要把这个变量的值标识成“○”。

（2）调整后，原来作为基变量的换出变量就变成了非基变量，所以要在这个变量的位置打上“×”。

第五步：继续求检验数，如果存在负的检验数，就返回第一步，否则计算停止，说明找到了最优解。

下面以求检验数过程中的表5.25为例，说明表上作业法的调整过程。(www.daowen.com)

解　在表5.25中，有负的检验数存在，说明当前的基本解还不是最优解。

第一步：综合表中只有x24的检验数为负值，所以将x24作为换入变量。以x24为起点的闭回路如表5.26所示：

表5.26　例5.1的综合表

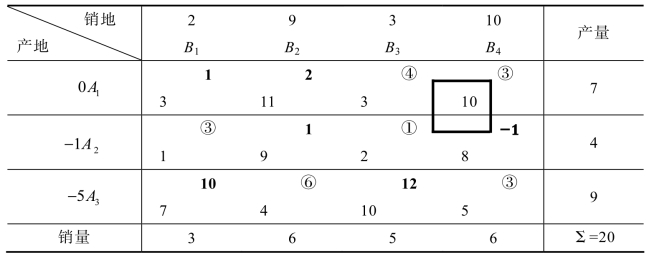
第二步：在闭回路的偶数顶点中，取值最小的x23=1，即x23作为换出变量，调整量的取值为1。

第三步：将综合表闭回路中奇数顶点的变量x13、x24的值加上调整量1，偶数顶点的变量x14、x23的值减去调整量1，并将x24的标识打成“○”，将x23的位置打成“×”，如表5.27所示：

表5.27　例5.1的综合表

第四步：对表5.27用闭回路法或位势法继续求检验数，得到表5.28：

表5.28　例5.1的综合表

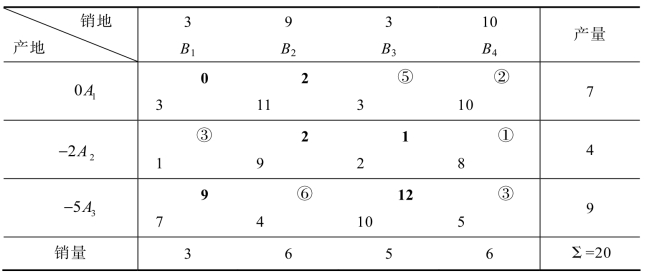
表5.28没有负检验数，说明已经找到最优解

(x13,x14,x21,x24,x32,x34)=(5,2,3,1,6,3)

则目标函数值z=3×5+10×2+1×3+8×1+4×6+5×3=85。

特别提示

（1）定理5.3说明了产销平衡的运输问题必定存在最优解，那么运输问题可能存在唯一最优解，也有可能出现多重解。对于多重解的判断和单纯形法一样，若出现非基变量的检验数为0，那么就有多重解。如综合表5.28中x11的检验数为0，说明例5.1的运输问题有多重解。将检验数为0的非基变量作为换入变量，以此作闭回路，按照调整规则找出换出变量，从而得到另一个最优解。

（2）运输问题有可能出现退化现象，对于退化现象的判断和单纯形法一样，即如果出现基变量的取值为0，则说明运输问题有退化解。出现退化现象的原因，是为了保证运输问题有m+n-1个基变量，有可能把取值为0的变量也要打上“○”，即将此变量标记为基变量。

（3）如果遇到目标函数是max型的特殊运输问题，用表上作业法求解时，可以令bij＝M-cij，其中M是足够大的常数，这样，目标函数就变为

由M是足够大的常数可知，bij≥0，所以使新目标函数达到最小的最优解即为原目标函数达到最大的最优解。