求初始基本可行解的方法有西北角法、最小元素法和差值法，在学习这三种方法之前，先给出相关知识、闭回路定义及有关的定理。

相关知识　运输问题有m+n个约束条件方程，有m×n个变量，而在运输问题约束条件方程组的系数矩阵中，前m个约束条件方程相加，正好得出一个与后n个约束条件方程相加完全相同的方程，这就说明约束条件方程组系数矩阵的行是线性相关的。也就是说，约束条件方程组中有一个方程是多余的，即起作用的约束条件方程只有m+n-1个，所以运输问题的基变量个数也只有m+n-1个。

在运输问题的m×n个变量中，面临着用什么样的方法找出哪些m+n-1个变量来组成基变量的问题，所以下面给出闭回路的概念和有关的定理。

定义5.1　凡是能排列成下列形式的变量集合称为闭回路：

其中i1,i2,…,im+n -1互不相同，j1,j2,…,jm+n -1也互不相同，这里出现的变量称为这个闭回路的顶点。

对定义5.1的通俗解释就是，从一个起点出发，遵循行变列不变或列变行不变的原则到另外的点，最终又回到起点的路径就构成了闭回路。表5.5中的变量就构成了一个闭回路：

表5.5

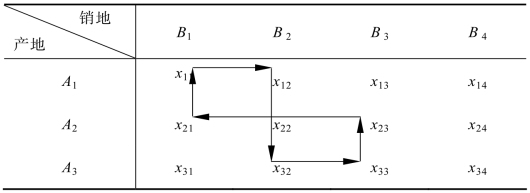
在上面的闭回路中，所有连线不是垂直就是平行，只有这样才符合行列一个变另一个不变的要求；连线不能是斜线，因为行列同时变化就出现了斜线。

闭回路有多种形式，如图5.1所示：

图5.1

定理5.1　m+n-1个变量能构成基本可行解的充分必要条件是它不含有闭回路。

利用前面的相关知识、闭回路定义5.1及定理5.1，就可求出运输问题的初始基本可行解。为了求初始基本可行解，需要解决以下三个问题：

（1）确定哪些变量作为基变量。

（2）在单纯形法中，基变量标识在单纯形表的第三列（即CB列），其余的变量作为非基变量，那么在表上作业法中，该如何标识基变量和非基变量。

（3）确定基变量的取值。

下面分别介绍运输问题求初始基本可行解的西北角法、最小元素法和差值法。

1.西北角法

西北角法，顾名思义，就是先从平衡表的西北角（即左上角）的位置开始标识基变量，依次进行，直到找到m+n-1个基变量为止。其具体步骤如下：

第一步：把单位产品运价表和平衡表整合到一张表中，将运价cij写在对应格子的左下角，运量xij写在对应格子的右上角，把这张表称为综合表，如表5.6所示：

表5.6　综合表

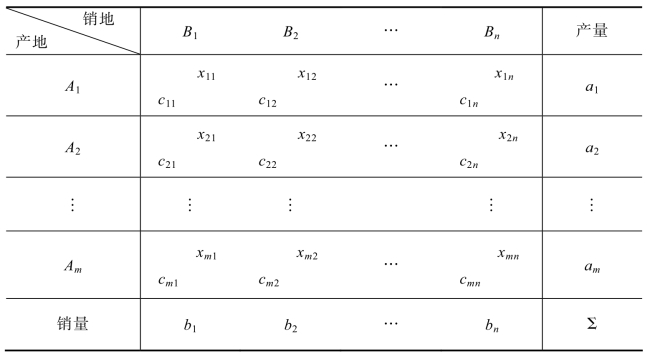
第二步：把左上角还没有标识的变量作为基变量。假设此基变量为xij，其取值可通过如下公式计算出来：

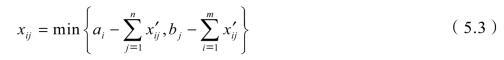
其中不包含xij，没有被标识的xij′值默认为0。记下xij值来自的行或列。

然后把基变量的取值打上“○”，即将该值对应的变量确定为基变量。

第三步：将xij值所来自的行或列中未标识变量的位置打上“×”，即将该位置上的变量标记为取值为0的非基变量。若xij值同时来自行或列，那么在行上打“×”后，就不能在列上打“×”，反之，在列上“×”后就不能在行上打“×”。

第四步：查看打“○”的基变量个数是否达到m+n-1个，若达到，说明已经找完初始基变量，计算停止，否则返回第二步。

下面对例题5.1用西北角法求初始基变量。

解　设决策变量xij表示由加工厂Ai运往销售地Bj的产品数量，此运输问题有m+n=3+4=7个方程，则应该有7-1=6个基变量。

第一步：构造综合表5.7：

表5.7　例5.1的综合表

第二步：现在左上角的x11还没有被标识，将x11变量作为基变量，x11取值可通过如下公式计算出来：

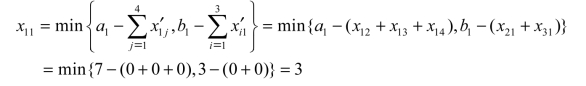
x11的值来自第1列，将基变量x11的值打上“○”。

第三步：将第1列中未标识变量x21、x31所在的位置打上“×”，即将x21、x31标记为取值为0的非基变量。处理后的综合表如表5.8所示：

表5.8　例5.1的综合表

第四步：表5.8中打“○”的基变量只有1个，还没有达到6个，继续寻找基变量。现在左上角x12没有被标识，将x12作为下一个基变量，x12取值可通过如下公式计算出来：

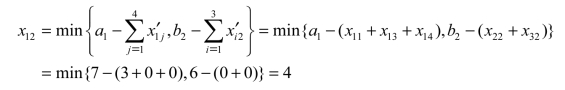
x12的值来自第1行，将基变量x12的值打上“○”。

第五步：将第1行中未标识的变量x13、x14所在的位置打上“×”，即将x13、x14标记为取值为0的非基变量，处理后的综合表如表5.9所示：

表5.9　例5.1的综合表

第六步：打“○”的基变量只有2个，还没有达到6个，继续寻找基变量。现在左上角x22没有被标识，将x22作为下一个基变量，x22取值可通过如下公式计算出来：

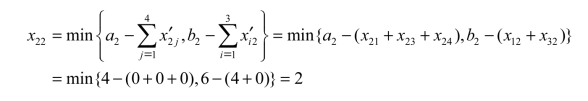
x22的值来自第2列，将基变量x22的值打上“○”。

第七步：将第2列中未标识的变量x32所在的位置打上“×”，即将x32标记为取值为0的非基变量，处理后的综合表如表5.10所示：

表5.10　例5.1的综合表

第八步：打“○”的基变量只有3个，还没有达到6个，依次用同样的方法，继续寻找基变量（其余过程省略），得出综合表5.11：

通过表5.11可以看出，打“○”的基变量已经达到6个，同时所有的变量已经标识完毕，即已经求出此运输问题的初始基本可行解

表5.11　例5.1的综合表

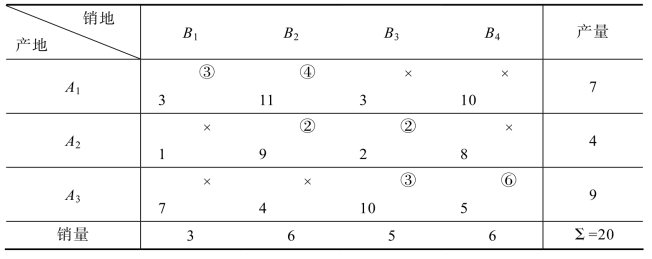
(x11,x12,x22,x23,x33,x34)=(3,4,2,2,3,6)

则目标函数值z=3×3+11×4+9×2+2×2+10×3+5×6=135。

通过以上例题的求解，对西北角法的求解过程有了具体的认识。但西北角法有其不足之处，因为西北角法只是满足了约束条件方程，而没有围绕目标函数来确定基变量及其取值，即没有考虑cij的值。若将cij考虑进去，那么得到的基本可行解就会使目标函数更优一些，即更接近最优解，从而使迭代的次数减少。为了弥补西北角法的不足之处，下面介绍运输问题求初始基本可行解的另一种方法——最小元素法。

2.最小元素法

最小元素法，不是先从综合表的左上角开始确定基变量，因为要求总运费最小，所以从没有被标识的变量所对应的最小运价处确定基变量。标识基变量、非基变量的方法以及基变量取值的确定和西北角法一样，直到找到m+n-1个基变量为止。(www.daowen.com)

最小元素法的具体步骤如下：

第一步：同西北角法一样构造综合表。

第二步：找出没有被标识的变量所对应的最小运价，如果最小运价有多个，就任意选择一个；把最小运价所对应的变量确定为基变量，其取值的确定和西北角法一样；将基变量的值打上“○”，即将该变量标记为基变量。

第三步：非基变量的确定方法和西北角法一样。

第四步：查看打“○”的基变量个数是否达到m+n-1个，若达到，说明已经找完初始基变量，计算停止，否则返回第二步。

下面对例题5.1用最小元素法求初始基变量。

解　第一步：构造综合表5.12：

第二步：在综合表5.12中，没有被标识的变量所对应的最小运价是c21=1，将x21作为基变量，取值和西北角法一样用公式（5.3）计算出来，即x21=3，再将x21的值打上“○”。非基变量的确定和标记与西北角法一样，处理后的综合表如表5.13所示：

表5.12　例5.1的综合表

第三步：在综合表5.13中，没有被标识的变量所对应的最小运价是c23=2，即将x23作为基变量，x23取值及标记、非基变量的确定和标记与西北角法一样，处理后的综合表如表5.14所示：

表5.13　例5.1的综合表

表5.14　例5.1的综合表

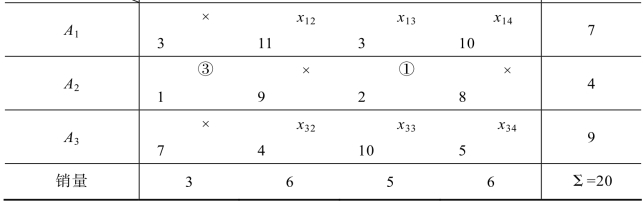
第四步：打“○”的基变量只有2个，还没有达到6个，用上面同样的方法继续寻找基变量（其余过程省略），得出综合表5.15：

通过表5.15可以看出，打“○”的基变量已经达到6个，同时所有的变量标识完毕，即已经求出此运输问题的初始基本可行解

表5.15　例5.1的综合表

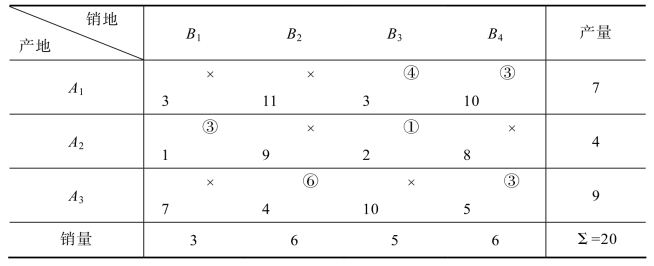
(x13,x14,x21,x23,x32,x34)=(4,3,3,1,6,3）

则目标函数值z=3×4+10×3+1×3+2×1+4×6+5×3=86。

由此可见，用最小元素法求出的目标函数值z=86比西北角法求出的目标函数值z=135要小的多，即用最小元素法求得的初始基变量更优一些。

通过以上求解，对最小元素法有了具体的认识，但最小元素法的缺点是，为了节省一个位置的费用，有可能要造成其他位置多花几倍的运费。下面介绍的运输问题求初始基本可行解的差值法，可以避免这样的问题。

3.差值法

某地产品若不能按最小运费就近供应，就考虑次小运费，这样就有最小费用与次小费用的一个差额。差额越大，说明不能按最小运费调运时，运费增加的就越多，因而对差额最大处就应当采用最小运费调运。标识基变量、非基变量的方法以及基变量取值的确定和西北角法一样，直到找到m+n-1个基变量为止。

差值法的具体步骤如下：

第一步：与西北角法一样构造综合表。

第二步：在综合表的最右边补一列，在最下面补一行。

第三步：依次找出综合表每行中没有被标识的变量所对应的次小运价和最小运价，并计算它们的差额，然后将差额填到新加的最右一列所对应的行中。

第四步：依次找出综合表每列中没有被标识的变量所对应的次小运价和最小运价，并计算它们的差额，然后将差额填到新加的最下一行所对应的列中。

第五步：从新加的最右差值列和最下差值行中选出最大的差值，若最大的差值有多个，就任意选择一个。

第六步：选择最大差值所在的行或列中没有被标识的变量所对应的最小运价，若最小运价有多个，就任意选择一个，这样选择可以避免将运量调配到同一行或同一列的次小空格中去。

第七步：把选择的最小运价所对应的变量确定为基变量，其取值的确定和标记与西北角法一样。

第八步：非基变量的确定和标记方法与西北角法一样。

第九步：查看打“○”的基变量个数是否达到m+n-1个，若达到，说明已经找完初始基变量，计算停止，否则返回第三步。

下面对例题5.1用差值法求初始基变量。

解　第一步：构造综合表，在综合表的最右边补一列，在最下面补一行，然后分别计算差值并填入表中，如表5.16所示：

表5.16　例5.1的综合表

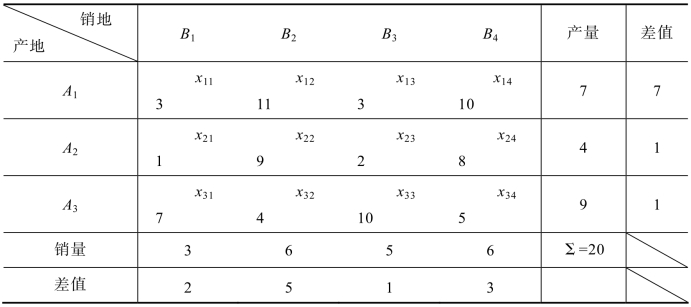
第二步：在表5.16中，最大差值7来自第一行，在第一行中没有被标识的变量所对应的最小运价是c11=c13=3，在这里选择变量x13作为基变量。x13取值同样和西北角法一样用公式（5.3）计算出来，x13=5，再将x13的取值打上“○”。非基变量的确定和标记同样与西北角法一样，处理后的综合表如表5.17所示：

表5.17　例5.1的综合表

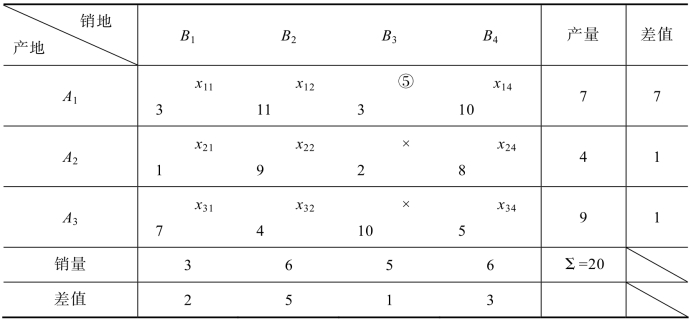
第三步：对表5.17重新计算差值，处理后的综合表如表5.18所示：

第四步：在表5.18中，最大差值7来自第一行和第二行，在这里选择第一行，第一行中没有被标识的变量所对应的最小运价是c11=3，计算出x11=2，将x11的取值打上“○”，处理后的综合表如表5.19所示。

表5.18　例5.1的综合表

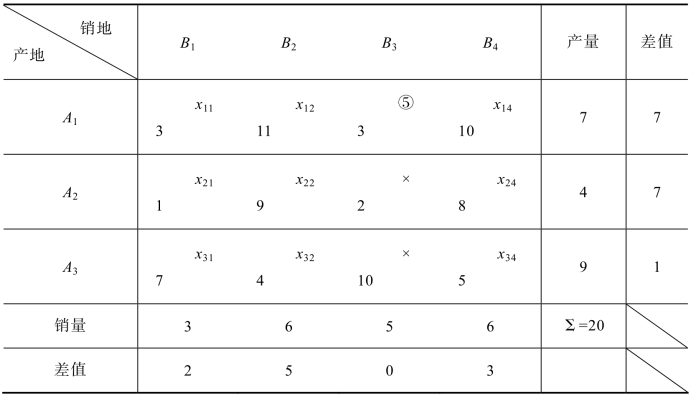
表5.19　例5.1的综合表

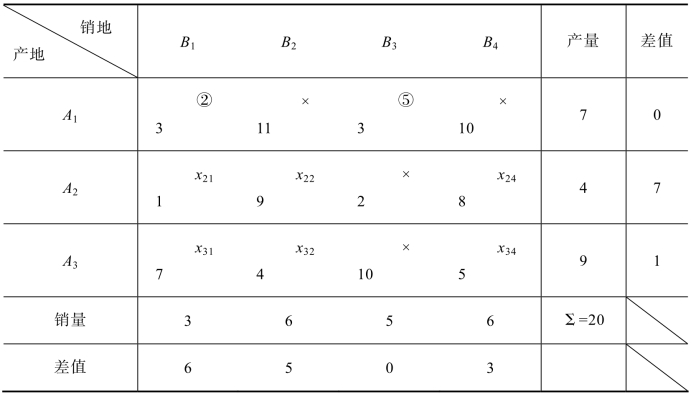
第五步：在表5.19中，打“○”的基变量只有2个，还没有达到6个，用上面同样的方法继续寻找基变量（其余过程省略），得出综合表5.20。

通过表5.20可以看出，打“○”的基变量已经达到6个，同时所有的变量标识完毕，即已经求出此运输问题的初始基本可行解

表5.20　例5.1的综合表

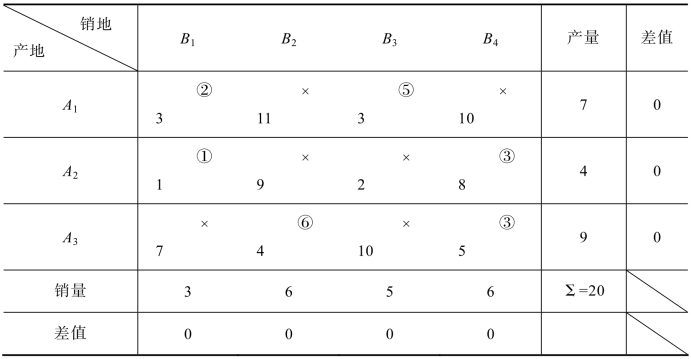
(x11,x13,x21,x24,x32,x34)=(2,5,1,3,6,3）

则目标函数值z=3×2+3×5+1×1+8×3+4×6+5×3=85。

基于以上求初始基本可行解的三种方法，可以给出下面两个定理：

定理5.2　用西北角法、最小元素法或差值法得到的xij值是一组基本可行解，打“○”位置对应的变量是基变量，打“×”位置对应的变量是非基变量。

定理5.3　运输问题一定有最优解。

证明　由定理5.2可知，运输问题一定有基本可行解。又因为运输问题的约束条件方程系数cij都是非负的，即可行解必定使运输问题的目标函数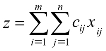永远取非负值。也就是说，至少还有一个z=0的下界存在，所以运输问题一定有最优解。定理5.3也说明了运输问题要么有唯一最优解，要么有多重解。

特别提示

无论是西北角法、最小元素法还是差值法，若打上“○”的基变量取值为0时，仍然保持打的“○”不变，目的是标识基变量的个数为m+n-1个。