1.运输问题线性规划模型描述

为了更好地了解运输问题及其模型结构，先给出以下引例。

例5.1　某公司有A1、A2、A3三个加工厂生产产品，产量分别为7吨、4吨、9吨，同时有B1、B2、B3、B4四个销售地，销量分别为3吨、6吨、5吨、6吨，从各工厂到销售地的单位产品运价如表5.1所示，设计该公司调运尽可能多的产品但总运费最少的方案。

表5.1　单位产品运价表

解　构建线性规划模型之前，先把产量、销量和单位产品运价表整合到一张表格中，如表5.2所示：

表5.2

通过给出的资料可知，三个加工厂的总产量为20吨，四个销售地的总销量也为20吨，把这种总产量与总销量相等的情况称为产销平衡，否则称为产销不平衡。

设决策变量xij表示从加工厂Ai到销售地Bj的产品数量，由单位产品运价列出目标函数，再根据三个产地和四个销售地分别列出约束条件方程，该问题的线性规划模型如下：

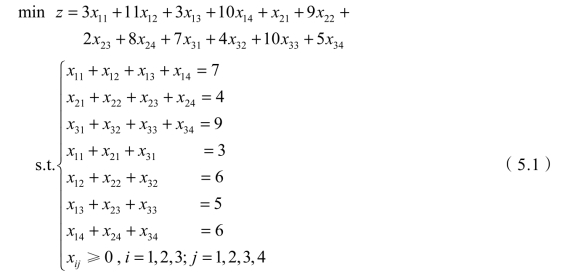
上面的模型就是已知各产地产量、各销地销量及产地销地之间单位运费，设计总运费最小的调运方案模型。针对这类特殊线性规划问题，下面给出通用的描述及模型形式。

例5.2　某公司有物资需要调运，该公司有m个产地A1、A2、…、Am，产量分别为a1、a2、…、am，有n个销售地B1、B2、…、Bn，销量分别为b1、b2、…、bn。在此先假设产地的产量之和等于销售地的销量之和，即该问题是产销平衡的。另外，从产地Ai到销地Bj的单位产品运价cij如表5.3所示。设计该公司调运尽可能多的产品但总运费最少的方案。

表5.3　单位产品运价表

解　设决策变量xij表示由第i个产地运往第j个销售地的产品数量，把产量、销量和决策变量整合到一张表格中，这张表称为平衡表，如表5.4所示：

表5.4　平衡表

需要说明的是，所谓的平衡主要是指产地的产量之和等于销售地的销量之和。另外，某个产地运出的总量应该等于该产地的产量，某个销售地接收的总量应该等于该销售地的销量。(www.daowen.com)

基于以上问题，总运费等于各个产地运往各个销售地的运费之和，即有

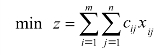
产地Ai运出的总量应该等于Ai的产量，则有；

销售地Bj接收的总量应该等于Bj的销量，则有；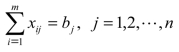

产地的产量之和等于销售地的销量之和，即产销平衡，则有。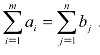

现在把上面问题的线性规划模型归纳如下：

这就是产销平衡运输问题的线性规划模型。除了经常遇到的物资调运之外，在其他活动中也会遇到此类问题。因为此类问题是从物资调运的运输问题而来，所以把具有模型（5.2）形式和特点的线性规划问题称为运输问题，也可称为标准运输问题。

2.标准运输问题线性规划模型的特点

通过观察运输问题的线性规划模型，可知其具有如下特点：

（1）标准运输问题的目标函数是min型。

（2）所有的约束条件方程（不包括非负约束）都是等式。

（3）它包含m×n个决策变量。

（4）由m个产地构建了前m个约束条件方程，由n个销售地构建了后n个约束条件方程，所以运输问题有m+n个约束条件方程。体现在平衡表中就是，一行对应一个方程，一列也对应一个方程。

（5）每一列正好有两个非零元素，即所有变量在前m个约束条件方程中各出现一次，在后n个约束条件方程也都各出现了一次，变量的系数元素非1即0。

（6）标准运输问题的前提条件是产量之和等于销量之和，即产销平衡。

运输问题显然是一个线性规划问题，也可以说是线性规划问题的扩展，是线性规划问题的分支，又可以认为是线性规划问题的应用，所以可以用单纯形法或对偶单纯形法求解。但是运输问题模型的类型比较特殊，结构又比较固定，若用上述两种方法求解，需要对每一个等式都加上一个人工变量（参考第2章当约束条件方程为等式时求初始基本可行解的方法），这样就会使变量的数量大大增加，从而使运输问题变得较为复杂，求解过程也变得比较繁琐。基于这样的原因，我们有必要用另外一种可行、简便的方法来求解，即在下一节将要介绍的运输问题的求解方法——表上作业法。