对bi值的灵敏度分析,就是在cj和aij不变的前提下,并在保证不改变原来最优解基变量但基变量取值可以变动的情况下,求出bi值的允许变动范围,即求出bi变动的上下限。
根据以上定义,bi值灵敏度分析的基础是:
(1)所谓不改变原来最优解的基变量,即基变量的组成保持不变。
(2)尽管基变量的取值可以变动,但基变量的新值必须满足非负约束。若基变量的新值不满足非负约束,说明bi的变动超出了范围。
基于以上的基础描述可知,bi值的变化仅仅影响基变量的取值。同时由第2.1.5节线性规划问题的典式可以知道,原来的资源b=(b1,b2,…,bk,…,bm)T,经过初等变换以后,变为b′=(b1′,b2′,…,bk′,…,bm′)T=B-1b,所以基变量
![]()
又知
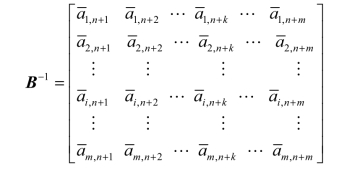
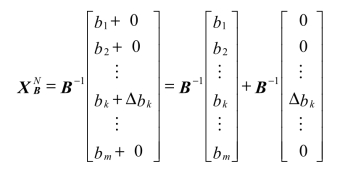
设bk的变化量为Δbk,则bN=(b1,b2,…,(bk+Δbk),…,bm)T,则bk变化以后基变量的新值为
![]()
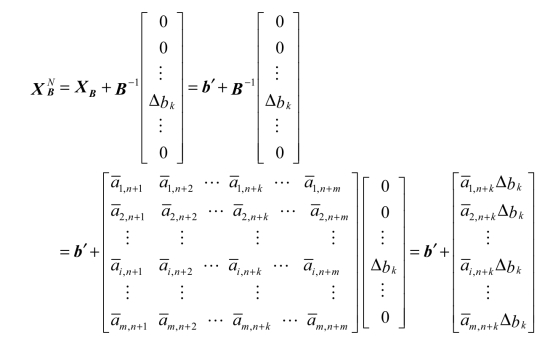
此式整理为
由XB=b′=B-1b可以有:
由可行性可知![]() ,所以有
,所以有
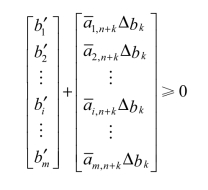
即有![]() 。
。
所以当![]() 时,有
时,有![]() ;当
;当![]() 时,有
时,有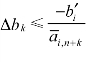 。因此针对所有的m个约束条件方程来说,变化量Δbk的取值范围是:
。因此针对所有的m个约束条件方程来说,变化量Δbk的取值范围是:
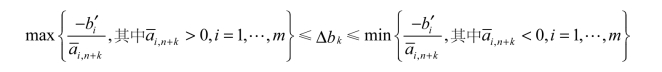
则bk值的允许变动区间为
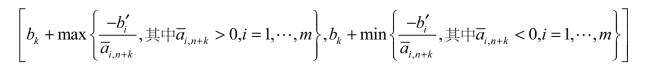
由前面的分析基础可知,当bk在允许变动区间变化时,基变量的取值会发生变化,即最优解发生了变化,此时不必对问题重新求解,可以由下式直接计算新的最优解:
![]()
如例4.1中,n=3,b2的变化量Δb2的取值范围就是:

即-12≤Δb2≤20。则b2值的允许变动区间就是[b2-12,b2+20],即[120-12,120+20]。也就是说,当b2在[108,140]内取任意值时,线性规划模型(4.1)最优解的基变量始终是x1、x2、x3,但基变量的取值会发生变化。假设取Δb2=10,原来最优解的基变量XB=(x1,x2,x3)=(5,25,15),列向量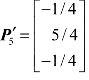 ,则最优解基变量的新值为
,则最优解基变量的新值为
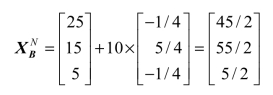
此时目标函数值zN=40×5/2+45×45/2+24×55/2=1772.5,比原来增加87.5。其实,目标函数值的增加量也可以由b2的边际值求出。由上可知,q2=z3+2=z5=35/4,则目标函数值的增加量为10×35/4=87.5。(https://www.daowen.com)
特别提示
当bi在允许范围内变动时,不会改变基变量的组成,但基变量的取值会发生变化,同时目标函数值也有可能发生了改变。
下面基于例3.1给出灵敏度分析的一个应用示例:
例4.2 某企业计划生产Ⅰ、Ⅱ两种产品,已知生产单位产品所需要的原材料A和B、资源量的消耗以及设备台时分别如表4.3所示:
表4.3
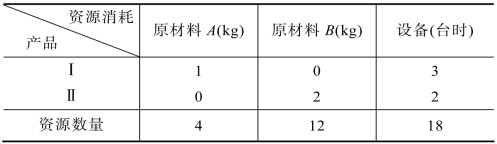
该工厂每生产一件产品Ⅰ获利3元,每生产一件产品Ⅱ获利5元。设x1、x2分别表示Ⅰ、Ⅱ两种产品的产量(在此假设产品小数),建立的线性规划模型如下:
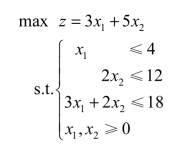
求解后的最优单纯形表如表4.4所示。由最优单纯形表可知,Ⅰ、Ⅱ两种产品的产量分别是2和6,因此获得的最大总利润为z=3×2+5×6=36元。
表4.4
![]()
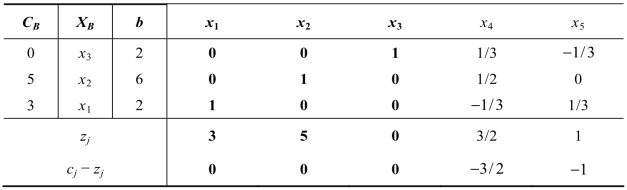
请解决以下问题:
(1)如果原材料B的数量增加到18 kg,那么新生产方案如何?利润比原来增加多少?
(2)如果企业通过工艺改进,使单位产品Ⅰ对原材料A的消耗由原来的1 kg减少到0.5 kg,这样的工艺改进是否使利润增加?如果企业工艺改进投入了2万元,另外,原材料A的市场价格为4万元,这样的工艺改进是否划算?为什么?
求解如下:
(1)增加原材料B的数量,就意味着对b2作灵敏度分析。根据bi灵敏度分析公式有
![]()
即有-6≤Δb2≤6,则b2的变化范围是[6,18]。当原材料B的数量增加了6 kg,即Δb2=6时,b2仍然在灵敏度变化范围内,新的最优解为
![]()
即新的生产方案为:Ⅰ产品的生产数量为0、Ⅱ产品的生产数量为9,新的最大总利润为3×0+5×9=45,总利润增加了45-36=9元。
另外,若求利润比原来增加多少,也可以用边际值计算,即
![]()
那么利润比原来增加了6×3/2=9元。
(2)问题所描述的其实就是对a11的灵敏度分析。a11对应的变量x1为基变量,根据aij灵敏度分析公式有-∞<Δa11<x3/x1,即有-∞<Δa11<1,那么a11的灵敏度变化范围是(-∞,2]。单位产品Ⅰ对原材料A的消耗由原来的1 kg减少到0.5 kg,没有超出a11的灵敏度范围,即没有改变最优解,所以不会使产品的利润增加。另外,尽管这样的工艺改进没有使利润增加,但还是带来了节省原材料A的好处。
产品Ⅰ节省的原材料A共计0.5 kg×2=1 kg,原材料A的市场价格为4万元,那么可以节
省费用4万元×1 kg=4万元。因为企业工艺改进投入了2万元成本,这样可有净收益4-2=2万元。因此这样的工艺改进尽管没有使产品的利润增加,但带来了间接的收益,从这个角度说还是划算的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






