对aij值的灵敏度分析，就是在cj和bi不变的前提下，并在保证不改变原来最优解基变量及其取值的情况下，求出aij值的允许变动范围，即求出aij变动的上下限。

根据以上定义，aij值灵敏度分析的基础是：

（1）由线性规划典式可知，aij值的变化对最优解的取值和检验数都会造成影响，但按照aij值灵敏度分析的定义，需要保持最优解不变，而保持最优解不变反应到最优单纯形表中，就是非基变量不能成为换入变量。

（2）若要保证非基变量不能成为换入变量，还要知道aij对应的变量xj是基变量还是非基变量。

基于以上的基础描述，若要分析aij值的允许变动范围，就要把aij对应的变量xj分为基变量和非基变量两种情况。

1.xj是基变量

若aij对应的变量xj为基变量，即xj在单纯形表的XB列，设aij的变化量为Δaij，又由单纯形表知道，单纯形表中每一行就对应一个约束条件方程等式，因此aij的变化会影响基变量的取值。假设第i个约束条件方程为

不妨令xn+i是松弛变量，则xn+i的取值有两种情况：

（1）xn+i=0的情况。

由ai1x1+…+aijxj+…+ainxn+xn+i=bi可知，资源bi已全部被使用，即bi全部用于其他基变量取值。此时有：

① 若aij增加，即Δaij>0，为了保持约束条件方程为等式，同时也为了满足基变量取值不变的要求，xn+i只有减少，即xn+i由0变为负值，但这样就造成xn+i不可行，所以aij不能增加。

② 若aij减小，即Δaij<0，和上面同样的原因，xn+i必须增加，即xn+i由0变为正值，这样xn+i就会变成基本量，从而改变了最优解的结构，但这又不符合aij值灵敏度分析的定义，所以aij也不能减小。

基于以上的分析，当xn+i=0时，即aij对应的资源bi全部被用完时，变化量Δaij的取值就是Δaij=0，则aij的值不允许变动。

（2）xn+i≠0的情况。

若xn+i≠0，说明xn+i是基变量，因为xn+i是松弛变量，也就说明资源bi没有被全部使用，即资源bi没有全部分配给有实际意义的决策变量，而是有一部分资源分配给了现实不存在的虚拟变量，即分配给了松弛变量xn+i。此时有：

① 若aij减小，即Δaij<0，为了保持约束条件方程为等式，同时也为了满足基变量取值不变的要求，xn+i只有增加，即xn+i取值在原来的基础上变大，仍然满足可行，而且还不改变最优解结构；又因为xn+i对应的目标函数系数cn+i=0，也不会改变目标函数值，所以aij可以任意减小，即-∞<Δaij。

② 若 aij增加，即Δaij>0，和上面同样的原因，xn+i必须减小，但xn+i不能减小到负数，否则xn+i不满足可行；又因为xn+i是松弛变量，所以没用完的资源数量就是xn+i的值，则有Δaijxj≤xn+i，即Δaij≤xn+i/xj。

基于以上分析，当xn+i≠0时，即aij对应的资源bi没有被全部使用时，变化量Δaij的取值范围就是-∞<Δaij≤xn+i/xj，则 aij 值的允许变动区间就是。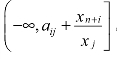

在例4.1中，a23对应的变量x3为基变量，其中x3+2=x5=0，所以a23的变化量Δa23=0，即a23的值不允许变动。

针对例3.1中模型（3.1）的最优单纯形表3.2来说，a12对应的变量x2为基变量，其中x2=6。另外，x2+1=x3=2，即x3≠0，所以变化量Δa12的取值范围就是-∞<Δa12≤x3/x2，有-∞<Δa12≤2/6，即-∞<Δa12≤1/3，则a12值的允许变动区间就是(-∞,a12+1/3]，即(-∞,0+1/3]。也就是说，当a12在(-∞,1/3]内取任意值，线性规划模型（3.1）的最优解不会改变。(www.daowen.com)

2.xj是非基变量

若aij对应的变量xj为非基变量，即xj=0，说明xj不在单纯形表的XB列，所以aij的变化不会影响基变量的取值，但会影响变量xj自身的机会费用和检验数。这种影响有两种情况：

（1）aij增加，即Δaij>0的情况。

由第i个约束条件方程ai1x1+…+aijxj+…+ainxn+xn+i=bi和xj=0可知，无论资源bi是否被全部用完，即xn+i无论是否等于0，aij增加不会影响基变量的取值，即不改变可行性。但是，aij增加会使机会费用zj越来越大，针对目标函数是max型时，只会使检验数时刻都能满足最优检验，即不会改变最优解，所以aij增加没有限制，即0≤Δaij<+∞；针对目标函数是min型时，aij增加同样没有限制，即0≤Δaij<+∞。

（2）aij减小即Δaij<0的情况。

aij减小会使机会费用zj越来越小，这样可能使检验数不满足最优检验，从而造成非基变量xj变成换入变量，所以aij不能无限制的减小。由边际值知识可知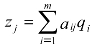，设，用表示新的机会费用，基于公式（4.2）则有

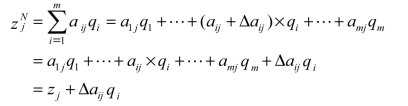
为了保证aij减小以后使检验数满足最优检验，aij值减小的情况分别有：

① 当目标函数是max型时，必须保证非基变量的检验数，则有：即。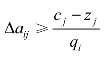

② 当目标函数是min型时，必须保证非基变量的检验数cj－zjN≥0，即有：

即。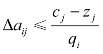

根据以上分析，变化量Δaij的取值范围及aij允许变动区间分别是：

① 目标函数是max型时，变化量Δaij的取值范围是，aij值的允许变动区间是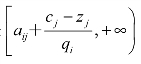。② 目标函数是min型时，变化量Δaij的取值范围是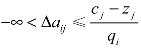，aij值的允许变动区间是。

在例4.1中，a24对应的变量x4为非基变量，所以变化量Δa24的取值范围为(c4－z4)/q2≤Δa24<+∞，有(-23/4)/(35/4)≤Δa24<+∞，即-23/35≤Δa24<+∞，则a24值的允许变动区间就是[a24+(-23/35),+∞），即[0+(-23/35),+∞）。也就是说，当a24在[-23/35,+∞）内取任意值，线性规划模型4.1的最优解不会改变。

同样，针对例3.1中模型（3.2）的最优单纯形表3.3来说，a11对应的变量y1为非基变量，所以a11的变化量Δa11的取值范围就是-∞<Δa11≤(c1-z1)/q1，有-∞<Δa11≤2/2，即-∞<Δa11≤1，则a11值的允许变动区间就是(-∞,a11+1]，即(-∞,1+1]。也就是说，当a11在(-∞,2]内取任意值，线性规划模型（3.2）的最优解不会改变。

特别提示

（1）当aij在允许范围内变动时，最优解不会改变。另外，目标函数值也不会改变，因为尽管aij发生了变动，但目标函数中所有的cjxj项的取值没有变动。

（2）针对aij值灵敏度分析的定义需要说明的是，所谓“不改变原来最优解基变量的取值”，确切地说应该是“不改变原来最优解基变量中决策变量的取值”，这一点从xn+i≠0的情况分析中可以看出。