在灵敏度分析中，涉及边际值和影子价格两个相关概念，在这一节首先给出这两个定义，并解释如何从单纯形表中找出它们的取值，同时结合例题说明它们的应用情况。

将第i种资源（第i行约束条件方程右端的值bi）从现在的用途中抽取1个单位以后，使目标函数减少的量值称为第i种资源的边际值，用qi表示。其中所谓现在的用途是指在有限的资源下生成的基变量及取值。

将第i种资源（第i行约束条件方程右端的值bi）增加1个单位时，最优目标函数值增加的量值称为第i种资源的影子价格，也可用qi表示。

为了便于理解边际值和影子价格的应用，同时为了方便对三个参数的灵敏度分析，现给出以下例题。

例4.1　某企业用钢、铝、铁生产3种产品A、B、C，有关资料如表4.1所示：

表4.1

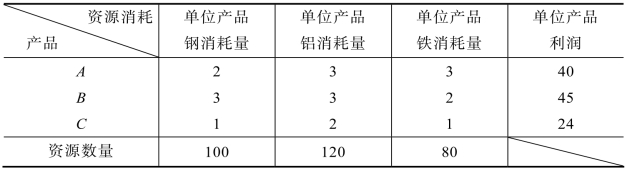
设x1为A产品的产量，x2为B产品的产量，x3为C产品的产量，每天生产产品A、B、C各为多少时使利润最大的线性规划模型为

表4.2是用单纯形法对该模型求解时的最优单纯形表。

表4.2

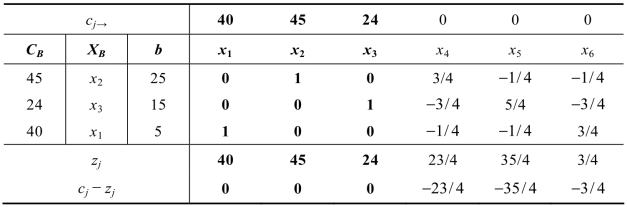
由表4.2得到最优解为(x1,x2,x3,x4,x5,x6)=(5,25,15,0,0,0），即最佳生产方案是产品A、B、C分别生产5、25、15个单位时，总利润最大z=40×5+45×25+24×15+0×0+0×0+0×0=1685。

用Δki表示抽取1个单位第i种资源以后，使第k个基变量xk变动的数值，则有Δki=xk－xk′，若Δki>0，表示xk的值是减少的，若Δki<0，表示xk的值是增加的。

下面分别对抽取1个单位的钢资源、铝资源、铁资源的情况进行分析：

（1）抽取1个单位的钢资源。

抽取1个单位的钢资源，就是使b1减少一个单位。从上面的最优单纯形表可以知道，此时必须使基变量x2、x3或者x1变动，才能保证最优单纯形表中第一个约束条件方程为等式。上面例题中，若x2减少1个单位，损失利润c2=45；x3减少1个单位，损失利润c3=24；x1减少1个单位，损失利润c1=40，所以损失总利润为c2×Δ21+c3×Δ31+c1×Δ11。通过边际值的定义可知

可以表示为　q1=(c2,c3,c1)[Δ21,Δ31,Δ11]T

现在只需求出Δ21、Δ31、Δ11的值，就可求出边际值q1。

由例题给出的资料可知，若产品B少生产一个单位，即基变量x2减少1个单位，可节约3个单位的钢、3单位的铝和2个单位的铁；若产品C少生产一个单位，即基变量x3减少1个单位，可节约1个单位的钢、2个单位的铝和1个单位的铁；若产品A少生产一个单位，即基变量x1减少1个单位，可节约2个单位的钢、3个单位的铝和3个单位的铁。由此可以列出方程组：

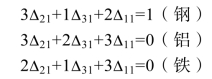
求解得出Δ21=3/4，Δ31=-3/4，Δ11=-1/4，则第1种资源（钢资源）的边际值为

（2）抽取1个单位的铝资源。

抽取1个单位的铝资源，就是使b2减少一个单位。和上面做同样的分析，有

(www.daowen.com)

也有方程组：

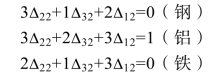
求解得出Δ22=-1/4，Δ32=5/4，Δ12=-1/4，则第2种资源（铝资源）的边际值为

（3）抽取1个单位的铁资源。

抽取1个单位铁资源，就是使b3减少一个单位。和上面做同样的分析，有

也有方程组：

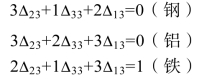
求解得出Δ23=-1/4，Δ33=-3/4，Δ13=3/4，则第3种资源（铁资源）的边际值为

由第2.1.5节线性规划问题的典式可以知道，在初始单纯形表中，初始基变量是松弛变量xn+i(i=1,2,···,m)，其初始系数列向量为Pn+i，迭代后其系数列向量变为-1 BPn+i。同时由公式（2.5）可知，zn+i=CB-1 BPn+i，所以qi=zn+i。

上式说明，某一个单纯形表中第i种资源（bi）的边际值qi等于该表中第i行约束条件的松弛变量xn+i的机会费用（同样适用影子价格）。也就是说，对边际值qi不必像上面例题那样分析求解，可直接由单纯形表读出。

在单纯形法中计算机会费用的公式为

在有了边际值的概念后，可用如下公式计算机会费用：

公式（4.2）的证明过程略。

下面通过示例解释边际值qi的另外一个应用。

在对线性规划模型求出最优解以后，如果建议生产一种新产品（即第2.5节新增加了决策变量的情况），设其产量为xN，相关参数设为aiN和cN，此时不必重新计算即可知道生产此种产品是否有利。因为xN要进入最优解，就必须有cN－zN≥0，再根据式（4.2）就可计算出新增加决策变量的检验数，从而可以判断新增加的决策变量能否成为基变量。

以第2.5节例2.10为例，假设有新产品，用x8表示新产品的产量，已知a18=5，a28=4，a38=3，c8=9，从最优单纯形表2.29可知，边际值分别为q1=0，q2=0.25，q3=1。由式（4.2）可计算出机会费用

x8的检验数c8-z8＝9-4＝5，为正，x8成为换入变量，所以应该存在使目标函数更优的解，故生产新产品有利。

另外的问题就是，如果生产新产品有利，那么如何求出新的最优解，这可参照第2.5节单纯形法的扩展应用（增加决策变量）的求解方法求解即可。

特别提示

当第i种资源（bi）的变化超出一定范围时，第i种资源的边际值qi要发生变动，即目标函数要发生变动。