通过例题以及对对偶单纯形法思路的了解，下面给出对偶单纯形法求解的具体步骤：

第一步：基于约束条件方程组的系数矩阵，通过寻找或构造单位矩阵的方法，找出满足最优检验的初始基本解，再利用初始可行解及线性规划模型提供的信息，编制初始对偶单纯形表。

第二步：查看所有的基变量是否存在负值，即检查基本解是否满足非负约束，若满足，则已求出最优解，计算停止，否则转到第三步。

第三步：继续迭代，使可行解中不满足非负约束的基变量个数减少，迭代过程如下：

（1）确定换出变量：原则上选择b列中负值最小的一行所对应的变量作为换出变量，若出现多个最小负值，任意取一个，把这一行标记为i*。

（2）确定换入变量：按照如下公式确定出最小值所在的列对应的变量作为换入变量。

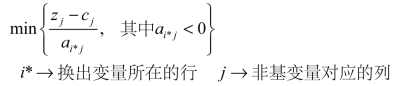
如果目标函数是max型，就将括号中的分子zj－cj改写为cj－zj。

（3）换出变量和换入变量确定后，生成另一张对偶单纯形表，即将单纯形表的换出变量和换入变量进行置换后，把CB列相应的目标函数系数变更，再对bi和aij的值进行初等变换，即进行行运算，从而将新基变量对应的矩阵调整为单位矩阵。

（4）重新计算机会费用zj和检验数cj－zj的值，返回第二步。

另外两种情况需要仔细考虑换出变量的问题：

（1）b列中负值最小的一行没有负ai*j，即所有的ai*j≥0，如对偶单纯形表3.10。

表3.10

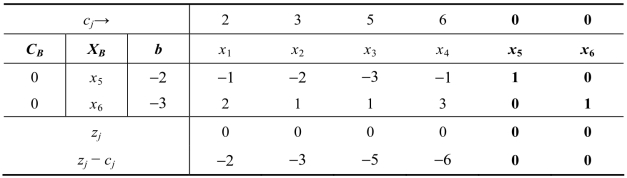
在单纯形表3.10中，b列中有两个取值为负的基变量，基变量x6的取值最小为3-，但所对应的行中，不存在负的ai*j，此时需要选择其他取值为负的基变量作为换出变量，如选择x5作为换出变量。

（2）b列中所有负值对应的所有行中都不存在负的ai*j，如对偶单纯形表3.11。

表3.11

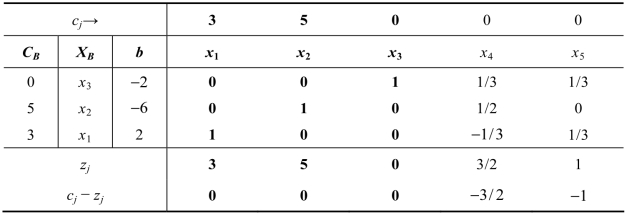
在单纯形表3.11中，b列中有两个取值为负的基变量x3、x2，但它们所在的行都不存在负的aij，这个现象表明此问题无解。

需要说明的是，在使用对偶单纯形法求解时，每次迭代计算都必须保证检验数满足最优检验，否则不能运用对偶单纯形法求解。

例如，下面这个模型就不能用对偶单纯形法求解：

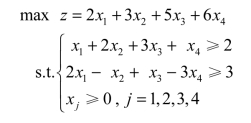
将模型化为

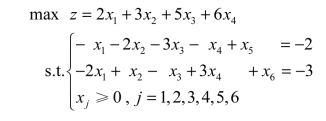(www.daowen.com)

其初始对偶单纯形表如表3.12所示。

表3.12

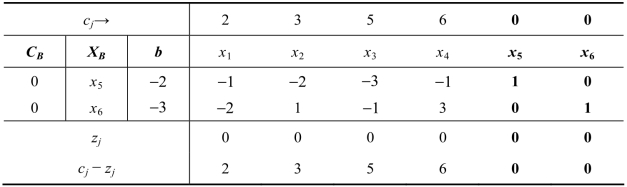
由表3.12可知，存在正的检验数，而模型为max型，没有达到对偶单纯形法求解时检验数满足最优检验的要求，所以此模型不能运用对偶单纯形法求解。

另外，对偶单纯形法并不是只对min型的模型求解，对有的max型的线性规划模型也可以用对偶单纯形法求解。

例如，下面这个max型的线性规划模型就可以用对偶单纯形法求解：

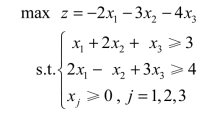
将上述模型转化为：

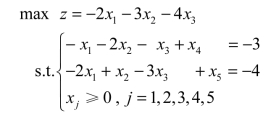
其初始对偶单纯形表如表3.13所示。

表3.13

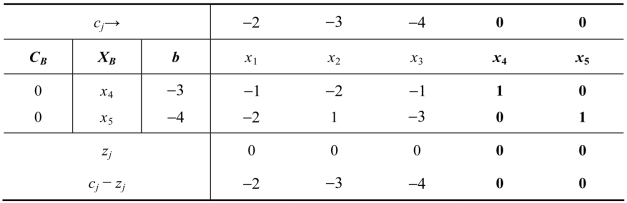
由表3.13可以看到，检验数全部保持小于等于0，满足最优检验，但b列中有负的基变量，不可行，需要继续迭代求解，下面直接给出最优的对偶单纯形表（见表3.14）。

表3.14

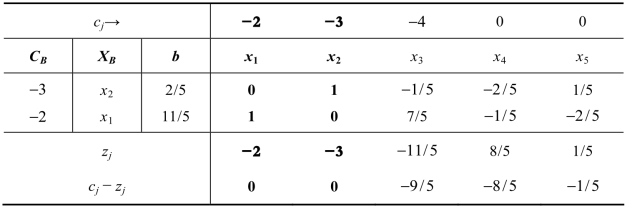
由表3.14可知，检验数仍然保持全部小于等于0，同时b列也全为非负，此问题的最优解为(x1,x2,x3,x4,x5)=(11/5,2/5,0,0,0）。

特别提示

（1）利用对偶单纯形法对线性规划模型求解时，模型中的所有变量都必须保证是非负的，但不必保证bi≥0。

（2）对偶单纯形法的显著优点是不需要引入人工变量，因此简化了计算。对于变量个数多于约束条件方程个数的线性规划问题，如果采用对偶单纯形法求解，会使计算量较少。

（3）对偶单纯形法是基于对偶理论来使用单纯形法对线性规划问题求解的一种方法，所以对偶单纯形法并不是只针对对偶问题来求解。

（4）使用对偶单纯形法求解时，对线性规划模型解的状态判断和单纯形法一样。

（5）在确定换出变量时，原则上选择b列中负值最小的一行所对应的变量作为换出变量，若选择其他负值对应的变量作为换出变量，也不会出现计算错误，但会造成迭代计算的过程麻烦一些。