基于上一节对对偶问题的了解以及原问题模型和对偶问题模型的对应关系，下面给出对偶理论的相关定理和性质。

不妨设原问题模型为

那么对偶问题模型为

1.对偶问题的对称性

定理3.1　对偶问题的对偶是原问题。

证明　将上述对偶问题模型（3.13）的目标函数转换为max型，同时把约束条件方程（非负约束除外）两边取负号，可以得到

很明显，式（3.14）和式（3.13）是等价的。根据建立对偶问题的规则，式（3.14）的对偶问题的模型为

对式（3.15）整理有

式（3.16）是式（3.13）对偶问题的模型，而式（3.13）又是式（3.12）对偶问题的模型，同时式（3.16）和式（3.12）是一样的，则对偶问题的对偶是原问题。

特别提示

根据对称性，可以把对称中的两个模型任选一个作为原问题，而另外一个就成为它的对偶问题。

2.对偶问题的弱对偶性

定理3.2　设是原问题（3.12）的可行解，Y是对偶问题（3.13）的可行解，则原问题的目标函数值不超过对偶问题的目标函数值，即CX≤bT Y。

证明　因为是原问题的可行解，则

用左乘此不等式，有

因为是对偶问题的可行解，有

现在用右乘此不等式，有

从而有

即有

所以

由定理3.2可以得出以下推论：

推论3.1　若原问题可行，但其目标函数值无界，则对偶问题不可行。也可以这样描述：若原问题为无界解，则对偶问题就无可行解。

证明　反证法，假设对偶问题可行，为对偶问题的可行解，则由弱对偶性的定理3.2可知，针对原问题的任意可行解，都有

即原问题的目标函数值有上界。这与问题中描述的原问题的目标函数值无上界矛盾，所以对偶问题不可行。

推论3.1的逆推论：若对偶问题不可行，则原问题的目标函数值无界。

类似地，利用弱对偶性的定理3.2，还可以得出其他的推论：

推论3.2　若对偶问题可行，但其目标函数值无界，则原问题不可行。也可以这样描述：若对偶问题为无界解，则原问题就无可行解。

推论3.2的逆推论：若原问题不可行，则对偶问题的目标函数值无界。

推论3.3　若原问题可行，而对偶问题不可行，则原问题的目标函数值无界。

推论3.4　若对偶问题可行，而原问题不可行，则对偶问题的目标函数值无界。3.可行解是最优解的性质

定理3.3　设X是原问题（3.12）的可行解，Y是对偶问题（3.13）的可行解，当CX＝bT Y时，和就分别是各自问题的最优解。

证明　由弱对偶性定理3.2可知，对偶问题的任意一个可行解Y都有

再由前提条件CX＝bT Y，有(www.daowen.com)

即，可见是使对偶问题（3.13）的目标函数取值最小的可行解，因此是最优解。同样也可以证明，对于原问题的任意一个可行解X，都有

再由前提条件CX＝bT Y，有

即，可见是使原问题（3.12）的目标函数取值最大的可行解，因此是最优解。

4.对偶定理

定理3.4　若原问题有最优解，那么对偶问题也一定有最优解，而且原问题与对偶问题的最优目标函数值相等。

证明　原问题是求目标函数最大，所以由线性规划模型典式中的式（2.5）和（2.6）可知，原问题的检验数为

经整理有

再设，把代入对偶问题（3.13）的目标函数中，有

设是原问题（3.12）的最优解，则根据线性规划模型典式中的式（2.3）可知，最优目标函

数为

由此得到

再由定理3.3可知，是对偶问题（3.13）的最优解，而且由上式也可以看出，原问题与对偶问题的最优目标函数值相等。

如果原问题的目标函数为min型，同样可以证明原问题与对偶问题的最优目标函数值都为bTCB B-1。

5.最优解的互读性

由定理3.4的证明过程及线性规划模型典式的生成过程可知，对偶问题（3.13）的最优解就是原问题（3.12）最优单纯形表中松弛变量对应的机会费用zs的值，或者说是原问题最优单纯形表中松弛变量对应的检验数cs－zs的负值，即yi=|zn+i|。

如果原问题的目标函数为min型，则对偶问题的目标函数为max型，对偶问题的最优解就是原问题最优单纯形表中多余变量对应的机会费用zs的负值，或者说是原问题最优单纯形表中多余变量对应的检验数cs－zs的值，即yi=－zn+i。

为了验证最优解的互读性，也为了探讨原问题的最优解与对偶问题最优解之间的联系，下面将例3.1的原问题及对偶问题的最优单纯形表分别列在表3.5和表3.6中。

表3.5　例3.1原问题的最优单纯形表

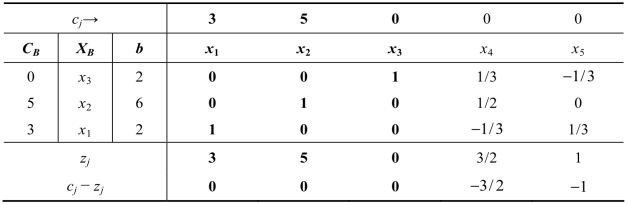
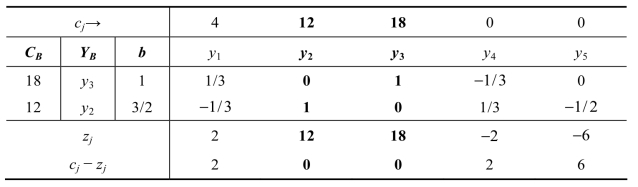
表3.6　例3.1对偶问题的最优单纯形表

对偶问题决策变量的最优解可以由原问题最优单纯形表3.5中读出，即

同理，原问题决策变量的最优解可以由对偶问题最优单纯形表3.6中读出，即

例3.3　分析下列线性规划模型的求解问题。

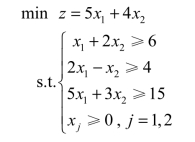
若对此模型求解，必须先引入三个多余变量将其化为等式，另外还要引入三个人工变量以构造单位矩阵，然后再用大M法或两阶段法求解，这样就造成变量大量增加，而且计算量也加大。

如果基于前面叙述的对偶理论，先对对偶问题进行处理和求解，再确定原问题的最优解，就解决了求解麻烦的问题。

下面写出对偶问题的模型：

要对此对偶模型求解，必须先引入两个松弛变量把约束条件方程化为等式。由于松弛

变量本身已构成了单位矩阵，所以直接用单纯形法求解，再利用对偶问题的最优单纯形表读出原问题的最优解即可。这样变量很少，计算量也很小。

从以上例题的求解分析可以看出，对目标函数是min型，约束条件方程存在“≥”的形式，就不必引入人工变量，直接对它的对偶问题求解即可。这也为这类线性规划问题的求解提供了另一种策略，但这种策略不是一个最优的求解思路，最优的求解思路之一是下一节要介绍的对偶单纯形法。

特别提示

（1）由对偶问题的对称性定理3.1可知，原问题的最优解也可以从对偶问题的最优单纯形表中读出。

（2）这里所说的最优解互读，主要是指最初线性规划模型中决策变量值的互读，而不是为了模型转换或为了求解而人为加进的其他变量。