对线性规划模型求出最优解以后，如果模型新增加了决策变量，就会导致原有的模型变成了一个新的模型。针对新模型，求解的一般思路是从头开始求解，但从原有模型的求解过程可知，初始单纯形表中初始基变量对应的矩阵是单位矩阵，而在最优单纯形表中，这个单位矩阵就变成了另外的矩阵。如果从初等变换的角度考虑，就相当于用某个矩阵乘了初始基变量对应的单位矩阵，从而使这个单位矩阵变成了另外的矩阵。对于新增加的决策变量来说，它的初始值已经给出，也就是说新增加的决策变量在初始单纯形表中的列向量是已知的，如果用同样的某个矩阵乘以新增加决策变量初始的已知列向量，就会得到新增加决策变量在最优单纯形表中的列向量，再把这个求出的列向量补加到最优单纯形表的最右列，继续求解即可。这样，对新模型就不必从头求解。

求解的主要步骤如下：

第一步：用IB表示初始单纯形表中初始基变量所对应的单位矩阵，再用IB*表示初始基变量在最优单纯形表中所对应的矩阵，基于线性规划模型的典式，可知

因为IB为单位矩阵，所以有B-1=IB*。用xn+1表示新增加的决策变量，那么它在初始单纯形表中对应的列向量是已知的，用Pn+1表示；再用P*n+1表示新增加的决策变量在最优单纯形表中应该对应的矩阵，则有

第二步：把列向量P*n+1补加到最优单纯形表的最右列，继续求解即可。

下面通过具体例题来说明新增加决策变量的求解步骤。

例2.10　某企业针对生产计划构建了如下的线性规划模型：

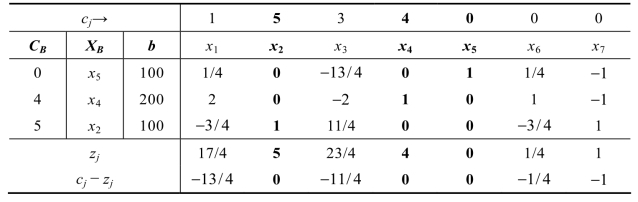
设x5、x6、x7是松弛变量，对该模型用单纯形法求解，得到最优单纯形表2.29。

表2.29

假设该企业研制了新产品，现在准备生产该新产品，已知该新产品耗用资源1为5，耗用资源2为4，耗用资源3为3，该产品的单位利润为9，请求新的最优生产方案。(www.daowen.com)

解　用决策变量x8表示新产品的生产数量，新决策变量使原有的模型变为

模型（2.16）与模型（2.15）可以说是完全不同的两个模型，对模型（2.16）求解的一般思路是从头开始求解。下面用前面的步骤进行求解。

针对模型（2.15），初始单纯形表中的基变量是x5、x6、x7，则有

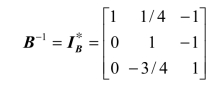
针对模型（2.16），新增加的决策变量x8在初始单纯形表中对应的列向量为

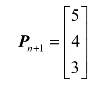
那么决策变量x8在最优单纯形表中的列向量即为

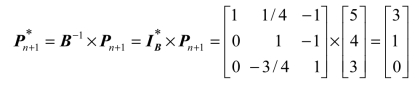
把这个列向量补加到最优单纯形表2.29的最右列，并计算机会费用和检验数，得表2.30。

表2.30

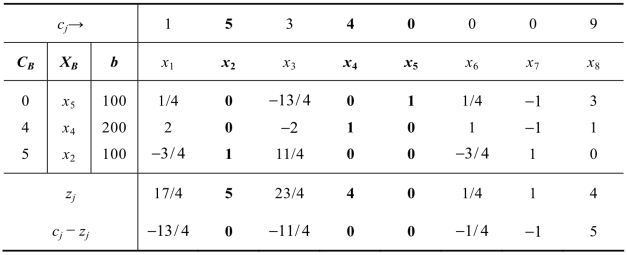
表2.30没有满足最优检验，将x8作为换入变量，由min{100/3,200/1}=100/3可知，换出变量为x5，继续迭代计算求最优解即可（求解过程省略）。