在第2.1.2节中，通过对线性规划模型解的状态分析可知，线性规划模型的解有唯一解、无可行解、多重解和无界解四种情况，另外，线性规划问题还会有退化现象出现。用单纯形法求解线性规划模型，最常见的是唯一解，而其他解的情况也能在最优单纯形表中反映出来。本节将介绍如何依据单纯形表来判断线性规划模型解的状态。

1.无可行解（不可行性）

在前面已经提到，如果线性规划模型的最优单纯形表中，基变量包含一个或多个非0的人工变量，那么该线性规划模型就没有可行解。也就是说，只有在采用实际不存在的虚拟活动时（附加人工变量），线性规划模型才仅仅有理论上的数学解，而这种情况使目标函数永远不能达到具有实际意义的最优。从几何意义的角度来说就是，约束条件方程组没有可行域，即约束条件方程组没有公共解。产生这种情况的原因是在建立数学模型时，列出了矛盾的约束条件方程。

在前面讲到，针对包含人工变量的线性规划问题，需要使用大M法或两阶段法求解，那么无可行解在大M法中体现的就是最优解基变量中含有非0的人工变量，而在两阶段法中体现的就是在第一阶段的最优解基变量中含有非0的人工变量，无法转入第二阶段。

例2.6　解如下线性规划模型：

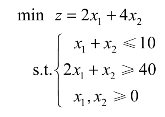
解　对第一个约束条件方程引入松弛变量x3，对第二个约束条件方程引入多余变量x4和人工变量x5，模型变为

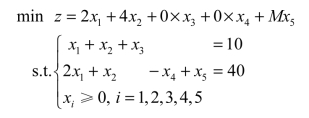
（i）用大M法求解（见表2.17）。

表2.17

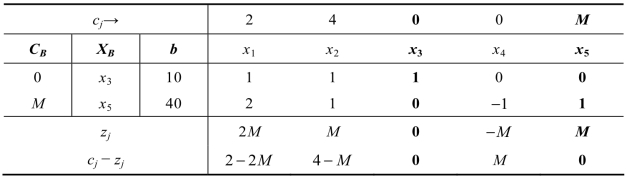
继续迭代求解，如表2.18所示。

表2.18

由上面的最优单纯形表可以看出，检验数全部大于等于0，但是基变量中含有非0的人工变量x5，即无法得到实际问题的基本可行解，因此这个线性规划模型无可行解。

（ii）用两阶段法求解，第一阶段的初始单纯形表如表2.19所示。

表2.19

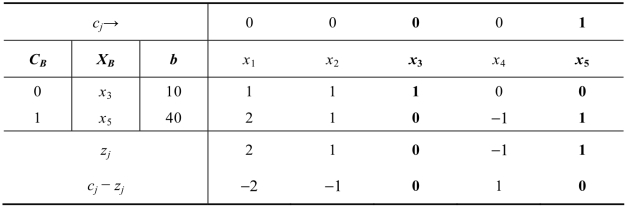
继续迭代求解，如表2.20所示。

表2.20

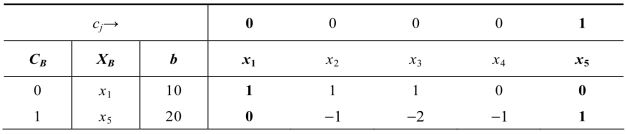
已经得到第一阶段的最优解，但最优解基变量中含有非0的人工变量x5，无法转入第二阶段，此模型无可行解。

2.多重解

在第2.1.2节线性规划模型解的状态分析中，已经讨论了多重解问题，下面以一个例题来继续讨论存在多重解时的特征。

例2.7　解如下线性规划模型：

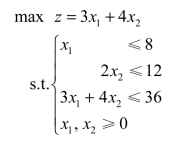
解　引入松弛变量x3、x4、x5，将模型化为标准型：

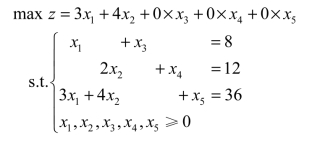
用单纯形法求解，得到最优单纯形表2.21。

表2.21

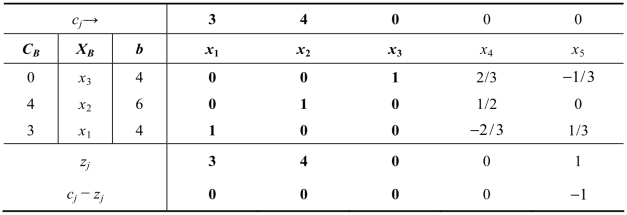
最优解为(x1,x2,x3,x4,x5)=(4,6,4,0,0)。通过观察发现，非基变量x4的检验数为0，不妨把x4作为换入变量再进行一次迭代，根据规则，x3确定为出换出变量，迭代之后的单纯形表如表2.22所示。

表2.22

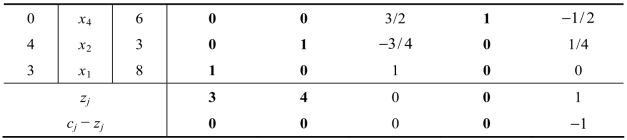
又得到另外一个最优解：(x1,x2,x3,x4,x5)=(8,3,0,6,0)。这样，同一个模型就出现了两个最优解，再利用第2.1.2节中多重解的讨论，就可以求出无穷个最优解：

基于上面例题的现象，可以得出结论：在最优单纯形表中，如果存在检验数为0的非基变量，线性规划模型就有多重解。或者说，在最优单纯形表中，如果出现检验数等于0的个数多于基变量的个数，那么线性规划模型就有多重解。(www.daowen.com)

3.无界解

在第2.2.1节单纯形法的求解思路中，判断基本可行解是否达到最优时，已经详细讨论了线性规划模型无界解的情况，即所有能作为换入变量所对应的系数列向量均不存在aij>0时，线性规划模型会出现无界解。无界解产生的原因可能是建立数学模型时所列的约束条件方程不适当。

例2.8　解如下线性规划模型：

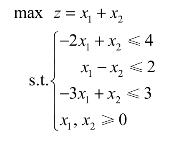
解　将模型化为标准型：

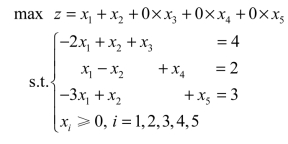
初始单纯形表如表2.23所示。

表2.23

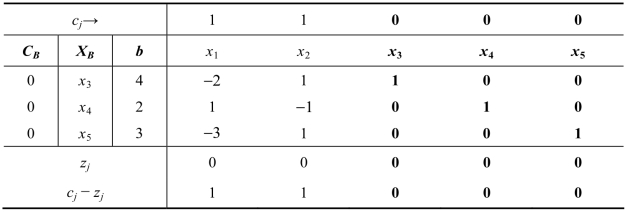
迭代求解，得到单纯形表2.24。

表2.24

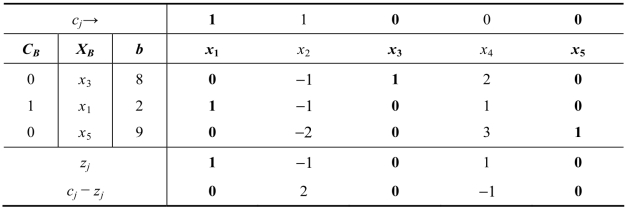
表2.24中非基变量x2的检验数为正数，应该作为换入变量，但所对应的列向量全部小于0，另外也没有其他非基变量可作为换入变量，所以此线性规划模型为无界解。

4.退化现象

已经知道，基变量的个数就等于约束条件方程的个数，然而，一般情况下，基变量不等于零，此时基本可行解中非零变量的个数就等于约束条件方程的个数。如果出现基变量等于零，就会造成基本可行解中非零变量的个数小于约束条件方程的个数，这就是退化现象。在用单纯形法求解时，退化现象表现为，若确定的换出变量同时有两个或两个以上，就会造成下一次迭代时有一个或几个基变量的取值为0。

退化现象是一个需要证明收敛的问题，退化是高等数学中的常用术语，它表示一个一般不为零的量变成了零的现象。如在求解方程时，如果只有零解，那么就说该方程有退化解。

为了证明单纯形法在有限次迭代中收敛于一个最优解，必须假定每次迭代都使目标函数值有所改进，但在退化现象中，有时的迭代就没有使目标函数值改进。这样从理论上讲，迭代可能会循环无限次，但实践证明没有发生此现象，即有时的迭代恰恰使目标函数有了改进，也很快收敛于最优解。下面通过例题来了解一下退化问题。

例2.9　解如下的线性规划模型：

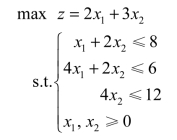
解　将模型化为标准型：

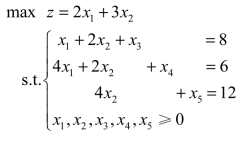
初始单纯形表如表2.25所示。

表2.25中非基变量x2作为换入变量，换出变量由下式确定：

表2.25

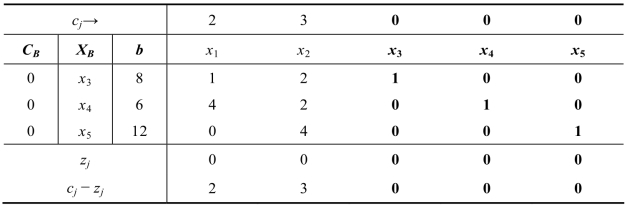
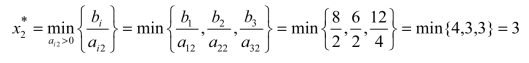
而最小值3来自第2行和第3行，换出变量可以是x4，也可以是x5，在此指定x5作为换出变量，继续迭代计算得到单纯形表2.26。

表2.26

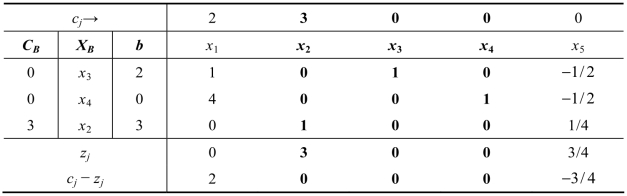
继续迭代计算，得到单纯形表2.27。

表2.27

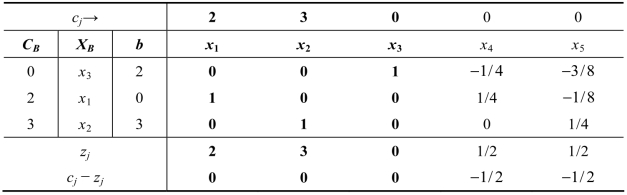
表2.27达到最优，最优解为(x1,x2,x3,x4,x5)=(0,3,2,0,0)，目标函数值z=2×0+3×3=9，最优解中基变量x1的值为0，这就是退化现象。

继续讨论一下，如果在表2.25中，不是指定x5，而是指定x4作为换出变量，继续迭代计算得到单纯形表2.28。

表2.28达到最优，最优解为(x1,x2,x3,x4,x5)=(0,3,2,0,0），目标函数值z=2×0+3×3=9，最优解中基变量x5的值为0。

表2.28

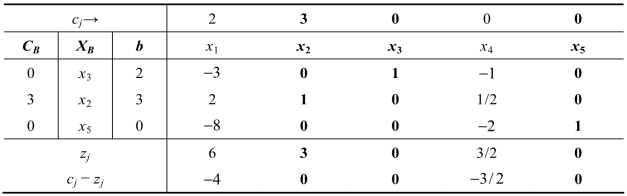
可以看出，换出变量取不同的x4和x5时，最优解中基变量的组成是不同的，但是最优解及其取值是一样的，所以目标函数值也是一样的。