在第2.2节中，基于线性规划问题的标准型讨论和分析了单纯形法的求解思路。另外，在给出的例题中，模型的约束条件方程全部都是“≤”的情况，即前面讨论的线性规划问题都是目标函数值最大、约束条件方程均为“≤”型的问题。

在本节中，主要讨论如何使用单纯形法对其他形式的线性规划模型进行求解，即目标函数值最小、约束条件方程为“≥”、约束条件方程为“=”型的线性规划问题。

1.目标函数值最小的问题（min型）

关于这类问题，有三种处理方式：

（1）在第2.1.3节中介绍过，可将求目标函数值最小的问题转化为求目标函数值最大的问题。如果目标函数是的形式，可令z＝-z′，这样就将目标函数转化为，然后用单纯形法求解即可。

（2）保持目标函数的min型不变，通过检验数的判断来处理。最优解的判断方法和max型相反，即全部检验数cj－zj≥0时就达到最优，否则继续迭代。另外，换入变量的确定方法是选取检验数最小的非基变量作为换入变量，确定换出变量的方法与max型一样。

（3）改变单纯形表中检验数的形式。即将单纯形表中的检验数cj－zj改写为zj－cj的形式，最优解的判断方法、换入变量的确定和换出变量的确定与max型相同。

2.约束条件方程为“≥”型的问题

在第2.1.3节中介绍过，可将“≥”型的约束条件方程左边减去多余变量即可转化为“=”型的约束条件方程。同时知道，确定初始基本可行解的方法是将单位矩阵所对应的变量作为基变量，但多余变量的系数是-1，不能构成单位矩阵，即不能将多余变量作为初始基变量。

如果在变化后的约束条件方程组的矩阵中找不到单位矩阵，解决的方法就是通过人为构造变量来生成单位矩阵，把人为构造的变量称为人工变量。为了不使人工变量对目标函数值产生影响，在求目标函数最大或最小的问题中，人工变量的cj值分别设为充分小或充分大的数，即-M或M，这样，人工变量进入最优解的可能性就很小。

另外，如果在约束条件方程组中有变量的列向量为单位列向量时，可以不必在有该变量的方程中再构建人工变量。如下例：

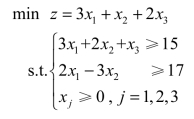
利用多余变量x4、x5把约束条件方程转换为等式，变量x3的列向量为单位列向量，就不必在第1个方程中再构建人工变量，只需要在第2个方程中构建人工变量x6即可。为了使人工变量x6不对目标函数值产生影响，c6的值设为充分大的数M，如下所示：

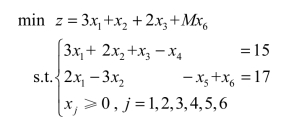
针对包含人工变量的线性规划问题求解，需要使用单纯形法的两种衍生方法：大M法、两阶段法。

例2.5　解如下线性规划模型：

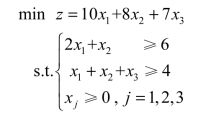
（i）用大M法求解。

将模型化为如下形式，其中x4、x5为多余变量，x6为人工变量：

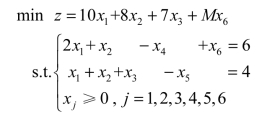
其初始单纯形表如表2.10所示。

表2.10

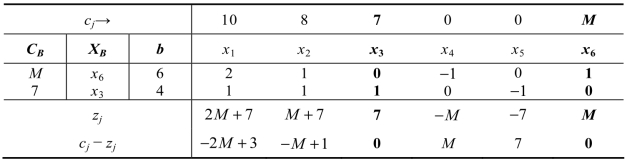
因为 M 是很大的数，同时表中的检验数 cj－zj 表明还没有达到最优解，又因为-2M+3<-M -1，所以把x1作为换入变量；因为6/2<4/1，所以把x6作为换出变量，得到单纯形表2.11。

表2.11

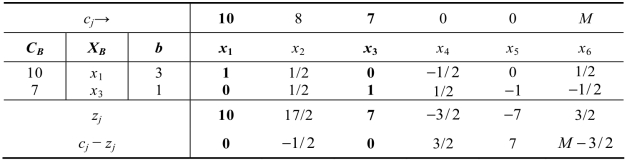
表2.11还没有达到最优解，继续迭代，得到单纯形表2.12。

表2.12已经达到最优解，求出的最优解为(x1,x2,x3,x4,x5,x6)=(2,2,0,0,0,0)，目标函数值为36。

表2.12

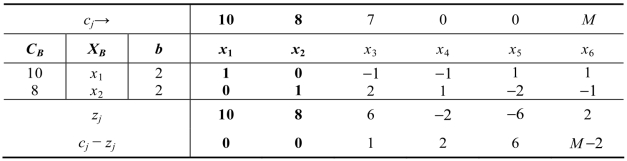
特别提示

大M法就是将加入了人工变量后的线性规划问题用单纯形法求解，其中有两点需要注意：

（1）由于运算所得的数字中含有大M，在计算检验数时还要求出差值，所以判别检验数的正负时要谨慎。

（2）如果已经满足了最优检验，但基变量中仍然含有人工变量，也就是说，只有人工变量取值不为零时，才能求出模型的最优解，这说明目标函数永远不能达到具有实际意义的最大或最小，所以该问题无可行解。

（ii）用两阶段法求解。(www.daowen.com)

顾名思义，两阶段法就是分两个阶段求解含有人工变量的线性规划模型。求解过程是：在第一阶段构造一个新的目标函数代替实际的目标函数，然后用单纯形法求解，直到满足最优检验并且基变量中没有人工变量时，再转入第二阶段；在第二阶段恢复原来的目标函数，继续用单纯形法求解。

（1）第一阶段：构造新的目标函数代替实际的目标函数，用单纯形法求解。

若目标函数是max型，可设人工变量的目标函数系数cj＝-1，其余变量的目标函数系数cj=0；

若目标函数是min型，可设人工变量的目标函数系数cj=1，其余变量的目标函数系数cj=0；

仍然以上面的例2.5为例，第一阶段的初始单纯形表如表2.13所示。

表2.13

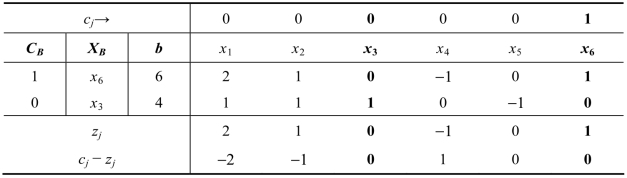
没有达到最优解，继续迭代，得到单纯形表2.14：

表2.14

上面的单纯形表已达到最优，并且基变量中没有人工变量，所以转入第二阶段。

（2）第二阶段：恢复原来的目标函数，继续用单纯形法求解。

恢复原来目标函数的步骤是：

① 将第一阶段最优单纯形表中人工变量的列去掉；

② 恢复原来的目标函数的系数；

③ 重新计算检验数，并继续用单纯形法求解。

表2.14变换为表2.15。

表2.15

没有达到最优解，继续迭代求解，得到单纯形表2.16。

表2.16

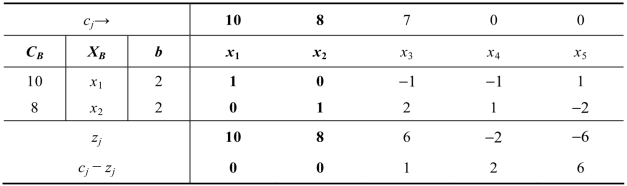
在表2.16中，除了没有x6列以外，得到的是和大M法一样的最优单纯形表。

特别提示

如果第一阶段结束后，基变量中仍然含有人工变量，那么就不能转到第二阶段，此时说明该问题无可行解。

3.约束条件方程为“=”型的问题

关于这类问题，有两种处理方式：

（1）在约束条件方程中加入人工变量，使系数矩阵能构成一个单位矩阵，再用大M法或两阶段法求解。

（2）将等式变为两个非等式，如x1+2x2=10可以用x1+2x2≤10和x1+2x2≥10这两个不等式来代替，这样变化后，可以在这两个方程中分别加进松弛变量、减去多余变量或者加入人工变量，再按照前面的方法求解即可。

特别提示

（1）无论对哪一种情况用单纯形法求解，都必须保证模型中bi≥0、xi≥0。

（2）构建人工变量的目的就是构造单位矩阵，从而确定初始的基本可行解。