单纯形法的基本思路：

（1）求出线性规划模型的初始基本可行解X(0)，利用初始基本可行解X(0)及线性规划模型提供的信息，编制初始的单纯形表。

（2）判断X(0)是否使目标函数达到最优，即X(0)是否为最优解。

（3）若X(0)是最优解，计算停止；若X(0)不是最优解，就将一个非基变量换入，同时将一个基变量换出，也就是说，将一个非基变量变成基变量，同时将一个基变量变成非基变量，从而产生另外一个使目标函数更优的基本可行解X(1)，然后生成另外一张单纯形表，再返回第（2）步。这个过程称为迭代过程，如此逐步迭代，如果线性规划模型有最优解，那么经过有限次迭代后就会求出最优解。

针对单纯形法基本思路的三个过程，需要解决以下几个问题：

（1）如何求初始基本可行解X(0)？

（2）判断基本可行解是否为最优解，需要建立一个判断的标准和方法，那么这个判断标准是什么？又用什么样的方法去判定？

（3）若基本可行解不是最优解，那么如何将一个非基变量换入？如何将一个基变量换出？又如何生成另外一张单纯形表？

为了解决以上问题，同时也为了理解和掌握单纯形法的基本思路，下面通过一个例题进行详细的说明和解释。

例2.4　某工厂在计划期内要安排生产甲、乙两种产品，生产单位产品所需的设备台时、A和B两种原材料的消耗以及可用资源量分别如表2.3所示。该工厂每生产一件甲产品获利2元，每生产一件乙产品获利3元，那么应该如何安排生产才使该工厂获利最多？

表2.3

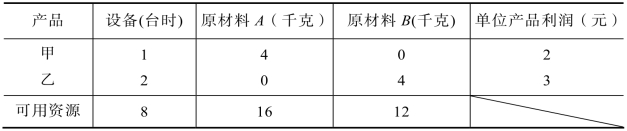
设x1、x2分别表示甲、乙两种产品的产量，则建立的线性规划模型如下：

下面对该模型用单纯形法求解：

1.寻找初始基本可行解X(0)

首先把模型（2.13）转化为标准型：

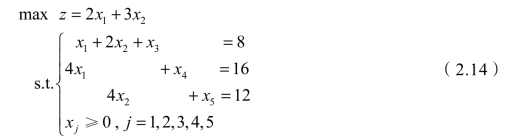
上述模型中有三个约束条件方程，基本可行解应该有三个基变量而且不违反任何约束条件，但不能任意选择三个变量作为初始基变量。假如选择x2、x4、x5作为基变量，那么x1、x3就为非基变量，即有x1=x3=0，因此根据方程组解出x2=4、x4=16、x5=-4，而x5=-4违反了非负的约束，即(x1,x2,x3,x4,x5)=(0,4,0,16,-4)不是可行解。显然，用任意估测的方式不是可行的方法，所以对于一个线性规划模型，不能任意指定m个变量作为基变量。

初始基本可行解就是迭代开始时的基本可行解。既然是基本可行解，必然和一个基本矩阵相对应，这个基本矩阵就是系数列向量组成的满秩矩阵。但判断由m个系数列向量组成的矩阵是否为满秩不是一件容易的事情，即使满秩，对应的解也不一定是可行解。

以上分析说明，必须寻找一种既简便又合理的方法来求初始基本可行解。

上例在将一般线性规划模型转化为标准型时，对“≤”约束引入了松弛变量，进而将“≤”型的约束条件方程转化为有“=”的标准型。可以看到，松弛变量对应的系数列向量是非常特殊的，即松弛变量的系数列向量都是单位列向量。这些松弛变量系数矩阵构成了单位矩阵，而单位矩阵是形式最为简单的满秩矩阵，所以完全可以作为基本矩阵。这样就可以将松弛变量作为基变量，而松弛变量以外的变量均作为非基变量。我们可令松弛变量以外的非基变量都为0，因为标准型中约束条件方程右端的值bi≥0，那么以松弛变量为基变量的值就是方程右端的常数，这样就可以直接求出松弛变量的值，从而找到了一个初始基本可行解。

在上述模型（2.14）中，x3、x4、x5是松弛变量，对应的系数列向量组成的矩阵为单位矩阵。若令非基变量x1、x2全为零，就可以解出基变量的值，即x3=8、x4=16、x5=12。此时，线性规划模型的基本可行解就是

得到初始基本可行解以后，将模型（2.14）按照表2.2的形式列出，如表2.4所示。

表2.4　初始单纯形表

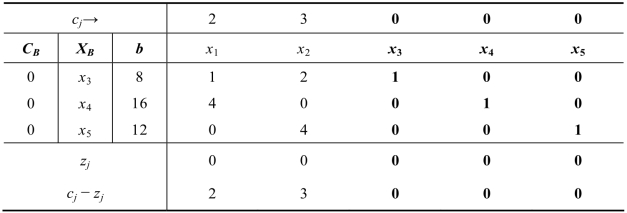
其中，机会费用zj可由公式（2.5）计算出来，如：

检验数可以直接进行计算，如c2-z2＝3-0＝3。

从当前的初始基本可行解(x1,x2,x3,x4,x5)=(0,0,8,16,12)可以看出，目标函数值z=2×0+3×0=0(元)，即实际情况是：甲、乙产品都没有生产，甲、乙产品的机会费用都为零，所以检验数cj－zj=利润-机会成本>0，它的值就是生产第j种产品可能得到的纯利润。

至此可以知道，求初始基本可行解X(0)的方法就是寻找单位矩阵，如果模型中无法找到单位矩阵，就需要设法人为地构造单位矩阵。至于如何构造单位矩阵，将在第2.3节中详细介绍。

特别提示

（1）既然通过构造单位矩阵可以获得初始基本可行解，那么单纯形法在每次计算，即每次迭代后，单纯形表中新的基变量对应的矩阵都必须为单位矩阵。

（2）当约束条件方程为“=”和“≥”这两种情况时，对于如何寻找初始基本可行解的问题，将在第2.3节的单纯形法的进一步使用中介绍。

（3）在第2.1.3节线性规划问题的标准型中，提出了为何规定bi≥0的问题，其原因是模型中要求xj≥0，而基变量的取值恰恰是约束条件方程右端常数bi的值，所以bi必须非负，即线性规划问题的标准型需要规定bi≥0。

2.判断基本可行解是否达到最优

基于第2.1.5节线性规划问题典式的分析，不妨设单纯形法在第k步迭代得到的基本可行解是X(k)，这个解对应的目标函数值为z(X(k))；再假设第k+1步迭代得到的基本可行解是X(k+1)，这个解对应的目标函数值为z(X(k+1))。可以证明，两个解所对应的目标函数值满足下面的关系式：

因为λ >0，因此若检验数cj(k)－zj(k)>0，则有

即

(www.daowen.com)

这说明新解的目标函数值比原来的解要优，否则说明新解的目标函数值没有原来的解优，算法终止。

依据以上分析，下面给出是否达到最优解的判断方法：

（1）已经达到最优解。

若所有非基变量的检验数cj－zj<0，则不管将哪一个非基变量作为换入变量，都会使

也就是已经达到最优解，计算停止。

（2）没有达到最优解。

若至少存在一个cj－zj>0，并且对应的第j列中至少存在一个aij>0，说明此时没有达到最优解，需要对当前的基本可行解进行改进，以便得到另外一个使目标函数更优的基本可行解。改进的思路就是在非基变量中选择一个，使其成为基变量，这个非基变量称为换入变量。同时，为了保证基变量的个数不变，需要从当前的基变量中选择一个，使其成为非基变量，这个基变量称为换出变量。这样就得到另外一个使目标函数更优的新的基本可行解。原则上选择检验数最大的非基变量作为换入变量，换入变量xj确定后，由下式确定换出变量：在上式中，所在的第i行所对应的基变量作为换出变量，这样确定出的新解要比原解的目标函数值优。上式确定换出变量的方法称为“最小比值原则”。其直观的经济意义就是：选择消耗资源最多的那个基变量作为换出变量，使其成为非基变量，即使其取值为0，也可以节省更多的一些资源，以使另外产品的生产数量尽可能地多，从而使追求的利润增加。

（3）无最优解。

若存在cj－zj>0，但所有cj－zj>0所在列对应的所有aij≤0，说明此时能确定换入变量但无法确定换出变量，这样就造成目标函数无上限，计算停止。

在表2.4中，存在两个cj－zj>0，即c1－z1=2、c2－z2=3，并且第1列和第2列都存在aij>0，根据上面的判断规则，此时没有达到最优，需要继续迭代寻找最优解。非基变量x2对应的检验数最大为3，并且有aij>0，所以非基变量x2作为换入变量，其取值为

其中i=3，即第3行所对应的基变量x5作为换出变量，这样，基变量就由原来的x3、x4、x5转换为x3、x4、x2，而x1、x5是非基变量，下面就需要确定新的基变量取值。

3.基本可行解的迭代计算

换入变量和换出变量确定后，需要将单纯形表的换入变量和换出变量进行置换，同时把单纯形表中CB列所在的目标函数系数做相应的变更，然后对bi和aij的值进行初等变换。变换的原则是保证新的基变量对应的矩阵调整为单位矩阵。

把表2.4中XB列的x5换为x2后，把CB列的第三行的0换为3，第三行除以4，再将新的第三行乘以-2后加到第一行，得到新的第二行。计算机会费用，如：

再计算检验数，如c5-z5＝0-3/4＝-3/4，得到新的单纯形表2.5。

表2.5

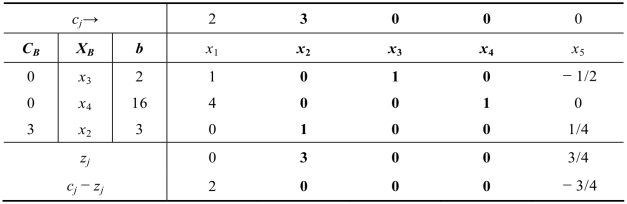
这样生成了一组新的基本可行解(x1,x2,x3,x4,x5)=(0,3,2,16,0)，得到的目标函数值为z=2×0+3×3+0×2+0×16+0×0=9(元)。表2.5中仍然有正的检验数，即c1-z1＝2，所以没有达到最优，并且存在aij>0，应继续循环迭代，得到单纯形表2.6。

表2.6

表2.6中有一组新的基本可行解(x1,x2,x3,x4,x5)=(2,3,0,8,0)，得到的目标函数值为z=2×2+3×3+0×0+0×8+0×0=13(元)。

继续进行最优判断。表 2.6 中仍然有正的检验数，即c5－z5=1/4，所以没有达到最优，并且存在aij>0，可以继续循环迭代，迭代后得到单纯形表2.7。

表2.7

在表2.7中，所有的检验数都小于等于0，所以已经达到了最优，其中最优解为(x1,x2,x3,x4,x5)=(4,2,0,0,4)，即生产4个单位甲产品和2个单位乙产品，可获得最大利润，为z=2×4+3×2+0×0+0×0+0×4=14(元)。

特别提示

下面以max型为例。在确定换入变量时，原则上选择最大检验数对应的非基变量作为换入变量。若选择其他正的检验数对应的非基变量作为换入变量，不会出现计算错误，只会造成迭代计算的过程多一些。

另外两种情况也需要仔细考虑换入变量的问题：

（1）最大的正检验数对应列不存在aij>0。

在单纯形表2.8中有两个正的检验数，非基变量x1对应的检验数最大为70，但所对应列的aij全部为负数，此时不能说无最优解。因为可以选择其他正的检验数的对应非基变量作为换入变量，如选择x3作为换入变量。

表2.8

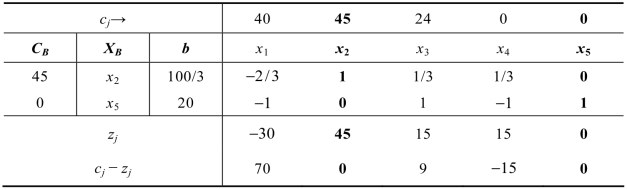
（2）所有正检验数对应的列都不存在aij>0。

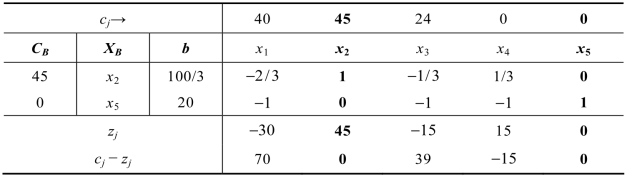
在单纯形表2.9中，有两个正的检验数，但所有正检验数对应的aij全部为负数，无法确定换出变量，所以无最优解。

表2.9