1.线性规划问题典式的生成过程

下面以线性规划问题的标准型为讨论对象：

针对线性规划模型的一组基本可行解，不妨设基变量为x1,x2,…,xm，把约束条件方程组的系数矩阵A写成分块矩阵的形式，即令A=(B,N)，其中B=(P1,P2,…,Pm)为基本矩阵，N=(Pm+1,Pm+2,…,Pn)为非基变量对应的矩阵；把目标函数系数矩阵C和未知数矩阵X也写成分块矩阵的形式，即C=(CB,CN)，X=(XB,XN)T，其中CB、XB分别为C和X中与m个基变量对应的分量组成的m维向量，CN、XN分别为C和X中与n-m个非基变量对应分量组成的n-m维向量，则约束条件方程AX=b可以写为

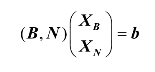
约束条件方程可写为

利用分块矩阵的乘法，把约束条件方程两边乘以-1

B，得到

移项可得到

同时，目标函数z=CX可写为

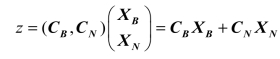
把XB=B-1b-B-1NXN代入上式可得

根据以上变换，可以把原来的线性规划模型（2.2）转化为如下等价的形式：

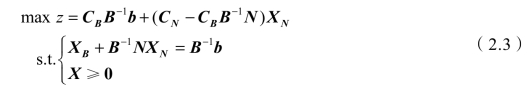
显然式（2.3）与原问题的式（2.2）是完全等价的，即两个问题的解完全相同，称式（2.3）为与可行基x1,x2,…,xm对应的线性规划问题的典式。

现在做进一步处理：

针对非基变量xj，令Pj′＝B-1Pj＝(a1′j,a2′j,…,am′j)T，令B-1b＝(b1′,b2′,…,bm′ )T，则有

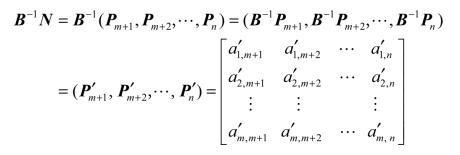
再令

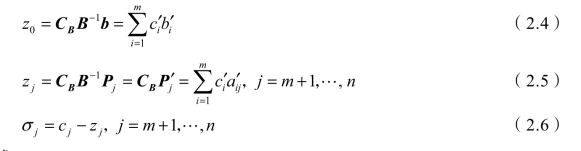
则典式（2.3）可以写成

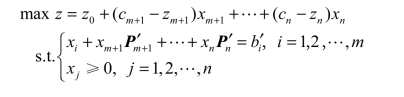
或者是

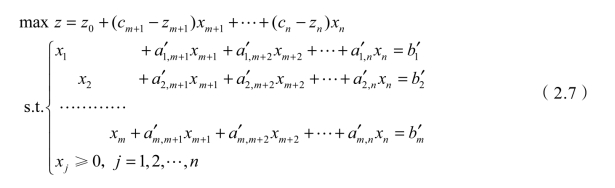
由式（2.7）可以看出，典式的基本特征是约束条件方程中基变量对应的系数列向量构成了单位矩阵。另外，每个约束条件方程中仅有一个基变量的系数不为0，称这个变量为这个约束条件方程对应的基变量。上面把最初的线性规划模型（2.2）转换为线性规划模型典式（2.7）的过程称为行运算或枢运算。

如果令非基变量xm+1,xm+2,…,xn为零，那么就很容易从典式（2.7）中直接得到基变量的值以及对应的目标值，从而可以确定一个基本解。

特别提示

式（2.3）与式（2.2）是完全等价的，同时式（2.7）与它们也是完全等价的，所以这三个等价式的解是相同的。

为了计算方便，对由任意一组基变量生成的典式，可以用表格的形式展现出来，这就是典式的表格形式。表2.2为典式（2.7）对应的表格，因为求解线性规划问题的单纯形法就是在这种表格上进行的，所以这个典式的表格也称为单纯形表。

表2.2

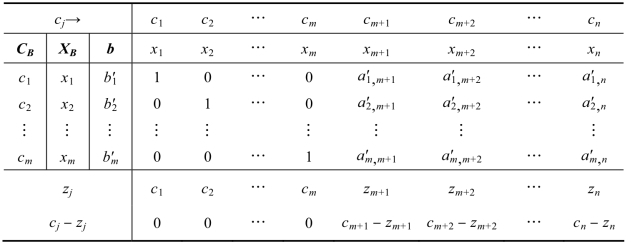
单纯形表中第一行为最初的线性规划模型（2.2）中目标函数的系数。

单纯形表中第二行为相应的符号标识。

CB所在列(第一列)为基变量在模型（2.2）中目标函数的系数。

XB所在列(第二列)为基变量对应的符号。

b所在列(第三列)为典式（2.7）中约束条件方程右端的值，也为每行基变量的取值。(www.daowen.com)

从表中第四列开始，从第三行至倒数第三行间的每一行都对应线性规划模型典式（2.7）的一个约束条件方程。

表中倒数第二行的zj称为机会费用，可以用公式（2.5）直接计算出来。

表中最后一行为典式（2.7）中目标函数的系数，称为检验数，可用公式（2.6）计算出来。

在单纯形表中，行运算是直接利用矩阵初等变换进行的，也可以把检验数的行与约束条件方程同等对待，直接进行初等变换。将检验数行中基变量对应的检验数变为0（新的基本可行解对应典式目标函数中变量的系数），那么cj－zj行中的数即为各变量对应的检验数。典式中相关系数的经济解释：取非基变量xm+k，其中k≥1，令xm+k=1，其他非基变量仍为0，由典式可直接得到

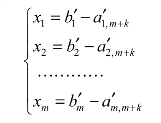
而目标函数的取值为z=z0+(cm+k－zm+k)。

可见，典式中非基变量xm+k的系数a′i,m+k为增加1个单位的xm+k以后，使得第i行的基变量xi减少的数量，检验数cm+k－zm+k则为增加一个单位的xm+k以后目标函数的变化量。从经济的角度看，为了从事第m+k项活动，一个单位需要消耗一套资源，因此需要减少当前活动的数量以获得这一套资源，而a′i,m+k就是为了获得从事第m+k项活动的一套资源而减少的第i行的基变量所对应的活动数量。第i项活动的数量xi减少a′i,m+k个单位，意味着xi对目标函数的贡献将损失cia′i,m+k。因此，为了获得从事m+k项活动一个单位所需的一套资源，目标函数将损失的数量（在经济上称为活动m+k的机会费用）为

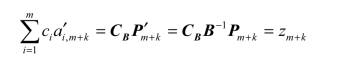
可见，式（2.5）中zj值的经济意义就是第j项活动的机会费用。另外，从事第m+k项活动一个单位对目标函数的贡献为cm+k，因此从事第m+k项活动一个单位而使得目标函数的变化量为cm+k－zm+k，这就是xm+k的检验数。

为了更好地理解上面的过程，下面以解方程组的思路予以解释。

2.举例解释

例2.3　设有下列线性规划模型：

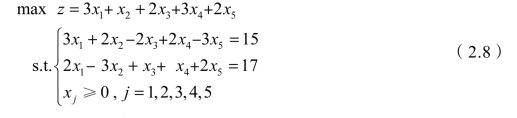
解释　先不考虑目标函数，只考虑约束条件方程组，则有如下的方程组：

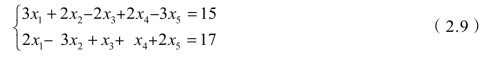
为了解等式方程组（2.9），先将第一个方程加上第二个方程乘以2，再将第二个方程乘以3减去第一个方程乘以2，得到如下的等价方程组：

在式（2.10）中，第一个方程不含x3，第二个方程不含x1，继续变换，有如下的等价方程组：

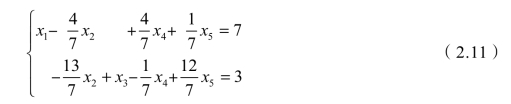
对式（2.11）继续变换，有如下的等价方程组：

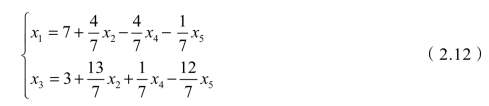
既然这些方程都是等价的，那么对式（2.12）求出的解就是式（2.9）的解。式（2.12）恰恰是函数关系，而x1、x3的取值随着x2、x4、x5的变化而变化，可以说x2、x4、x5是自变量，x1、x3是因变量，如

可见，使方程组可行的解有无数个，这些无数可行解的点集构成了可行域。显然不能用遍历的枚举法去寻找使线性规划模型（2.8）的目标函数达到最优的可行解。其实在这些无数可行解的点集中有一个特殊的解，即如果使式（2.12）中x2,x4,x5的取值为0，那么x1,x3的值就是方程右端的常数，即有

这个解对应的就是可行域的极点（顶点）。另外，由式（2.9）转换到式（2.11）的过程只是对未知数系数进行计算，所以这一过程可以用线性代数矩阵的计算方式进行。把未知数写到矩阵上方，计算过程如图2.4所示。

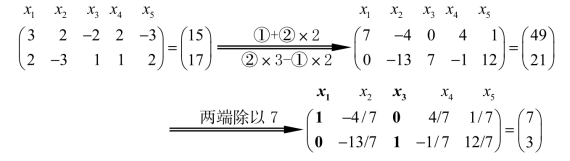
图2.4

由图2.4可看出，x1、x3的系数最后在图2.4中变为单位矩阵，这样就可以把单位矩阵对应的变量作为基变量，其余变量作为非基变量。令非基变量取值为0，则基变量的取值即为方程右端的常数，从而有基本可行解

在以上的过程中，把x1、x3作为基变量，得到了一个基本可行解，现在需要解决如何寻找另外的基本可行解，即从几何意义上来说，如何从可行域的一个极点（顶点）转到另外一个极点（顶点）上去。

为了理解其思路，需对图2.4继续进行运算，过程如图2.5所示。图2.5说明，通过构造新的单位矩阵，基变量由原来的x1、x3转换为x1、x5，从而得到另外一个新的基本可行解

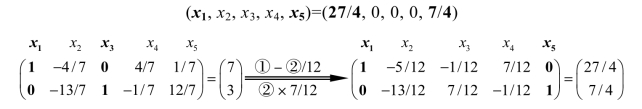
图2.5

下面的问题是，如果把式（2.8）的目标函数也考虑在内，就会面临从当前基本可行解转到哪一个基本可行解上去，才能使目标函数的值比原有的值更优一些的问题，即从几何意义上来说，从可行域的一个极点（顶点）转到另外哪一个极点（顶点）上去的问题。这个问题将在下一节的单纯形法中予以解决。

上面的过程是先从解方程组的思路，过渡到线性代数矩阵运算的思路，然后再过渡到运筹学的知识中，目的是进一步理解线性规划问题典式的生成过程，同时为下一节学习单纯形法奠定基础。

特别提示

在图2.4中，基变量为x1、x3，而在图2.5中，基变量变为x1、x5，这一变化说明，基变量的组成会随着求解过程的变化而变化。