在第2.1.1节介绍图解法时，已经直观地说明了两个变量的线性规划模型的可行域和最优解的几何意义，同时也直观地看到，若两个变量的线性规划模型存在最优解，就可以在可行域的顶点上达到。这个结论可以推广到三个或三个以上变量的线性规划模型中，从而为理论上的进一步说明和讨论奠定了基础。

以下内容主要介绍凸集的概念、相关的基本定理以及凸集的极点（顶点）与线性规划模型可行解的对应关系，主要目的是为理解线性规划模型的求解思路奠定基础。

1.基本概念

（1）凸集。

设有任意两点X(1)、X(2)在某个点集中，其中X(1)≠X(2)，如果连接这两点的线段上所有的点也在这个点集之中，则称这个点集为凸集。

凸集定义的另外一种表示形式是：设K是n维欧氏空间的一个点集，若任意两点X(1)∈K、X(2)∈K的连线上的一切点αX(1)+(1-α)X(2)∈K(0≤α≤1)，则称K为凸集。

不符合上述特征的点集称为凹集。

例如，矩形、四面体、实心圆、实心球等为凸集，即图2.3中的（a）、（b）、（c）是凸集，（d）、（e）不是凸集。

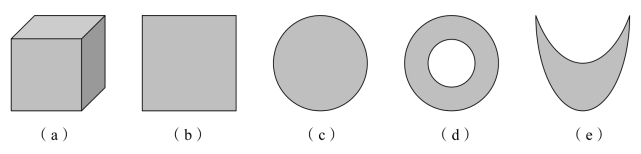
图2.3

（2）极点或顶点。

设K是一个凸集，再令X∈K，如果X不能用不同两点X(1)∈K、X(2)∈K的线性组合X＝αX(1)+(1-α)X(2)∈K(0≤α≤1)表示，则称点X是K的一个极点或顶点。其直观意义是X不是K中任何线段的内点。

（3）线性规划模型的解。

在理解第2.1.2节给出的可行解、最优解的基础上，下面基于线性规划模型的标准型，给出基本解、基本可行解以及其他概念。

可行解。满足线性规划模型（2.1）的约束条件方程组的解X=(x1,x2,…,xn)T称为线性规划问题的可行解，所有可行解的集合叫做可行域。

最优解。使线性规划模型（2.1）的目标函数达到最优的可行解叫做最优解。

基本解和基本可行解。设约束条件方程组的系数矩阵A=(aij)m×n的秩是m，其中，n为决策变量个数，m为约束条件方程的个数，n≥m。令Pj=(a1j,a2j,…,amj)T为矩阵A的第j列所对应的列向量，其中j=1,2,…,n，则AX=b可以写成

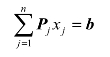
且向量组P1,P2,…,Pn的极大线性无关组包含m个向量。

不失一般性，设P1,P2,…,Pm为其极大线性无关组，则上面的方程组有唯一解(x1(0),x2(0),…,xm(0))T。令其余的变量取值为0，则得到AX=b的一个解X(0)，称此解为线性规划问题的基本解。其中，矩阵B=(P1,P2,…,Pm)称为基本解X(0)对应的基本矩阵，也简称为基矩阵。x1,x2,…,xm称为基变量，其他变量称为非基变量，基变量组成的集合称为基。若基本解X(0)同时也满足X(0)≥0，则称这个解为基本可行解。若基本可行解中非零分量的个数小于约束条件方程的个数m，则称此问题是退化的。如非特别说明，本书中讨论的问题均为非退化的。

2.基本定理

定理2.1　约束条件AX=b，X≥0的线性规划问题的可行解集合是凸集。(www.daowen.com)

证明　根据凸集定义，只要证明对任意两点X1、X2∈D都有

即可，其中0≤α≤1。

因为X1、X2∈D，则AX1=b，X1≥0和AX2=b，X2≥0，从而也有

这说明X=αX1+(1-α)X2满足条件A(αX1+(1-α)X2)=b。

又因为0≤α≤1，1-α≥0，X1≥0，X2≥0，从而有

即X满足条件αX1+(1-α)X2≥0。

由此，以上定理得证。

定理2.2　线性规划问题的可行解X是基本可行解的充要条件是X的非零分量所对应的系数列向量线性无关。

证明　必要性由基本可行解的定义即可证明。

现在证明充分性。不妨假设可行解X的前k个分量不为0，则X=(x1,x2,…,xk,0,…,0)T，P1,P2,…,Pk为X的非零分量所对应的系数列向量，因为矩阵A的秩为m，若向量P1,P2,…,Pk线性无关，则必有k≤m。当k=m时，P1,P2,…,Pk恰好构成一个基本矩阵，从而X=(x1,x2,…,xk,0,…,0)T就是对应的基本可行解；当k＜m时，则一定可从其余列向量中取出m-k个向量与P1,P2,…,Pk一起构成A的一个极大线性无关向量组，其对应的解恰为X，根据定义可知X为基本可行解。

定理2.3　线性规划问题的基本可行解X对应于可行域D的极点。

定理 2.4　线性规划问题若有可行解必有基本可行解。换句话说，线性规划问题的可行域D如为非空凸集，则必有极点。

定理2.5　线性规划问题若有最优解，则一定可以在可行域D的极点上达到。

有了定理2.5，求线性规划问题的最优解就可以不必在无穷多的可行解中搜索，只需要在有限个基本可行解中搜索即可。因为基本可行解最多有Cmn个，这样只要把有限个基本可行解依次检验有限次后就会得到最优解。

虽然基本可行解至多有Cmn个，但是当n、m较大时，Cmn仍然是一个很大的数字，计算量也同样很大。如当n=5，m=2时，基本矩阵的个数可能为10个。所谓可能为，就说明还有一些不是，所以要一个一个地判断，因此对比较大的线性规划问题，用全枚举法将所有的基本可行解都搜索出来，再计算目标函数值来选取最优解，其计算量也是很大甚至是行不通的。

著名的单纯形法用迭代法而不用全枚举法很好地解决了这个问题，其基本思路是：把当前的基本可行解调整到使目标函数值更优一点的基本可行解上去，这样仅仅检验能使目标函数值不断改进的基本可行解即可，没必要对不使目标函数值改进的基本可行解进行检验，大大减少了检验的搜索量，从而改进了计算过程。

特别提示

定理2.5并不是说只有极点才能使目标函数值达到最优而其他点不能，如多重解就是有可能在可行域内部存在使目标函数值达到最优的可行解。也就是说，如果有不是极点的其他点使目标函数值达到最优，那么一定可以找到使目标函数值达到最优的极点。