所谓图解法，就是针对不超过三个变量的线性规划问题，可以在二维或三维坐标系中，把线性规划问题画成平面图或立体图，从而对线性规划问题进行求解。这种方法简单直观，但没有过多的实用价值。这里介绍图解法的目的主要是帮助理解线性规划问题求解的基本原理。

下面通过一个例题的求解来讲述图解法的基本过程。

例2.1　用图解法求解下列线性规划模型：

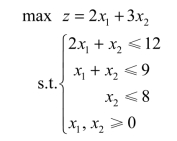
解　如图2.1所示，建立以x1和x2为坐标轴的坐标系，并在坐标系中画出所有约束条件方程所对应的等式方程的直线。在坐标系中，这些直线和区域x1、x2≥0围成了一个公共区域，在这个公共区域中的每一个点（包括边界上的点）都满足所有的约束条件方程，即每一个点对应的坐标值都是约束条件方程组的一个公共解。这个公共区域是使约束条件方程组可以行得通的域，简称为可行域。也可以这样描述，满足线性规划问题所有约束条件的一切点的集合称为可行域。

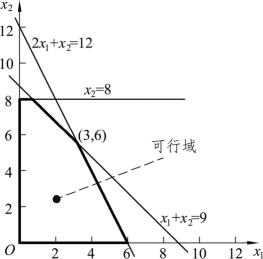
图2.1 (www.daowen.com)

那么现在的问题就是，可行域中哪个或哪些点能使目标函数z的值达到最大？

可以将目标函数z=2x1+3x2的z看成一个参数，当z取不同的值时，就形成一组不同的平行直线，如图2.2所示，其中任意一条直线上所有点具有相同的目标函数值，因而称它为目标函数z的等值线。将这些等值线向图的右上方移动时（沿着法线方向，法线是与等值线垂直的射线），z的值也随之增大，这样移动的目的是既要使目标函数z的值达到最大，又要使目标函数z的等值线上至少要有一个点位于可行域的内部或边界上。从图2.2可以看出，等值线至少有一个点既要在可行域内，又要使目标函数z值达到最大，此时等值线会停留在可行域的顶点上，这一点是(1，8)，即直线x2=8和直线x1+x2=9的相交点坐标，那么x1=1，x2=8就是这个线性规划模型最优的解，。

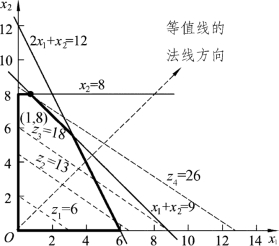
图2.2

特别提示

使目标函数达到最优的等值线恰恰停留在可行域的顶点上，这个现象正是后面对线性规划模型求解的思路。在后面的章节中，将证明使线性规划模型达到最优的解可以在可行域的顶点上找到，这样，就没有必要研究等值线，只需找出可行域的顶点并计算出每一个顶点对应的目标函数值，就可以找出使目标函数达到最优的解。