针对复杂的实际问题,构建数学模型时,要先利用理论知识、专业背景知识等对问题进行系统深入的分析,再对实际问题进行抽象、简化、假设等处理,最后明确决策变量、目标函数和约束条件方程,从而形成初步的线性规划问题。然后在此基础上,论证模型是否反映实际问题的应用、结果是否符合要求,否则要对问题重新进行分析和验证,对模型进行修改完善,这样不断反复,直到建立的模型符合实际要求为止。
在第1.1节中,例1.1和例1.2的线性规划问题相对比较简单,其原因之一就是决策变量是单变量单下标形式,即决策变量是xi形式。但有的线性规划问题的决策变量,需要设定成其他形式才能构建出合理的线性规划模型。也就是说,决策变量的设定形式多种多样,即决策变量可能用到单变量多下标,如xij形式;决策变量可能用到多变量单下标形式,如xi和yj形式;决策变量可能用到多变量多下标形式,如xi和yij形式;等等。
教材中不可能对实际工作中的大型问题进行讨论,因此下面通过几个不同类型的被简化的例题,来体会确定合适的决策变量在建立线性规划数学模型时的重要性。另外,也可以对建立线性规划模型的基本思路和技巧有进一步的了解。
下面两个例题是决策变量为单变量双下标的形式。
例1.3 某水泥厂生产R、P、L三种不同强度等级的水泥,这三种水泥是由A、B、C三种原料按照不同比例混合而成。
混合比例如下:
水泥R:A不少于10%且不多于30%;
水泥P:A不少于40%,B不少于20%且不多于30%,C不多于10%;
水泥L:B不少于20%。
三种不同强度等级的水泥R、P、L售价分别为d元/千克、e元/千克、f元/千克,另外,水泥L每月最多能销售50千克。
A、B、C三种原料的单位成本及每月的最大购入量如表1.2所示。
表1.2
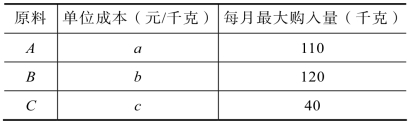
要求建立线性规划模型,确定获取最大利润的每种水泥的生产数量。
解 建立数学模型的第一步是确定决策变量。如果按照通常设x1、x2、x3分别为三种水泥的生产数量,那么就必须确切地知道相应的成本和售价,从而确定目标函数的系数cj。现在题目中已经给出了售价,但由于各种水泥的确切配方不知道,这样就不能算出各种水泥的单位成本,因此用上面定义的决策变量就不能建立该问题的线性规划模型。
针对此问题,必须作出两个决策,即每种水泥各用多少A、B、C三种原料以及每种水泥各生产多少,遇到这种情况,决策变量可采用单变量双下标的形式,这样就能顺利地构建模型。
设xij表示第j种水泥中所用原料i的数量,其中i=A,B,C;j=R,P,L。这样第j种水泥的生产量为
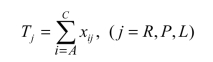
例如,水泥R的生产量为TR=xAR+xBR+xCR。
同理,原料i的需求量是:
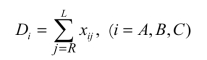
例如,原料A的需求量为DA=xAR+xAP+xAL。
目标函数就是销售总收入减去总成本的余额后,其值达到最大,即有
max z=dTR+eTP+fTL-aDA-bDB-cDC?
将水泥生产量和原料需求量的公式代入目标函数,得
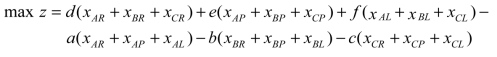
根据各种原料每月的最大购入量,可以列出如下约束条件方程:
xAR+xAP+xAL≤110
xBR+xBP+xBL≤120
xCR+xCP+xCL≤40
根据水泥L销售量的限制,可以列出如下约束条件方程:
![]()
根据水泥混合比例的限制,可以列出如下约束条件方程:

即有
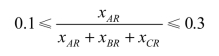
整理为
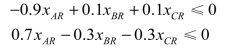
针对水泥P、L,同理可依次整理出以下方程:
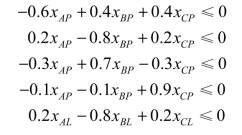
针对决策变量有非负约束,即
![]()
该问题的线性规划模型为
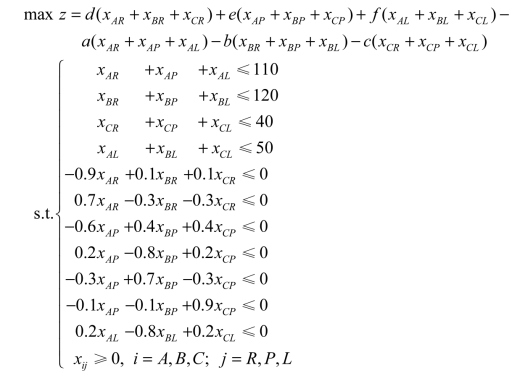
例1.4 某投资公司考虑在今后五年内投资项目。已知项目A在五年内每年均可投资,若在年初投资,两年后可收回本利120%;项目B只在第三年年初投资,到第五年年末能收回本利130%;项目C只在第二年年初投资,到第五年年末能收回本利140%;项目D在五年内每年年初可购买公债,在当年年末可收回本利106%。该部门现有资金1000万元,请建立线性规划模型来确定如何投资,使第五年年末的资金总额达到最大?
解 这是一个与时间有关的多阶段投资问题,在这里用线性规划方法静态地处理此问题,分析过程如下:
(1)确定决策变量。
设xij表示第i年年初分配给项目j的投资额,其中i=1,2,3,4,5;j=A,B,C,D。根据给定的条件可知,这些变量之间存在着一定的关系,为了利于模型的建立,将这些变量之间的关系归纳到表1.3中。
表1.3
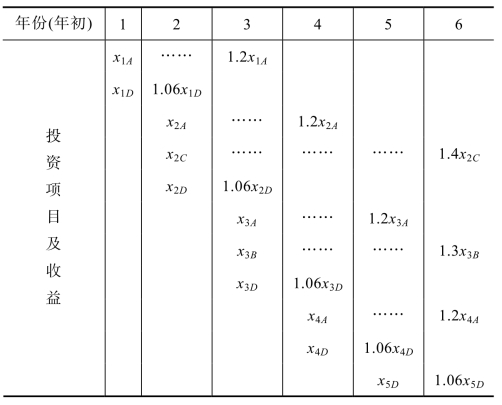
(2)目标函数。(www.daowen.com)
目标是要使第五年年末,即第六年年初拥有的资金总额达到最大,所以目标函数如下:
max z=1.4x2C+1.3x3B+1.2x4A+1.06x5D
(3)确定约束条件方程。
每年年初的投资额应等于当年年初手中拥有的资金额。另外,项目D每年都可投资,而且当年年末即可收回本利,最终该部门每年都应把资金全部投资出去,所以根据每年年初的资金平衡,可得如下约束条件方程:
第一年年初:x1A+x1D=10000000
第二年年初:x2A+x2C+x2D=1.06x1D
第三年年初:x3A+x3B+x3D=1.2x1A+1.06 x2D
第四年年初:x4A+x4D=1.2x2A+1.06x3D
第五年年初:x5D=1.2x3A+1.06x4D
基于以上分析,此问题的线性规划模型如下:
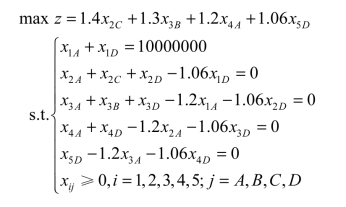
下面的例题是决策变量为双变量单下标的形式。
例1.5 某公司将在今后一个月四周内出售某种新产品,合同销售量、各周生产能力、生产成本及商品存储费见表1.4。
表1.4
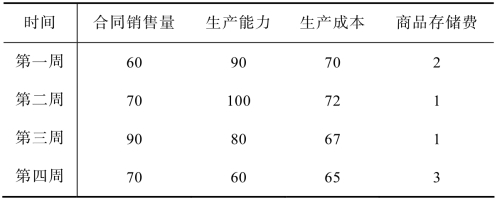
商品若在本周出售,不产生存储费,若转到下周,就要支出存储费。要求产品单位售价在今后一个月内不变,销售合同必须遵守,建立使这月利润最大的线性规划模型。
解 设xi表示第i周产品的生产量,其中i=1,2,3,4;yj表示第j周周末产品的存储量,其中j=1,2,3,4。
问题的目标是月利润最大,但是单位售价不变,所以需要转换为求成本最小,那么目标函数即为
![]()
生产能力限制的约束条件方程分别为
![]()
满足需求的约束条件方程分别为
![]()
非负约束条件为
![]()
基于以上分析,此问题的线性规划模型如下:
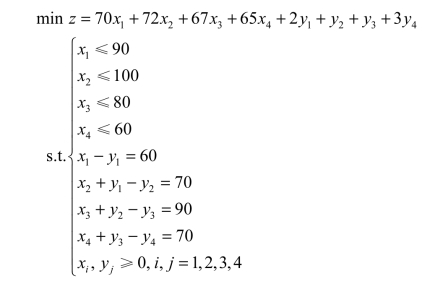
下面的例题是决策变量为双变量双下标的形式。
例1.6 有A、B、C三个零件产地,其零件要在工厂加工成成品,然后再到销售地出售。A、B两地也是销售地,其有关数据见表1.5。已知3个零件制成1个成品,A和B之间距离为150 km,B和C之间距离为200 km,C和A之间距离为100 km。每万个零件的运费为300元/km,每万个成品的运费为250元/km。如果在B地设厂,每年生产成品不能超过10万个;如果在A、C两地设厂,生产规模不受限制。试建立线性规划模型,在总费用最小的目标下,使决策人能够决定在哪几个地点设厂,生产能力又为多大?
表1.5
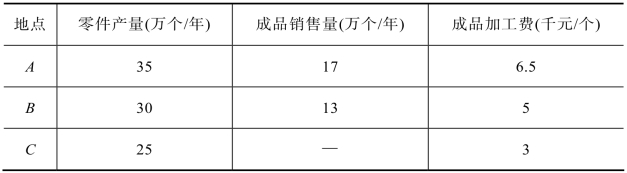
解 从表1.5可知,每年零件产量90万个,恰好是每年成品销售量30万个的3倍,用两个双下标决策变量会使模型的建立容易一些,所以设:
xij表示每年由产地i运往建厂地j的零件数量(万个),其中i=A、B、C;j=A、B、C;i≠j。
yjk表示每年由建厂地j运到销售地k的成品数量(万个),其中j=A、B、C;k=A、B。
目标为总费用最小,则有目标函数:
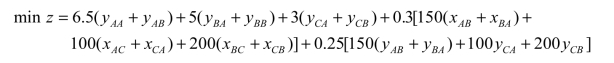
针对约束条件方程组有如下分析:
各地的零件数量应该为本地生产加上外地运来的零件,再减去运往外地的零件数量,其应该等于成品数量的3倍,则有约束条件方程:
![]()
式中出现了xBA,又出现了xAB,看起来是矛盾的,但在决策时预先不知道哪一个方向是有利的方向,因此要把这两种可能都考虑进去。由于目标函数是求生产成本最小,因此不可能产生对流运输的现象。
同理还有如下约束条件方程:
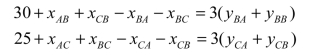
各工厂运到销售地A、B的成品数量应满足销售地A、B的销售量,则有约束条件方程:
![]()
如果在B地设厂,每年的生产规模受限制,则有约束条件方程:最后有非负约束:
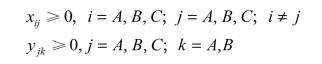
![]()
则此问题的线性规划模型为
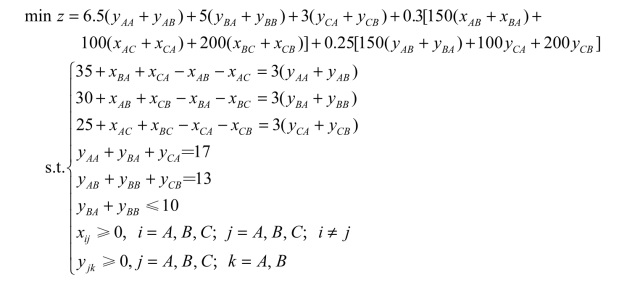
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







