基于线性规划的两个研究目的，下面引入两个例子，以便对线性规划问题以及如何建立线性规划模型有初步的了解和认识。

1.线性规划问题的提出

下面是利用有限的资源如何获取价值最高的线性规划问题示例。

例1.1　某企业生产甲和乙两种产品，甲、乙两种产品需要在车间A和车间B加工，相关资料如表1.1所示。那么该企业如何组织生产，才能使甲、乙两种产品获得的总利润最大？

表1.1

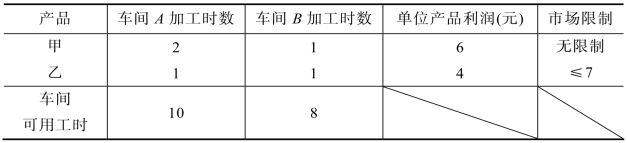
为了解决上面的问题，首先需要利用给出的资料对问题进行分析，并在深入分析的基础上，用数学语言的形式将问题刻画和描述出来（把实际问题用数学语言的形式描述出来就是建立数学模型的过程）。

问题分析　把上面的问题用逻辑图的形式进行分析，如图1.1所示。

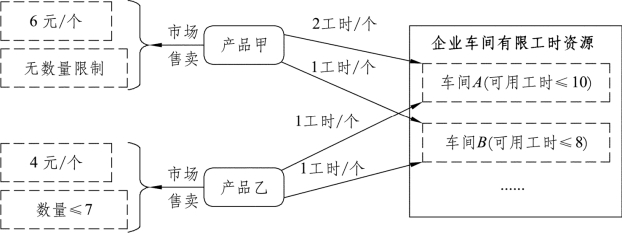
图1.1

建立数学模型

通过分析发现，甲、乙两种产品获得总利润最大取决于是否合理配置甲、乙两种产品的生产数量。在此，用未知数x1表示生产甲产品的数量，用未知数x2表示生产乙产品的数量，把设定的未知数x1、x2称为决策变量。

甲、乙两种产品获得的总利润表示为6x1+4x2，可以用数学表达式表示为

z=6x1+4x2

为了表示获得的总利润最大，用maximize的缩写max来标识，即把上面的代数式写为

max z=6x1+4x2

的形式。由高等数学函数的定义可知，此式显然是一种函数式，x1、x2是自变量，z是因变量，即此式是追求目标z值最大的关于x1、x2的函数。我们把这个函数称为目标函数。

现在从企业内部资源，即车间可用工时的角度考虑：

针对车间A，因为生产单位甲产品需要占用车间A的工时为2小时，那么生产x1个甲产品占用车间A的工时就为2x1小时；生产单位乙产品需要占用车间A的工时为1小时，那么生产x2个乙产品占用车间A的工时就为x2小时。车间A的可用工时为10小时，所以生产x1个甲产品、x2个乙产品占用车间A的总工时就不能超过10小时，即有

2x1+x2≤10

针对车间B进行同样的分析，可有代数式

x1+x2≤8

现在从企业外部，即市场限制的角度考虑：

市场对甲产品无数量限制，而市场对乙产品的数量限制是不能多于7个，即有代数式

x2≤7

另外，产品的产量不能为负数，也不能为小数，因此x1、x2必须是大于等于0的整数，即有x1,x2≥0且为整数。

以上由问题的约束条件产生的方程，称为约束条件方程。将约束条件方程合在一起称为约束条件方程组，用subject to的缩写s.t.来表示此方程组。

将上面所有的代数式合在一起，就是该问题的数学模型：

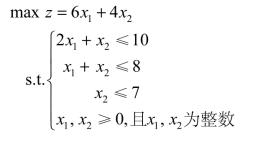
上例基于车间的有限工时资源以及市场对甲、乙产品数量的限制，对甲、乙两种产品的生产数量进行了合理确定，以获取最大利润。

下面是追求一定的目标如何使付出代价最少的线性规划问题示例。

例1.2　某公司要生产2000千克由两种原材料A、B构成的混合物，已知原材料的购买价格分别是：原材料A为6元/千克、原材料B为5元/千克，要求生产出的混合物必须满足以下规定：

（1）混合物中包含原材料A至少25%。

（2）混合物中包含原材料A不能多于65%。(www.daowen.com)

（3）混合物中包含原材料B至少30%。

现在需要设计使成本最低的混合物配制方案。

问题分析　把上面的问题用逻辑图的形式进行分析，如图1.2所示。

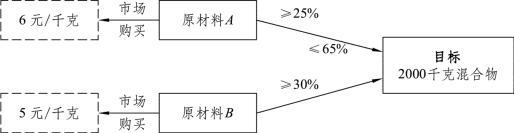
图1.2

建立数学模型

显然，配置2000千克的混合物而又使成本最低的方案，取决于原材料A和原材料B的合理购买数量，所以设定决策变量x1、x2，其中x1表示购买原材料A的数量，x2表示购买原材料B的数量。由此可知，购买原材料A、原材料B的总成本为6x1+5x2，用代数式表示为

z=6x1+5x2

为了表示总成本最低，用minimum的缩写min来标识，即把目标函数写为

min z=6x1+5x2

从配置混合物2000千克的角度考虑：

有约束条件方程：x1+x2=2000。

从原材料A在混合物中所占比例的角度考虑：

原材料A的含量不少于25%，有约束条件方程：x1/2000≥25%；

原材料A的含量不大于65%，有约束条件方程：x1/2000≤65%

从原材料B在混合物中所占比例的角度考虑：

原材料B的含量至少为30%，有约束条件方程：x2/2000≥30%。

另外，原材料A、B的数量不能为负数，因此x1、x2必须是大于等于0的数。

将上面所有代数式合在一起，就是该问题的数学模型：

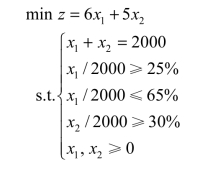
上例是追求配置2000千克混合物的目标，通过购买原材料A、原材料B的合理数量，使付出的成本最少。

2.建立线性规划模型的步骤

通过前面两个简单的例题，对线性规划问题有了初步的认识，同时也对线性规划问题模型的建立步骤有了基本的了解。

在构建线性规划问题的模型之前，首先要利用给出的资料以及相关的信息，对问题进行分析。详细、系统、深入的分析过程是构建合理、可靠、正确模型的前提，当然对问题的分析是一个较为复杂的过程，需要问题的相关背景知识和理论知识。通过对问题深入的系统分析，再利用数学方法以及一定的技能、技巧等，即可构建出能反映实际问题而且繁简适当、合理可靠的数学模型。这一过程说起来简单，真正做到并不是轻而易举的事情，所以有人说，建立数学模型与其说是科学不如说是艺术，这是有一定道理的。当然，建立模型的好与坏、优与劣也是个人建模能力的体现。

前面提到，把实际问题用数学语言的形式描述出来就是建立数学模型的过程，前面两个例题就是用数学函数、等式或不等式的形式把实际问题抽象成数学的描述。

通过例题的建模过程，基本可以看出建立线性规划问题数学模型的一般步骤。其一般步骤如下：

第一步：确定决策变量。

用设定的未知数来表示线性规划问题中未知的量，把这个设定的未知数称为决策变量。确定合理的决策变量是成功建立数学模型的关键。

第二步：确定目标函数。

线性规划问题都有特定的追求目标，把所要追求的目标用函数的形式描述出来，这个函数称为目标函数。由高等数学函数的定义可知，这个函数是以决策变量为自变量的函数。

第三步：确定约束条件方程组。

给出的问题有若干个约束条件，把这些约束条件列成代数方程式，相应的代数方程式称为约束条件方程。这些约束条件方程组成的方程组称为约束条件方程组。另外，还要注意决策变量自身取值的约束。