现在考虑Abel方程

x′=a₁（t）x+a₂（t）x²+a₃（t）x³≜P（t，x）， （7.6.1）

其中a_i（t）（i=1，2，3，t∈R）是连续可微的函数.

由定理7.1.1知，若函数Δ（t，x）是偏微分方程

的解，则扰动微分方程

x′=P（t，x）+α（t）Δ（t，x） （7.6.3）

与方程（7.6.1）是等价的.其中α（t）是任意连续的奇函数.

我们知道，要想研究微分方程（7.6.3）的解的性质比研究Abel方程（7.6.1）要困难得多.有关Abel方程解的性质的研究已取得了若干好的结果见参考文献[47-49]等.现在我们应用反射函数来讨论Abel方程（7.6.1）解的性态，以及讨论与其等价的微分方程族解的性态.

定理7.6.1 假设

其中

则F（t，x）=f₀+f₁x为（7.6.1）的反射函数.并且，当a_i（t）（i=1，2，3）为2ω-周期时，Abel方程（7.6.1）的所有解是2ω-周期解.

此结论可以通过验证F（t，x）=f₀+f₁x满足关系式（2.1.5）和式（2.1.6）以及F（-ω，x）≡x来证明.

例7.6.1 Abel方程

的反射函数为F（t，x）=e^sintx，其中γ₁（t），γ₂（t）为任意连续可微的奇函数.当该方程为2π-周期方程时，该方程所有的解都是2π-周期的.

定理7.6.2 Abel方程

x′=a₁（t）x+a₃x³ （7.6.4）

的反射函数为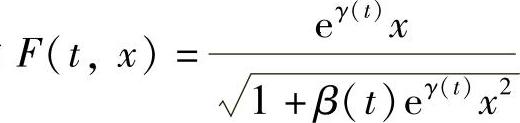，其中，

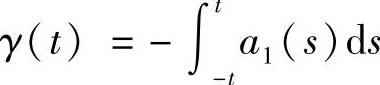若a₁（t），a₂（t）为2ω-周期函数，当β²（-ω）+γ²（-ω）=0时，该Abel方程所有的解都是2ω-周期解；当（e^γ（-ω）-e^-γ（-ω））β^（-ω）＞0时，方程（7.6.4）有三个2ω-周期解.当（e^r（-ω）-e^-r（-ω））β（-ω）＜0时，除零解以外，该Abel方程不存在2ω-周期解.

定理7.6.3 若函数b_i（t），i=0，1，2，3满足以下关系

则方程（7.6.3）等价于Abel方程（7.6.1），其中

Δ（t，x）=b₀（t）+b₁（t）x+b₂（t）x²+b₃（t）x³，b_i（t）（i=0，1，2，3）为连续可微的函数.

证 将Δ（t，x）=b₀（t）+b₁（t）x+b₂（t）x²+b₃（t）x³，代入关系式（7.6.2）且比较等式两边x的同次幂系数，可得关系式（7.6.5）.即结论得证.

类似地，我们可得

定理7.6.4 令（b_0i（t），b_1i（t），b_2i（t），b_3i（t））（i=1，2，…，m）满足关系式（7.6.5），β_it（t）为奇函数.则下列形式的方程

（7.6.6）

等价于Abel方程（7.6.1）.

例7.6.2 Abel方程.

等价于

容易验证函数F（t，x）=e^sintx是方程（7.6.7）的反射函数.因此方程（7.6.7）的Poincaré映射为T（x）=F（-π，x）≡x.由此可知方程（7.6.7）的所有解都是2π-周期解.因此，当α（t）为2π周期连续可微的奇函数时，方程（7.6.8）的所有解都是2π-周期解.

下面记

这里c₀·c₂≠0，且c_i∶=c_i（t），b_j∶=b_j（t）（i=0，1，2，j=0，1，…5）为连续可微的函数.(www.daowen.com)

其中

d₁=a₁c₀， d₂=a₁c₁+a₂c₀， d₃=a₁c₂+a₂c₁+a₃c₀，

d₄=a₂c₂+a₃c₁， d₅=a₃c2.

定理7.6.5

（i）若关系式（7.6.10）～式（7.6.17）成立，则Abel方程（7.6.1）等价于方程（7.6.3），其中函数Δ（t，x）由式（7.6.9）表示.

（ii）若关系式（7.6.10）～式（7.6.17）成立，且W≠0，则Abel方程（7.6.1）等价于方程（7.6.3），且方程（7.6.3）也是Abel方程.

（iii）若关系式（7.6.10）～式（7.6.17）成立，且δ²₁（0）+δ²₂（0）=0，则Abel方程（7.6.1）等价于方程（7.6.3），且方程（7.6.3）也是Abel方程.

证 将式（7.6.9）代入关系式（7.6.4）且比较等式两边x的同次幂系数，可得

b₀′c₀^-c0′b₀=b₀d₁， （7.6.18）

b₀′c₁+b₁′c₀-b₀c₁′-b₁c₀′=2b₀d₂， （7.6.19）

b₀′c₂+b₁′c₁+b₂′c₀-b₀c₂′-b₁c₁′-b₂c₀′=-b₂d₁+b₁d₂+3b₀d₃， （7.6.20）

b₁′c₂+b₂′c₁+b₃′c₀-b₁c₂′-b₂c₁′-b₃c₀′=-2b₃d₁+2b₁d₃+4b₀d₄， （7.6.21）

b₂′c₂+b₃′c₁+b₄′c₀-b₂c₂′-b₃c₁′-b₄c₀′=-3b₄d₁-b₃d₂+b₂d₃+3b₁d₄+5b₀d₅，

（7.6.22）

b₃′c₂+b₄′c₁+b₅′c₀-b₃c₂′-b₄c₁′-b₅c₀′=-4b₅d₁-2b₄d₂+2b₂d₄+4b₁d₅，

（7.6.23）

b₄′c₂+b₅′c₁-c₁′b₅-b₄c₂′=-3b₅d₂-b₄d₃+b₃d₄+2b₂d₅， （7.6.24）

b₅′c₂-c₂′b₅=-2b₅d₃+2b₃d₅， （7.6.25）

b₅d₄=b₄d₅. （7.6.26）

由式（7.6.18）～式（7.6.20）及式（7.6.23）～式（7.6.25），可得式（7.6.12）～式（7.6.14）及式（7.6.15）～式（7.6.17），将它们代入式（7.6.21）及式（7.6.22）可得

因为等式（7.6.15）与式（7.6.27）等价，等式（7.6.16）与式（7.6.28）等价，应用式（7.6.26），可得式（7.6.10）～式（7.6.11）成立.因此，当关系式（7.6.10）～式（7.6.17）成立时，等式（7.6.4）也成立.因此，方程（7.6.1）和方程（7.6.3）等价.

当W≠0时，方程（7.6.10）～方程（7.6.11）有且仅有零解，即δ₁（t）=δ₂（t）=0，因此

其中，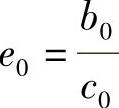

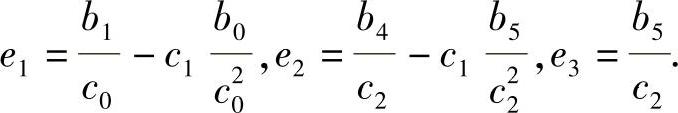
此时，方程（7.6.3）也是Abel方程.

应用关系式（7.6.12）～式（7.6.17），可得

由定理的假设知，以上线性系统满足初值δ₁（0）=0，δ₂（0）=0的解唯一，即δ₁（t）=0，δ₂（t）=0，此时Δ（t，x）由式（7.6.29）表示，从而方程（7.6.3）为Abel方程.

推论7.6.1 如果

满足定理7.6.5的条件，则Abel方程（7.6.1）等价于方程

x′=a₁（t）x+a₂（t）x²+a₃（t）x³+∑β_k（t）Δ_k（t，x），β_k（t）为任意连续可微的奇函数.同理可以讨论与多项式微分方程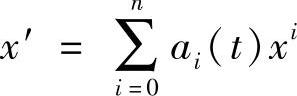等价的方程类及其解的性态.