线性系统等价性的应用-微分系统的反射函数理论及其应用

在这一节里我们将讨论与线性系统等价的微分系统族.

考虑线性系统

x′=A（t）x， t∈R， x∈Rⁿ， （7.4.1）

这里A（t）是一个关于t的连续矩阵函数.

记u（t，x）=（u₁（t，x），u₂（t，x），…，u_n（t，x）），这里u_i（t，x）=c_i是系统（7.4.1）的独立的首次积分，c_i（i=1，2，…，n）是常数，Φ（t）是系统（7.4.1）的一个基解矩阵.

引理7.4.1 假设Δ（t，x）=Φ（t）S（u（t，x）），这里S（u）是一个任意的连续可微的向量函数，则它满足关系式

Δ_t′+Δ_x′A（t）x-A（t）Δ=0. （7.4.2）

证 由于u_t′+u_x′A（t）x=0，Φ′（t）=A（t）Φ（t），则

Δ_t′+Δ_x′A（t）x-A（t）Δ

=Φ′（t）S（u）+Φ（t）S′（u）u_t′+Φ（t）S′（u）u_x′A（t）x-A（t）Φ（t）S（u）≡0.

定理7.4.1 假设α_k（t）是任意奇的连续纯量函数，且Δ_k=Φ（t）S_k（u），Sk（u）（k=1，2，…，m）是任意连续可微的向量函数，则微分系统

等价于微分系统（7.4.1）.

此外，若微分系统（7.4.1）和系统（7.4.3）是2ω-周期系统，则系统（7.4.3）定义在[-ω，ω]上的解x（t）是2ω-周期函数，当且仅当，y（t）（y（-ω）=x（-ω））为微分系统（7.4.1）的2ω-周期解.

证 由引理7.4.1知，Δ_k（k=1，2，…，m）是方程（7.4.2）的解.又由定理7.1.1知，微分系统（7.4.3）和系统（7.4.1）等价，故它们的Poincaré映射相同.从而定理的结论正确.

类似地，我们可以得到下面的结果

推论7.4.1 若Δ_k=Φ（t）D_k（u）Φ^-1（t）x，这里D_k（u）是一个任意连续可微的矩阵函数，则微分系统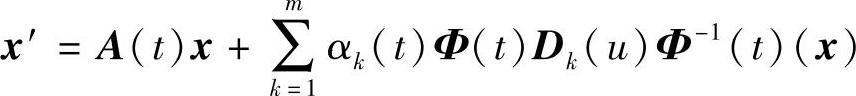与微分系统（7.4.1）等价.

推论7.4.2 微分系统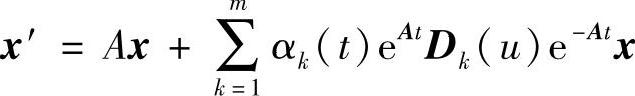与常系数微分系统x′=Ax等价，这里A是一个常数矩阵.

推论7.4.3 若α_k（t）是任意纯量连续奇函数，且Δ_k=S_k（u）X（x），S_k（u） （k=1，2，…，m）

是任意的连续可微纯量函数，则微分系统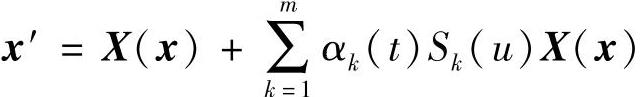与自

治微分系统x′=X（x）等价，其中

u（t，x）=（u₁（t，x），u₂（t，x），…，u_n（t，x）），u_i（t，x）=c_i（i=1，2，…，n）是系统x′=X（x）的独立首次积分.

推论7.4.4 若u_i（t，x_i）=c_i（i=1，2，…，n）是方程x_i′=f_i（x_i）g_i（t）（i=1，2，…，n）的首次积分，则微分系统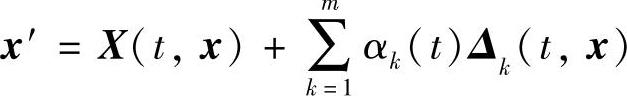与微分系统x′=X（t，x）等价，这里

Δ_k=（Δ_k1，Δ_k2，…，Δ_kn）^T，

X（t，x）=（f₁（x₁）g₁（t），f₂（x₂）g₂（t），…，f_n（x_n）g_n（t））^T，

Δ_ki=S_ki（u_i（t，x_i））f_i（x_i），

且α_k（t）为任意纯量奇函数，g_k（t），f_k（x）与S_ki（u）为任意纯量连续可微函数（i=1，2，…，n，k=1，2，…，m）.

注7.4.1 若推论7.4.1～推论7.4.4中所有等价系统都是关于t的2ω-周期系统，则它们的2ω-周期解的定性性质相同.

例7.4.1 微分系统

与微分系统

等价.这里β=1-cost，α_k（t）（k=1，2，…，m）为任意连续纯量奇函数，S₁=S₁（u₁，u₂），S₂=S₂（u₁，u₂）为任意连续可微函数，u₁=e^-sint（xcosβ-ysinβ），u₂=e^-sint（xsinβ+ycosβ）。

进一步地，若α_k（t）（k=1，2，…，m）为2π-周期奇函数，则微分系统（7.4.4）定义在[-π，π]上的所有解为2π-周期函数.这是由于微分系统（7.4.4）的反射函数为F（t，x，y）=（e^-2sintx，e^-2sinty）^T且F（-π，x，y）≡（x，y）^T.

下面我们将讨论简单系统（定义2.3.3）或最简系统（定义2.3.2）与一些线性系统之间的等价性.

在本节我们将记A∶=A（t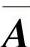），∶=A（-t），F∶=F（t），“detA（t）≠0”表示在t=0的去心邻域内，|t|足够小时detA（t）≠0.

定理7.4.2 若系统（7.4.1）是以F（t，x）为反射函数的简单系统，则系统（7.4.1）等价于系统

这里α_k（t）（k=1，2，…，m）为任意连续纯量奇函数.

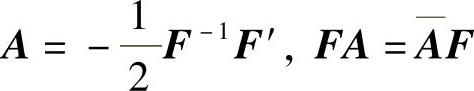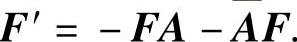证 由定理的假设得且因此

即F也是系统（7.4.5）的一个反射矩阵.

定理7.4.3 若系统（7.4.1）是以F（t，x）为反射函数的简单系统，矩阵函数D_j（j=1，2，…，l）满足关系式

则系统

等价于系统（7.4.1），这里α_k（t）（k=1，2，…，m），β_j（t）（j=1，2，…，l）为任意连续纯量奇函数.

证 要证明系统（7.4.1）与系统（7.4.6）等价，只需验证

记U=FD_j-D_jF，则U（0）=0，(https://www.daowen.com)

若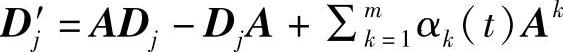，则

若D_j′=AD_j-D_jA+∑_k^m=₁α_k（t）D_j^k，则

由线性微分系统初值问题解的唯一性，可得U≡0.因此F也是系统（7.4.6）的反射矩阵.

例7.4.2 微分系统

是一个简单系统，其反射矩阵为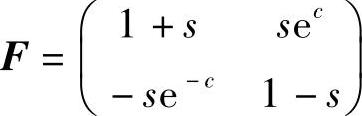，这里s=sint，c=cost.由定理7.4.2可知，该系统等价于系统

这里α_k（t）（k=1，2，…，m）为任意连续可微纯量奇函数.且当α_k（t+2π）=a_k（t）（k=1，2，3，…，m），则上面等价的两个系统定义在[-π，π]上的所有解都为2π-周期函数.

若线性系统（7.4.1）是以F（t，x）=F（t）x为反射函数的最简系统，我们也可以称该线性系统是以F（t）为反射矩阵的最简系统.

由定理2.3.2可知，若系统x′=X（t，x）是以F（t，x）为反射函数的最简系统，则X（t，x）=X（-t，F（t，x））.反过来说，若该恒等式成立且它的解F为该系统的反射函数，则该系统为最简系统.

注7.4.2 若A（t）+A（-t）=0且detA（t）≠0，则微分系统（7.4.1）不是最简系统.

定理7.4.4 若det（A）≠0且

则系统（7.4.1）是以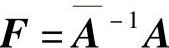为反射矩阵的最简系统.

证 由于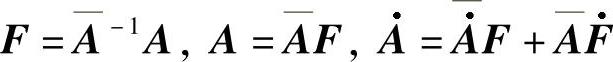，因此

即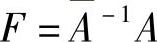是系统（7.4.1）的一个反射矩阵，则系统（7.4.1）是以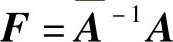为反射矩阵的最简系统.

由该定理我们很容易得到下面几个推论.

推论7.4.5 若det（A）≠0，且

则系统（7.4.1）是以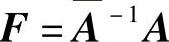为反射矩阵的最简系统，这里α_j（t）（j=1，2，…，n）为任意纯量奇函数，S_j（j=1，2，…，n）为任意可微函数.

推论7.4.6 若det（A）≠0，且

则系统（7.4.1）是以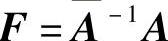

t→0为反射矩阵的最简系统，这里S（t，A）为一个任意可微矩阵函数.

推论7.4.7 若定理7.4.2的条件都满足，则系统（7.4.1）等价于系统

和

x′=Ax+A^-1（S（t，Ax）-S（-t，Ax））.

现在考虑线性系统

x′=Bx， （7.4.8）

这里B=B（t）是一个连续可微矩阵函数.

定理7.4.5 若det（A）≠0，式（7.4.7）成立且

则系统（7.4.8）等价于系统（7.4.1）.

证 由定理7.4.4可知是系统（7.4.1）的一个反射矩阵，则

即也是系统（7.4.8）的反射矩阵.推论7.4.8 若是系统（7.4.1）的反射矩阵，且

则系统（7.4.8）等价于系统（7.4.1）.推论7.4.9 若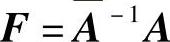是系统（7.4.1）的反射矩阵，则系统（7.4.1）等价于系统

这里α_j（t），R_j（t）（j=1，2，…，m）是使得系统（7.4.10）等式右端函数连续可微的任意函数，α_j（t）是纯量奇函数，R_j（t）（j=1，2，…，m）是n×n阶偶矩阵函数.

容易验证微分系统（7.4.10）满足推论7.4.8的所有条件.

注7.4.3 若定理7.4.5或推论7.4.8或推论7.4.9的条件成立，且系统（7.4.1），系统（7.4.7）和系统（7.4.10）为关于t的2ω-周期系统，则它们定义在[-ω，ω]上的所有解是2ω-周期解.该结论可由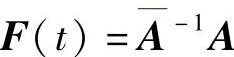和F（-ω）=E推得.

例7.4.3 微分系统

是以矩阵

为反射矩阵的最简系统.这里

a₁₁=2cost+sin³t，

a₁₂=e^cost（2cost+sin³t-2sin²t），

a₂₁=-e^-cost（2cost+sin³t+2sin²t）.

该系统等价于系统

这里α_j（t）（j=1，2，…，m）为任意连续纯量奇函数，R_j（t）（j=1，2，…，m）为连续可微的2×2阶矩阵函数.且当系统（7.4.11）是一个关于t的2π-周期系统时，系统（7.4.11）定义在[-π，π]上的所有解为2π-周期解.