在7.1中我们已介绍对于微分系统
若Δk(t,x)为偏微分方程
Δt+ΔxX-XxΔ=0 (7.3.2)
的解,则系统(7.3.1)等价于系统
本节我们将证明
与系统(7.3.3)等价,当且仅当,
其中Δk为方程(7.3.2)的解,αk(t)(k=1,2,…,m)为连续可微的奇函数.
为此首先给出几个引理.
引理7.3.1 2ω-周期系统 =X(t,x)的反射函数F(t,x)=x的充要条件为
=X(t,x)的反射函数F(t,x)=x的充要条件为
证 必要性 设F(t,x)=x为系统(7.3.3)的反射函数,则
X(t,x)+X(-t,x)=0.
又由于X(t+2ω,x)=X(t,x),则X(t,x)可展开成正弦级数,即
充分性 设
又 (Xk(x))t+Xk′(x)0-0Xk(x)≡0, sinkt+sin(-kt)=0,
则由定理7.1.1的推论可得 等价于
等价于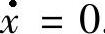 .又
.又 的反射函数为F≡x,从而结论成立.
的反射函数为F≡x,从而结论成立.
引理7.3.2 设φ(t;t0,x0)为系统(7.7.3)满足条件x(t0)=x0的解,F(t,x)为其反射函数,则F(t,x)=φ(-t;0,φ(0;t,x)).
证 设(t0,x0)为任意一点,x(t)为过该点的解,则由反射函数的性质得
F(t,x(t))≡x(-t)≡φ(-t;0,x(0))≡φ(-t;0,φ(0;t,x(t))),
则
F(t,x(t))≡φ(-t;0,φ(0;t,x(t))).
特别地
F(t0,x0)=φ(-t0;0,φ(0;t0,x0)),
则由(t0,x0)的任意性可得引理的结论成立.
引理7.3.3 设F(t,x)为系统(7.3.3)和系统(7.3.4)的反射函数,φ(t;t0,x0)为系统(7.3.3)过(t0,x0)的解,则式(7.3.4)可通过变换z=φ(0;t,y)化为
且
Z(t,z)+Z(-t,z)=0.
证 设z(t)=φ(0;t,y)为式(7.3.6)的任一解,y(t)为系统(7.3.4)的任一解,则
z(-t)≡φ(0;-t,y(-t))≡φ(0;-t,F(t,y(t)))
≡φ(0;-t,φ(-t;0,φ(0;t,y(t))))
≡φ(0;t,y(t))=z(t),
即式(7.3.6)的任一解为t的偶函数,从而式(7.3.6)的反射函数Φ(t,z)≡z,从而式(7.3.6)的右端为t的奇函数.
定理7.3.1 微分系统(7.3.3)与系统(7.3.4)具有相同的反射函数,当且仅当,系统(7.3.4)满足条件y(0)=z(0,y0)的解可表示为y=φ(t;0,z(t,y0)),其中φ(t;0,x0)为系统(7.3.3)满足条件x(0)=x0的解,z(t,y0)是一个关于y0,t具有反函数的向量函数.
证 必要性 设系统(7.3.4)的反射函数与系统(7.3.3)相同,则由引理7.3.3,通过变换z=φ(0;t,y),即y=φ(t;0,z),微分系统(7.3.4)可化为式(7.3.6),且Z(t,z)=-Z(-t,z),即系统(7.3.6)具有反射函数Φ(t,z)=z,从而,式(7.3.6)满足条件z(0)=z0的解z(t,z0)=z(-t,z0),则y=φ(t;0,z(t,y0)),(y0=z0),z(t,y0)+z(-t,y0)=0,z=φ(0;t,y)关于y可逆.即必要性成立.
充分性 假设式(7.3.4)的解可表示为y=φ(t;0,z(t,y0)),则
y(-t)=φ(-t;0,z(-t,y0))=φ(-t;0,z(t,y0))
=φ(-t;0,φ(0;t,y(t)))≡φ(-t;t,y(t))=F(t,y(t)).
由反射函数的性质可得,F(t,y)为系统(7.3.4)的反射函数.
定理7.3.2 微分系统
等价于系统(7.3.3)的充要条件为
其中Δk(t,x)为系统(7.3.2)的解,αk(t)+αk(-t)=0 (k=1,2,…,).
证 充分性由定理7.1.1及其推论可得.
下证必要性 设φ(t;0,x0)为系统(7.3.3)满足x(0)=x0的解,并设在R上有定义,由定理7.3.1,微分系统(7.3.7)的解可表示为x=φ(t;0,z(t,x0)).由条件知,系统(7.3.7)的反射函数与系统(7.3.3)的反射函数相同.又由φ(t;0,x)的定义可知,
φ(0;t,φ(t;0,x))≡x.
由此可导得
记U(t,x)∶=φ(0;t,x).由于对于式(7.3.3)的解x=φ(t;0,x0)有
φ(0;t,φ(t;0,x0))=x0=x(0).
故U(t,x)为微分系统(7.3.3)的首次积分,从而又
记 为函数z(t,x)的反函数,则由x=φ(t;0,z(t,x0))推得z(t,x0)=φ(0;t,x)≡U(t,x).
为函数z(t,x)的反函数,则由x=φ(t;0,z(t,x0))推得z(t,x0)=φ(0;t,x)≡U(t,x).
从而 (t;U(t,x)),因此
(t;U(t,x)),因此
再应用式(7.3.9)可得
由于z(t,x)为t的偶函数,则其反函数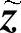 (t,x)也是t的偶函数,从而
(t,x)也是t的偶函数,从而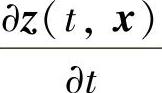 为t的奇函数,因此
为t的奇函数,因此 为t的奇函数,则
为t的奇函数,则
从而
下面验证
Δkt+ΔkxX-XxΔk=0.
事实上,由式(7.3.9)及U(t,x)为方程(7.3.3)的首次积分,可计算得
从而定理的必要性成立.
注7.3.1 由定理7.3.2,对于任意系统(7.3.3),我们可以构造一个系统(7.3.7),使得系统(7.3.7)具有形式
Δk(t,x)满足式(7.3.2),αk(t)+αk(-t)=0,k=1,2,….
如果系统(7.3.3)为自治的,此时式(7.3.2)化为
下面我们假设X(x)任意次可微向量函数,我们将寻找式(7.3.11)幂级数形式的解
Δ=a0(x)+a1(x)t+…+an(x)tn+… (7.3.12)
将此代入式(7.3.11)并比较等式两边t的同次幂的系数可得
a1(x)+a0′(x)X(x)-X′(x)a0(x)=0,
kak(x)+ak′-1(x)X(x)-X′(x)ak-1(x)=0 (k=1,2,…) (7.3.13)
由此我们可解出ak(x),k=0,1,2,…从而可得级数(7.3.12).最后再证明其收敛即可.(https://www.daowen.com)
例7.3.1 考虑方程
若我们选a0(x)≡1,则得Δ1=(1+tx)2.若选a0(x)≡x,则得Δ2=x+tx2.若选a0(x)≡x2,则得Δ3=x2.因此,所有具有形式
即方程
与 等价,这里αk(t)为任意连续可微的奇函数.下面讨论线性微分系统
等价,这里αk(t)为任意连续可微的奇函数.下面讨论线性微分系统
这里P(t)在R上连续,记Φ(t)为其基解矩阵,由7.3知,线性系统
与系统(7.3.14)具有相同反射函数的充要条件是
S(t)=F(-t)R(t)-R(-t)F(t),
这里R(t)是一个任意连续矩阵,并且
F(t)=Φ(-t)Φ-1(t)
为系统(7.3.14)的反射矩阵.
从而
S(t)=F(-t)R(t)-R(-t)F(t)
=Φ(t)Φ-1(-t)R(t)-R(-t)Φ(-t)Φ-1(t)
=Φ(t)[Φ-1(-t)R(t)Φ(t)-Φ-1(t)R(-t)Φ(-t)]Φ-1(t),
即
S(t)=Φ(t)A(t)Φ-1(t),
这里A(t)∶=Φ-1(-t)R(t)Φ(t)-Φ-1(t)R(-t)Φ(-t)是一个奇的连续矩阵函数.因此,我们可以将S(t)表示为
其中aij(t)为奇的纯量函数,Cij为常数矩阵.而且Δij(t,x)=[X(t)CijX-1(t)]x满足方程
Δt+ΔxP(t)x-P(t)Δ=0. 这就是定理7.3.2在线性情况下的结论.下面讨论两个等价系统解之间的相互关系[85].
这就是定理7.3.2在线性情况下的结论.下面讨论两个等价系统解之间的相互关系[85].
引理7.3.4 设微分系统(7.3.3)为2ω-周期的,其反射函数为F(t,x),其解为x(t),系统(7.3.4)与系统(7.3.3)等价,系统(7.3.4)的反射函数为Φ(t,x)=F(t,x),其解为y(t),若
x(-ω)=y(-ω) (7.3.15)
且x(t),y(t)可以延拓到[-ω,∞]上,则
x(2kω-ω)=y(2kω-ω),k∈N+. (7.3.16)
证 下面我们用数学归纳法来证明上述结论.
由式(7.3.15)及x(ω)=F(-ω,x(-ω))=Φ(-ω,x(-ω))=Φ(-ω,y(-ω))=y(ω)得,式(7.3.16)在k=1时成立.
假设k=n时式(7.3.16)成立.下证k=n+1时也成立,即
x(2nω+ω)=y(2nω+ω). (7.3.17)
事实上,记z(t)=x(2kω+t),则z(t)也是系统(7.3.3)的解,同样记u(t)=y(2kω+t),则它也是系统(7.3.4)的解.由于z(-ω)=x(2kω-ω)=y(2kω-ω)=u(-ω),与前同理可得z(ω)=u(ω),即式(7.3.16)成立.
由数学归纳法,引理的结论成立.
定理7.3.3 设2ω-周期系统(7.3.3)等价于自治系统
并且
(A)x(-ω)=y(-ω);
(B)系统(7.3.18)的解可以延拓到[-ω,∞];
(C)存在一个常数a使得‖y(2kω-3ω)‖≤a,k∈N+;
(D)系统(7.3.3)满足不等式‖x(-ω)‖≤a的解都在[-ω,ω]上有定义,则系统(7.3.3)的解x(t)可以延拓到[-ω,∞)上且有界.
证 首先证明x(t)可以延拓到[-ω,∞)上.由条件(A)和(C)知
‖x(-ω)‖=‖y(-ω)‖≤a,
则由(D)得x(t)在[-ω,ω]上有定义,即结论当k=1时成立.
下证x(t)可以延拓到[-ω,3ω]上,记z(t)=x(t+2ω)由于系统(7.3.3)为2ω-周期系统,则z(t)也是系统(7.3.3)的解,且
‖z(-ω)‖=‖x(ω)‖=‖y(ω)‖≤a. (由引理7.3.4)
又由条件(D)可知z(t)可以延拓到[-ω,ω]上,也就是说x(t)能延拓到[-ω,3ω]上.应用数学归纳法我们可证x(t)可以延拓到[-ω,2kω+ω]上,再由k为任意的,从而可推知x(t)可以延拓到[-ω,∞)上.
下面证明x(t)在[-ω,∞)上有界.
由于所有满足‖x(-ω)‖≤a系统(7.3.3)的解x(t)可以延拓到[-ω,ω]上,则存在一个常数m使得‖x(t)‖≤m,对任意t∈[-ω,ω]成立.又由引理7.3.4知
x(2kω-3ω)=y(2kω-3ω)
对所有的整数k都成立.因此,对于z(t)∶=x(t+2kω)有
‖z(-ω)‖=‖x(2kω-ω)‖=‖y(2kω-ω)‖≤a,
从而
‖x(t+2kω)‖=‖z(t)‖≤m, t∈[-ω,ω].
因此,由正整数k的任意性得x(t)在[-ω,∞)上有界.
定理7.3.4 假设定理7.3.3中的条件(A),(C),(D)都成立,并且微分系统(7.3.18)的解y(t)为2ω-周期的且渐近稳定(或不稳定),则系统(7.3.3)的解x(t)也是2ω-周期且渐近稳定(或不稳定).
证 设y(t)为2ω-周期解,则
x(ω)=F(-ω,x(-ω))=Φ(-ω,x(ω))=Φ(-ω,y(-ω))=y(ω)
=y(-ω)=x(-ω),
即x(ω)=x(-ω),由此推出x(-ω)为[-ω,ω]上的Poincaré映射F(-ω,x)的不动点,从而x(t)为2ω-周期解.又由于F(-ω,x)和Φ(-ω,x)是相同的Poincaré映射,从而周期解x(t)和y(t)的稳定性相同.
例7.3.2 考虑微分系统
这里a(t),b(t)为连续的2π-周期函数,且α1(t)∶=a(t)-1,α2(t)∶=b(t)-1为奇函数.
容易验证这个系统等价于自治系统
这里 Δ0=α1Δ1+α2Δ2,
Δ1=(x-x(x2+y2),y-y(x2+y2))T,
Δ2=(y,-x)T,
X=(x+y-x(x2+y2), -x+y-y(x2+y2))T,
Δ1t+Δ1xX-XxΔ1=0,
Δ2t+Δ2xX-XxΔ2=0.
由于系统(7.3.20)有一个渐近稳定的极限环x2+y2=1(即(x(t),y(t))为2π-周期解),由定理7.3.4可推得(7.3.19)的从t=-π,x2(-π)+y2(-π)=1上出发的解为2π-周期并且除零解以外的非零解都在t→+∞时逼近该周期解.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








