等价系统构造-微分系统反射函数理论及应用

由定理7.1.1知，若能求出

Δ_t+Δ_xX=X_xΔ （7.2.1）

的解Δ_k（t，x），则

与

等价.

例如，若X（t，x）=0，则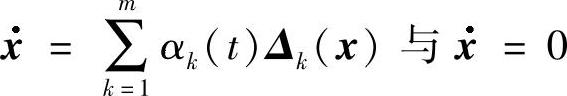等价，这里α_k（t）（k=1，2，…，m）为任意连续可微的奇函数.

一般情况要求出式（7.2.1）的解是非常困难的，在求不出解的情况，且不知道系统（7.2.3）的反射函数的表达式的前提下，又如何来构建一个微分系统（7.2.2），使得它与系统（7.2.3）等价呢？下面将讨论这个问题.

下面我们给出构造（7.2.2）的步骤

1.构造函数

Δ^（0）（t，x）∶=Y（t，x）-X（t，x），

Δ^（i+1）（t，x）∶=Δ_t^（i）+Δ_x（i）X_-XxΔ^（i），（i=0，1，2，…m）

2.寻找m个纯量函数b₀（t），b₁（t），…，b_m-1（t）使得

b₀（t）Δ^（0）（t，x）+b₁（t）Δ^（1）（t，x）+…+b_m-1（t）Δ^（m-1）（t，x）+Δ^（m）=0 （7.2.4）

成立.

由此可选择ln＞m，x_r=（x_1r，x_2r，…，x_nr）为任一点，有

b₀（t）Δ^（0）（t，x_r）+…+b_m-1（t）Δ^（m-1）（t，x_r）+Δ^（m）（t，x_r）=0 （r=1，2，…，l）.

3.求解式（7.2.4），若式（7.2.4）没有解，则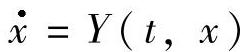就不具有形式（7.2.2），然后我们选择更大的m，重复上面同样步骤.现在我们假设式（7.2.4）有解b₀，b₁，…，b_m-1.

4.寻找奇的纯量线性无关的函数α₁（t），α₂（t），…，α_m（t）使得下面等式

b₀（t）α（t）+b₁（t）α′（t）+…+b_m-1（t）α^（m-1）（t）+α^m（t）=0，

-b₀（-t）α（t）+b₁（-t）α′（t）+…+b_m-1（-t）α^（m-1）（t）+（-1）^mα^m（t）=0

成立.(https://www.daowen.com)

5.从下面代数方程组中解出我们所需要的Δ₁（t，x），Δ₂（t，x），…，Δ_m（t，x），

6.若由式（7.2.5）所得的Δ₁（t，x），Δ₂（t，x），…，Δ_m（t，x）满足式（7.2.1），

则

与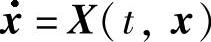等价.这个结论由定理7.1.3推得.

例7.2.1

则

要使上式右端为零向量，只要

b₀sint+b₁cost=sint， b₀sin3t+3b₁cos3t=9sin3t，

即取

解方程

b₀α+α′b₁+α″=0，

即

解该方程得α₁=sint，α₂=sin3_t.

解代数方程组

得

易验证，Y（t，x）=X（x）+sintΔ₁+sin3tΔ₂，且

Δ_1t+Δ_1xX-X_xΔ₁=0，

Δ_2t+Δ_2xX-X_xΔ₂=0.

即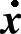=Y（t，x）与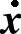=X（x）等价.