考虑微分系统

假设系统（7.1.1）右端满足解的存在唯一性定理的条件，并设F（t，x）为系统（7.1.1）的反射函数.由第2章，我们知道凡是与系统（7.1.1）等价的微分系统均可表示为

其中R（t，x）为任意连续可微的向量函数.

或者

且

F_x（t，x）S（t，x）+S（-t，F（t，x））=0. （7.1.4）不管是微分系统（7.1.2）还是系统（7.1.3）都要在F（t，x）已知的情况下，才能确定它们是否与系统（7.1.1）等价.本节我们将讨论在F（t，x）未知的情况下，如何判定系统（7.1.3）是否等价于系统（7.1.1），以及构造一个微分系统与（7.1.1）等价.

引理7.1.1 设

S（t，x）=（S₁（t，x），S₂（t，x），…，S_n（t，x））^T，

X（t，x）=（X₁（t，x），X₂（t，x），…，X_n（t，x））^T，

Y（t，x）=（Y₁（t，x），Y₂（t，x），…，Y_n（t，x））^T，x∈Rⁿ

为任意三个可微的向量函数，则成立等式

证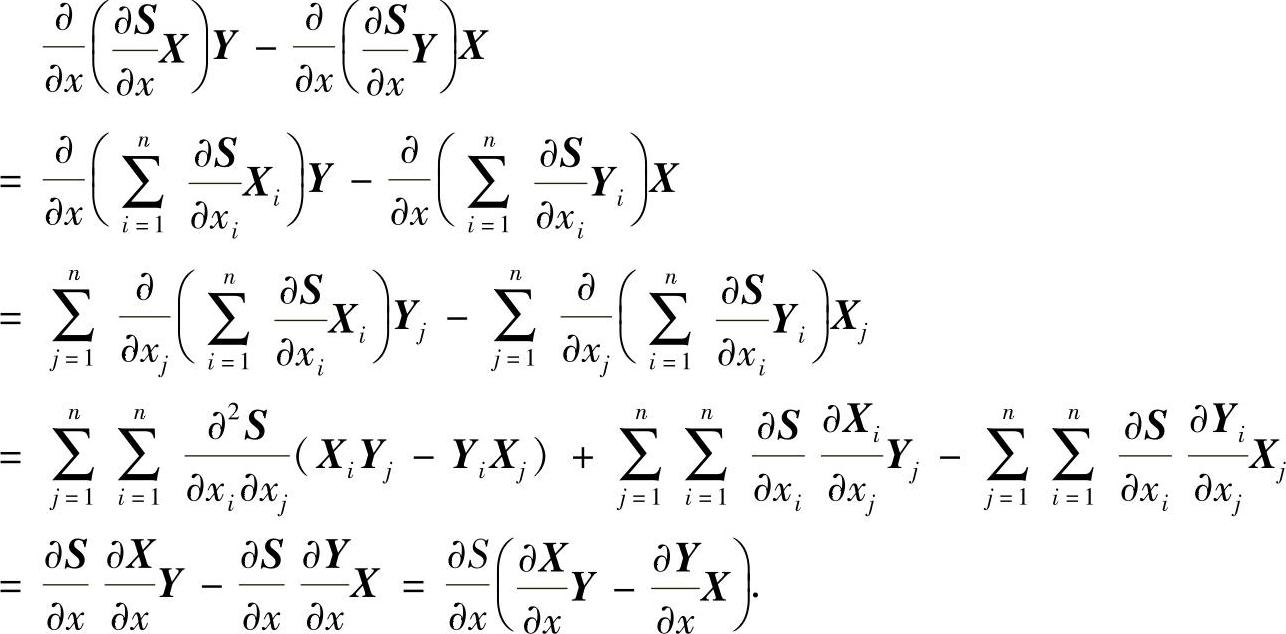

引理7.1.2 设F（t，x）为系统（7.1.1）的反射函数，对任意连续可微的向量函数Δ（t，x），函数

U（t，x）∶=F_x（t，x）Δ（t，x）-Δ（-t，F（t，x））

成立等式

其中Δ=Δ（-t，F（t，x））；X=X（-t，F（t，x））.

证 由于F（t，x）为系统（7.1.1）的反射函数，则

从而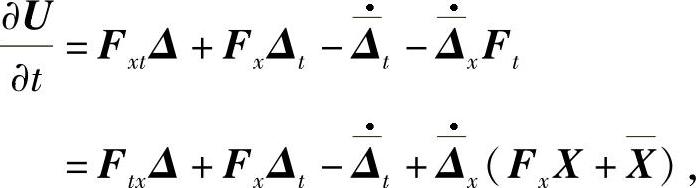则从而

则

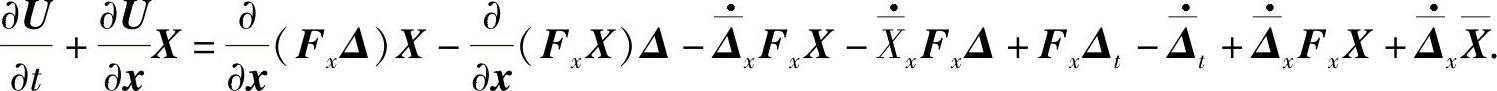
由引理7.1.1得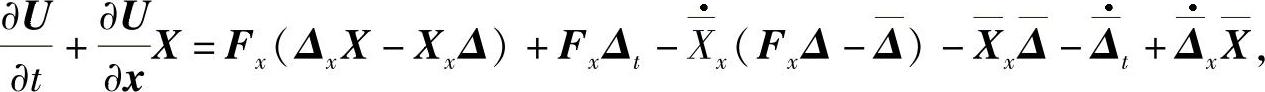

即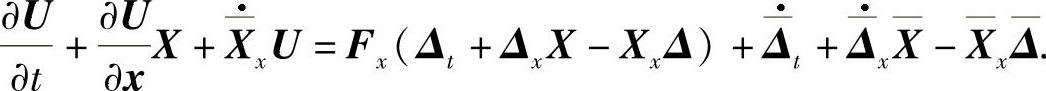

从而引理7.1.2得证.

定理7.1.1 若向量函数Δ（t，x）为偏微分方程

Δ_t+Δ_xX=X_xΔ （7.1.7）

的解，则微分系统

与系统（7.1.1）等价，其中α（t）为任意连续可微的纯量奇函数.

证 要证系统（7.1.8）与偏微分方程（7.1.1）等价，仅需证明

F_xα（t）Δ（t，x）+α（-t）Δ（-t，F（t，x））=0.

由于α（t）+α（-t）=0，则只需证明

F_xΔ（t，x）=Δ（-t，F（t，x）） （7.1.9）

即可.

事实上，由引理7.1.2及方程（7.1.7），我们知道，对于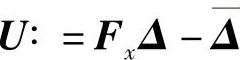成立

又U|_t=0=0，即U（t，x）为Cauchy问题

的解，由初值问题解的唯一性可得U≡0，即式（7.1.9）成立，从而定理得证.

推论7.1.1 假设Δ_k（t，x）为偏微分方程（7.1.7）的解，则微分系统

与系统（7.1.1）等价，其中α_k（t）（k=1，2，…）为任意连续可微的纯量奇函数，且上述微分系统的右端收敛于一个连续可微函数.

引理7.1.3 记

Δ_k（t，x）为方程（7.1.7）的解，α_k（t）为m次可微函数.又记

则

证 由定义可得

由于Δ_kt+Δ_kxX=X_xΔ_k，则(www.daowen.com)

同理可得.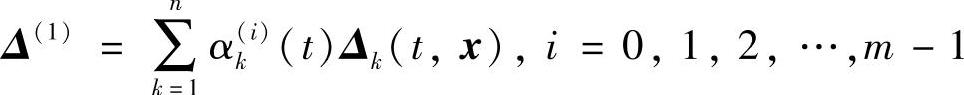

定理7.1.2 假设下列条件成立

（1）α₁（t），α₂（t），…，α_m（t）为R上线性无关的纯量奇m次可微函数；

（2）m次可微向量函数Δ_k（t，x）为方程（7.1.7）的解向量，则一定存在连续的纯量函数a₀（t），a₁（t），…，a_m（t）使得

a₀（t）Δ（0）（t，x）+a₁（t）Δ^（1）（t，x）+…+a_m（t）Δ^（m）（t，x）≡0，∀t，x， （7.1.12）其中Δ（i）（t，x）由式（7.1.11）定义，而且a_k（t）由下面的表达式表示

证 由于微分方程

有解α₁，α₂，…，α_m.

又由式（7.1.13）知，a₀，a₁，a₂，…，a_m为式（7.1.14）的左边行列式的第一行的代数余子式，从而方程（7.1.14）等价于

a₀z+a₁z′+a₂z″+…+a_mz^（m）=0. （7.1.15）

又由于α₁，α₂，…，α_m为式（7.1.15）的解，则有

a₀α_i+a₁α_i′+a₂α_i″+…+a_mα_i^（m）≡0 （i=0，1，2，…，m）

则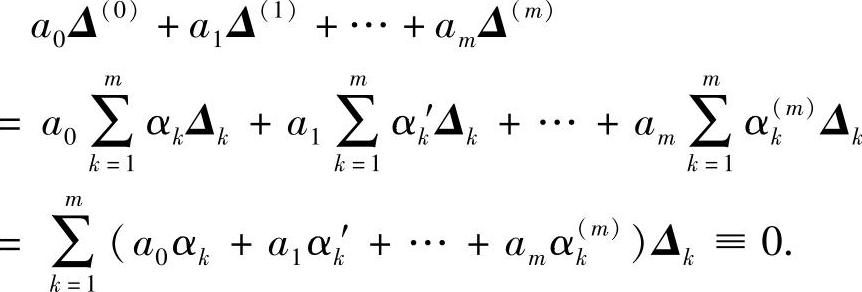

即式（7.1.12）成立.

定理7.1.3 假设对m次可微向量函数，存在纯量函数a₀（t），a₁（t），…，a_m（t）使得式（7.1.12）成立，其中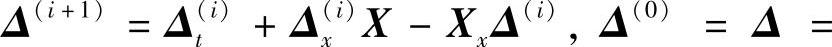

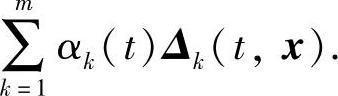
另外，线性微分方程

a₀（t）α（t）+a₁（t）α′（t）+…+a_m（t）α^（m）（t）=0 （7.1.16）

具有m次奇函数解α₁，α₂，…，α_m，并且这m个函数的Wronsky行列式仅在某些孤立点处为零.则微分系统

与系统（7.1.1）等价.

证 构造一个代数方程

由于该方程组的系数行列式不恒于零，则该方程组有唯一解（Δ₁，Δ₂，…，Δ_m）.

下面首先证明

Δ^（m）=α₁^（m）Δ_1+α2^（m）Δ₂+…+α_m^（m）Δ_m （7.1.19）

成立.事实上，由式（7.1.12）得

又由式（7.1.18）可得

再利用式（7.1.16）可得

a₀α_k+a₁α_k′+…+a_kα_k（m）=0 （k=1，2，…，m）

即

a₀α_k+a₁α_k′+…+a_m-1α_k^（m-1）=-a_mα_k^（m），

将此式代入前式可得

即式（7.1.19）成立.

从而有

应用式（7.1.20）可推得

由此推出

同理可得

记LΔ_k=Δ_kt+Δ_kxX-X_xΔ_k，则式（7.1.21）可表示为

即

由于代数方程组（7.1.22）的系数行列式非零，从而式（7.1.22）有唯一解

（LΔ₁，LΔ₂，…，LΔ_m）=（0，0，…，0），

即Δ_k（t，x）为系统（7.1.7）的解，从而由定理7.1.1得微分系统（7.1.17）与系统（7.1.1）等价.