考虑微分系统

x′=X（t，x），t∈R，x∈D⊂Rⁿ， （6.6.1）

y′=Y（t，y），t∈R，y∈G⊂Rⁿ， （6.6.2）D，G为Rⁿ内的一个区域.

假设微分系统（6.6.1）与系统（6.6.2）满足6.5节系统（6.5.1）中的条件（Ⅰ）和条件（Ⅱ）.设x（t，x₀）为系统（6.6.1）满足条件x（0，x₀）=x₀的解.y（t，y₀）为系统（6.6.2）满足条件y（0，y₀）=y₀的解.I₁（x₀），I₂（y₀）分别为解x（t，x₀），y（t，y₀）的最大存在区间.

记

为解x（t，x₀），y（t，y₀）的奇部.‖x‖为x的欧氏范数.

定义6.6.1 微分系统（6.6.1）与系统（6.6.2）称为奇⁃等价的，如果存在一一对应y₀=φ（x₀），φ∶D→G，并且I₁（x₀）=I₂（φ（x₀）），对∀t∈I₁（x₀）有

‖y_o（t，φ（x₀））‖=λ‖x_o（t，x₀）‖，

这里λ=λ（x₀）为某正的与t无关的数.

例6.6.1 微分系统

与微分系统

为奇⁃等价的.这里f，g为任意单值可微函数.

由于

‖x_o（t，x₀）‖²=‖x₀‖²sin²[f（‖x₀‖）t]，

‖y_o（t，y₀）‖²=‖y₀‖²sin²[g（‖y₀‖）t]，

x|_t=0=x₀=（x⁰₁，x⁰₂），y|_t=0=y₀=（y⁰₁，y⁰₂）.

令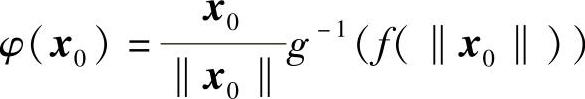，当x₀≠（0，0），φ（0，0）=（0，0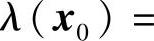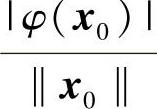）；，当x₀≠（0，0）；λ=1，当x₀=（0，0）.由定义6.6.1得以上二系统奇⁃等价.

定理6.6.1 若微分系统（6.6.1）与系统（6.6.2）奇⁃等价，则它们的2ω⁃周期解一一对应.

证 设微分系统（6.6.1）与系统（6.6.2）奇⁃等价，则

‖y₀（ω，φ（x₀））‖=λ‖x_o（ω，x₀）‖，

由此及由引理6.5.1得，微分系统（6.6.1）的2ω⁃周期解x（t，x₀）与微分系统（6.6.2）的2ω⁃周期解y（t，φ（x₀））一一对应.

在某些情况下，我们可以建立系统（6.6.1）与系统（6.6.2）的奇⁃等价，为此我们假设X（t，x），Y（t，y），可导3n次，并设系统（6.6.1）与系统（6.6.2）奇⁃等价，则存在映射y=Φ（t，x）使得系统（6.6.1）的解x（t），x（0）=x₀与系统（6.6.2）的解y（t），y（0）=φ（x₀）相对应，并满足

‖y_o（t）‖=λ‖x_o（t）‖.

由此推得

k=0，1，2，…，3n.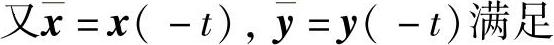

又由式（6.6.4），式（6.6.5）及式（6.6.3）得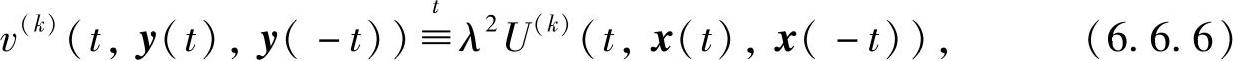

k=0，1，2，…，3n.

这里

解x（t）与y（t）之间的映射y=Φ（t，x）可由式（6.6.6）确定.

定理6.6.2 若微分系统（6.6.1）和系统（6.6.2）满足6.5节系统（6.5.1）中条件（Ⅰ）和条件（Ⅱ），且X（t，x），Y（t，y）具有3n次连续偏导，则它们奇⁃等价（y₀=φ（x₀）可微）的充要条件为微分方程组

k=0，1，2，…，3n.

对任意x₀∈D，（t，x）∈R×D，存在可微解

λ=λ（x₀），且满足条件

这里λ=λ（x₀）为正，x₀∈D，并满足关系式

F（0，x₀，λ（x₀））≡x₀，x₀∈D. （6.6.10）

证 必要性 设存在函数φ（x₀），λ（x₀）确定了微分系统（6.6.1）与系统（6.6.2）的奇⁃等价性.定义：

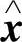
其中x（t；τ，x₀）和y（t；τ，x₀）为微分系统（6.6.1）和系统（6.6.2）的解.易验证F为微分系统（6.6.1）的反射函数，且对任意的λ，式（6.6.10）成立.设为系统（6.6.1）过（0，（0））的任一解，则由解的唯一性得x（0；t，.则

分别为微分系统（6.6.4），系统（6.6.2）和系统（6.6.5）的解.由此及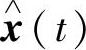的任意性得式（6.6.9）成立.

例证Φ（t，x）满足式（6.6.9）中第二式，事实上

即

由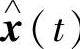）的任意性得

其余两式同理可证.

下证F，Φ，G满足关系式（6.6.8）.为此，注意到对于系统（6.6.1）的任一解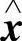（t），由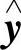（t）=Φ（t，（t））确定了系统（6.6.2）与之相对应的解.因为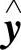（0）=y（0；0，φ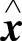（（0）））=φ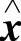（（0）），又由定理的条件得‖o（t）‖≡λ‖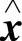o（t）‖，由此及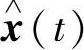的任意性即可推得式（6.6.8）成立，从而定理的必要性得证.

充分性 设F，Φ，G，λ满足关系式（6.6.8）～式（6.6.10），x（t）为系统（6.6.1）的解.定义新函数

由式（6.6.9）的第一式可得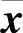，（t）为微分系统（6.6.4）的解.又x（-t）也是式（6.6.4）的解.另一方面由关系式（6.6.10）得

则由解的唯一性得

又由定理的条件得F，Φ，G满足关系式（6.6.8），特别地，有

V（0）（t，Φ，G）≡λ²U^（0）（t，x，F），

即

‖Φ-G‖²≡λ²‖x-F‖².

由此及式（6.6.11）和y（t）的定义得(www.daowen.com)

令t=0得.又由式（6.6.9）得（t）为系统（6.6.5）的解，y（-t）也是系统（6.6.5）的解，则由解的唯一性得，再由式（6.6.12）得

‖y（t）-y（-t）‖²=λ²‖x（t）-x（-t）‖²，

即

‖y_o（t）‖²=λ²‖x_o（t）‖²，

由此得微分系统（6.6.1）与系统（6.6.2）奇⁃等价.综上定理证毕.

推论6.6.1 若方程组

相对于变量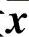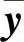，存在可微解

并满足

这里λ=λ（x₀），对任意x₀∈D为正的，且有

F（0，x₀，φ（x₀），λ（x₀））≡x₀，

φ∶D→G上函数.则满足6.5节系统（6.5.1）条件（Ⅰ）和条件（Ⅱ）的微分系统（6.6.1）与系统（6.6.2）奇⁃等价.

证 记Φ（t，x）为Cauchy问题

的解，则函数Φ（t，x），F（t，x，Φ（t，x），λ），G（t，x，Φ（t，x），λ）就与定理6.6.2中F，Φ，G一样满足该定理的条件，从而系统（6.6.1）与系统（6.6.2）奇⁃等价.

例6.6.2 应用上面的推论可以证明微分方程

与y′=cost为奇⁃等价的.此时式（6.6.8）1为

由此解出

由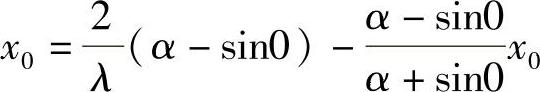解得，则此时，F，G满足推论中的所有条件，从而它们奇⁃等价.

设F（t，x）为微分系统（6.6.1）的反射函数，则有F（t，x（t））≡x（-t）.函数Φ（t，x，）为满足Φ（t，x，）-Φ（-t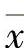，，x）≡x-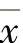的任意函数.（例如Φ（t，x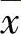，）=x+s（t）（x+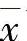）+R（t）（x-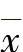），S（t）为偶函数，R（t）为奇的矩阵函数）.容易证明，若系统（6.6.2）为由系统（6.6.1）作变换y=Φ（t，x，F（t，x））所得的微分系统，则系统（6.6.1）与系统（6.6.2）奇⁃等价.

易验证微分方程

x′=x²+sint

与微分方程

y′=y²-sint的反射函数不相同，但它们是奇⁃等价的，由于它们的解满足关系式

y（t；-x₀）≡-x（-t；x₀）.

则当y₀=-x₀时有

y_o（t，y₀）≡x_o（t，x₀）.

故前两个方程为奇⁃等价.

定理6.6.3 假设函数F∶R×D→R，对任意t∈R满足

F（t，x₁，y₁）-F（t，x₂，y₂）＞0，

当x₁≥x₂，y₁≥y₂，（x_i，y_i）∈D，（x₁，y₁）≠（x₂，y₂）时，则微分方程

x″=F（t，x，x′）

最多只有一个周期解.

证 反证 设x₁（t），x₂（t）为该微分方程的两个周期解.为简单起见，设它们具有相同的周期（若x₁（t），x₂（t）具有不同的周期，同理可证）.

考察函数Z（t）=x₁（t）-x₂（t），则Z（t）为周期函数.从而下面几种情况之一成立.

1）Z（t）Z′（t）≤0，∀t∈R；

2）Z（t）Z′（t）=0，∀t∈R；

3）对某些t₀∈R，Z（t₀）Z′（t₀）＞0.

下面逐一讨论.

在第一种情况下，有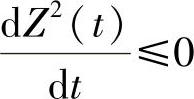，从而Z²（t）为单调递减函数，从而它不可能为周期函数，矛盾.

在第二种情况下，Z²（t）≡c，从而x₁（t）-x₂（t）≡c，即x₁（t）与x₂（t）=x₁（t）-c为前面方程的解，即

x₁″=F（t，x₁，x₁′），

x₂″=F（t，x₂，x₂′），

x₁″=F（t，x₁-c，x₁′），

由此推得F（t，x₁，x₁′）=F（t，x₁-c，x₁′）与定理的条件相矛盾.

在最后一种情况下，分两种情况讨论.

a）Z（t₀）＞0； b）Z（t₀）＜0.

若Z（t₀）＞0，则Z′（t₀）＞0，Z″（t₀）=F（t₀，x₁（t₀），x₁′（t₀））-F（t₀，x₂（t₀），x₂′（t₀））＞0.则一定存在t₁＞t₀，使得Z′（t）＞0不成立，否则，对∀t＞t₀，都有Z′（t）＞0，从而Z（t）为单调增函数，从而它不可能为周期函数，矛盾.从而一定存在t₀＜t₂≤t₁使得Z″（t₂）=0，Z（t₂）＞0，Z′（t₂）＞0.又Z″（t₂）=F（t₂，x₁（t₂），x₁′（t₂））-F（t₂，x₂（t₂），x₂′（t₂））＞0，矛盾.同理在Z（t₀）＜0时，同样可推得矛盾.综上得定理的结论成立.

推论6.6.2 若F（t，x，y）的偏导数F_x′，F_y′在R×D上存在且为正的，则定理6.4.3中方程的周期解的个数不超过一个.

证 由于F（t，x₁，y₁）-F（t，x₂，y₂）=F_x′（x₁-x₂）+F_y′（y₁-y₂）＞0，当x₁≥x₂，y₁≥y₂，（x₁，y₁）≠（x₂，y₂）时.从而由定理6.4.3推论成立.

推论6.6.3 线性方程

x″=a（t）x′+b（t）x+q（t）若a（t）＞0，b（t）＞0，t∈R，则该方程的周期解的个数不超过一个.