在研究微分系统周期解存在问题的过程中，常常会应用到该微分系统右端函数的对称性（奇性，偶性）或周期性^{[17，25，35，36]}，在此我们将感兴趣的部分介绍一下.

考虑微分系统

x′=X（t，x）=（X₁（t，x），X₂（t，x），…，X_n（t，x））^T，t∈R，x∈Rⁿ （6.5.1）

假设该微分系统满足如下条件：

（Ⅰ）X（t，x）连续可微，且其Cauchy问题的解存在唯一；

（Ⅱ）X（t+2ω，x）=X（t，x）.

引理6.5.1 设微分系统（6.5.1）满足条件（Ⅰ）和条件（Ⅱ），则在[-ω，ω]上有意义的解x（t）为2ω⁃周期的充要条件为x_o（ω）=0.这里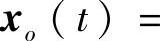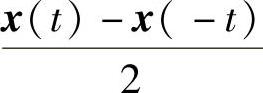为解x（t）的奇数部分.

证 设x（t）为系统（6.5.1）的2ω⁃周期解，则x（t+2ω）=x（t）.

从而必要性成立.

又设x（t）为系统（6.5.1）的解，且x_o（ω）=0，即x（ω）-x（-ω）=2x_o（ω）=0，则x（ω）=x（-ω）.

又x（t+2ω）也是系统（6.5.1）的解，且x（t+2ω）|_t=-ω=x（ω）=x（t）|_t=-ω，从而由Cauchy问题解的唯一性得x（t+2ω）=x（t）.即充分性成立.

由上引理知，确定系统（6.5.1）的解x（t）的周期性依赖于x（t）奇数部分，由此我们可以从研究x_o（t）奇数部分和偶数部分出发，进一步来研究x（t）.

由于x（t）=x_o（t）+x_e（t），若x（t）为系统（6.5.1）的解，则

x_e′（t）+x_o′（t）≡X（t，x_e（t）+x_o（t））. （6.5.2）

在式（6.5.2）中令t→-t得

-x_e′（t）+x_o′（t）≡X（-t，x_e（t）-x_o（t））. （6.5.3）

由式（6.5.2）和式（6.5.3）得

则向量函数

满足下面2n⁃维方程组

u（0）=x_e（0）=x（0），v（0）=x_o（0）=0.

我们称微分系统（6.5.5）为对应于微分系统（6.3.1）的奇⁃偶系统.

由条件（Ⅰ）可推得奇⁃偶系统的解唯一依赖于其初始条件，由此可推得下面的结论.

引理6.5.2 设函数X（t，x）连续可微，则向量函数（6.5.4）为奇⁃偶系统（6.5.5）满足条件u（0）=x（0），v（0）=0的唯一解.

一般情况下，奇⁃偶系统（6.5.5）要比系统（6.5.1）复杂，但是有时也能求出u（t），v（t），这样可以找出x（t）.

定理6.5.1 设微分系统（6.5.1）满足条件（Ⅰ）和条件（Ⅱ），并已知奇⁃偶系统（6.5.5）的积分流形v=Φ（t，u，v）满足Φ（ω，u，v）=Φ（-ω，u，-v），Φ关于t，u，v可微，则微分系统（6.5.1）满足条件x（0）=x₀的在[-ω，ω]上有定义的解x（t）为2ω⁃周期解，其中x（0）=x₀满足Φ（0，x₀，0）=0.

证 设微分系统（6.5.1）满足条件x（0）=x₀，Φ（0，x₀，0）=0，且在[-ω，ω]上有定义的解为x（t），下证x（t）=x（t+2ω）.

为此我们考察奇⁃偶系统（6.5.5）满足u（0）=x₀，v（0）=0的解（u（t），v（t））.由引理6.5.2知，u（t）=x_e（t），v（t）=x_o（t），则t=0，u（0）=x₀，v（0）=0在积分流形v=Φ（t，u，v）上，即v（0）=Φ（0，u（0），v（0））.则有v（t）≡Φ（t，u（t），v（t）），即

x_o（t）≡Φ（t，x_e（t），x_o（t））.(www.daowen.com)

令t=±ω得

x_o（ω）≡Φ（ω，x_e（ω），x_o（ω）），

-x_o（ω）=Φ（-ω，x_e（ω），-x_o（ω））.

再由定理的条件得

x_o（ω）=-x_o（ω），

从而有

x_o（ω）=0.

再由引理6.5.1得x（t）为2ω⁃周期解.

注6.5.1 若X（t，x）是关于t的奇函数，则相应于系统（6.5.1）的奇⁃偶系统（6.5.5）具有线性积分流形v=0.又若X（t+2ω，x）=X（t，x），则由定理6.5.1知，系统（6.5.1）在[-ω，ω]上有定义的解皆为2ω⁃周期解.

定理6.5.2 设微分系统（6.5.1）满足条件（Ⅰ）和条件（Ⅱ），对某个i，1≤i≤n，对所有（t，x）有

X_i（t，x）+X_i（-t，F（t，x））≠0.

则微分系统（6.5.1）不存在2ω⁃周期解，这里F（t，x）为系统（6.5.1）的反射函数.

证 设x（t）为系统（6.5.1）的任一解，则u（t）=x_e（t），v（t）=x_o（t）为式（6.5.5）的解.考察向量函数x_o（t）的分量x_io（t）.

即x_io（t）不变号，又由于x_io（0）=0，则对于t＞0，x_io（t）＞0（＜0），特别地，x_io（ω）＞0（＜0），则x_o（ω）≠0，从而由引理6.5.1得x（t）不可能为2ω⁃周期函数.

定理6.5.3 若微分系统（6.5.1）满足条件（Ⅰ）和条件（Ⅱ），且对于某个i，1≤i≤n和一切x∈Rⁿ有

X_i（ω，x）-X_i（-ω，F（ω，x））≠0，

则微分系统（6.5.1）不存在2ω⁃周期解.

证 由第2章基本引理2.1.1得，微分系统（6.5.1）的在[-ω，ω]有意义的解φ（t；-ω，x）为2ω⁃周期解的充要条件为F（-ω，x）=x.则对∀i，1≤i≤n有

X_i（ω，x）-X_i（-ω，F（ω，x））=X_i（ω，x）-X_i（-ω，x）=0.

由此即可推得定理的结论成立.

推论6.5.1 若微分系统（6.5.1）满足条件（Ⅰ）和条件（Ⅱ），对于某个i，1≤i≤n和所有（t，x）∈R¹⁺ⁿ满足

X_i（t，x）≠X_i（-t，F（t，x）），

则微分系统（6.5.1）不存在2ω⁃周期解.

证 若存在x使得F（-ωx，x）=x，则对任意i，1≤i≤n，有

X_i（-ω，x）-X_i（ω，F（-ω，x））=X_i（-ω，x）-X_i（ω，x）=0，即X_i（t，x）-X_i（-t，F（t，x））|_t=-ω=0.与假设矛盾，从而系统（6.5.1）不存在2ω⁃周期解.

例6.5.1 微分系统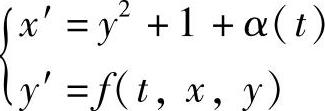，不存在2ω⁃周期解，这里α（t）为奇函数，α（t），f（t，x，y）为2ω⁃周期函数.由于，由定理6.5.2得该系统不存在2ω⁃周期解.