在本节中，我们主要应用反射函数法研究小参数系统

x′=A（t）x+P（t，x）+εR（t，x，ε）

周期解的存在性.应用拟反射函数研究小参数微分系统

周期解的存在性.

假设我们下面所讨论的微分系统都是2ω⁃周期系统且其初值问题的解的存在唯一，其中|ε|是小参数，E是单位矩阵.

定理6.4.1 假设F（t，x）是n维周期系统

x′=X（t，x，0） （6.4.1）

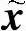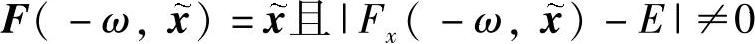的反射函数，存在使得，则对充分小的|ε|，周期系统

x′=X（t，x，ε）+F_x^-1（t，x）P（t，x）-P（-t，F（t，x）） （6.4.2）

存在有2ω⁃周期解.

证 由于

F_t（t，x）+F_x（t，x）X（t，x，0）+X（-t，F（t，x），0）=0， F（0，x）=x.容易验证F（t，x）也是周期系统

x′=X（t，x，0）+F_x^-1（t，x）P（t，x）-P（-t，F（t，x））

的反射函数.

令x=φ（t；t₀，x₀，ε）是系统（6.4.2）满足初时条件x（t₀）=x₀的解.则由反射函数的定义知，系统（6.4.2）的反射函数为G（t，x，ε）=φ（-t；t，x，ε），所以它的解x（t）是2ω⁃周期，当且仅当存在x₀使得

G（-ω，x₀，ε）=x₀， （6.4.3）

即

h（x₀，ε）∶=φ（ω；-ω，x₀，ε）-x₀=0.

又根据定理的假设得

由隐函数定理，存在常数ε₀＞0，使得当|ε|＜ε₀时，式（6.4.3）存在解x₀（ε）且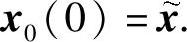从而，x=φ（t；-ω，x₀（ε），ε）是系统（6.4.2）的2ω⁃周期解.

若在定理6.4.1中，取F（t，x）=F（t）x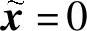，，则可推得下面的结论：

推论6.4.1 若F（t，x）=F（t）x是系统（6.4.1）的反射函数，|F（-ω）-E|≠0，则对充分小的|ε|，周期系统

x′=X（t，x，ε）+F（-t）P（t，x）-P（-t，F（t）x）

存在一个2ω⁃周期解.

现在考虑n维周期系统

x′=A（t）x+P（t）+εR（t，x，ε）， （6.4.4）

x′=A（t）x， （6.4.5）

其中A（t）=（a_ij（t））n×n.

定理6.4.2 若F（t，x）=F（t）x是系统（6.4.5）的反射函数，且|F（-ω）-E|≠0，则对充分小的|ε|，系统（6.4.4）存在2ω⁃周期解.

证 设X（t）是系统（6.4.5）的基解矩阵，则F（t）=X（-t）X^-1（t）.根据常数变易公式，系统（6.4.4）的解为

则系统（6.4.4）的反射函数为

记

h（x₀，ε）=G（-ω，x₀，ε）-x₀，

则

由于|F（-ω）-E|≠0，则有

h（x^∗，0）=0， deth_x（x^∗，0）≠0，

其中

由隐函数定理，存在常数ε₀＞0，使得当|ε|＜ε₀时，方程h（x₀，ε）=0有解x₀（ε），且x₀（0）=x^∗.因此，x=φ（t；-ω，x₀（ε），ε）是系统（6.4.4）的2ω⁃周期解.

注6.4.1 若我们不知道系统（6.4.5）的基解矩阵或者它的任一解，但是我们知道F（t，x）=F（t）x是系统（6.4.5）的反射函数，由定理6.4.2我们就能确定系统（6.4.4）的周期解的存在性.

例6.4.1 若在系统（6.4.5）中，取

则对于充分小的|ε|，微分系统（6.4.4）有一个2ω⁃周期解.其中γ_ij（i，j=1，2，…，n）是任意2ω⁃周期函数.

在上面的假设条件下，不难验证

是系统（6.4.5）的反射函数，且|F（-ω）-E|≠0.因此，由定理6.4.2可知该结论成立.

例6.4.2 易验证微分系统

的反射函数是

且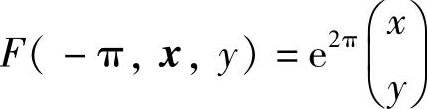，所以|F（-ω）-E|=（e^2π-1）²＞0.因此由定理6.4.2可知，对充分小的|ε|，周期系统

有一个2π⁃周期解

x=φ（t；-π，x₀（ε），y₀（ε），ε）， y=ψ（t；-π，x₀（ε），y₀（ε），ε）

且

定理6.4.3 设X（t）是系统（6.4.5）的基解矩阵且X（0）=E.若X（ω）X-1，且存在x^∗满足

则对充分小的|ε|，存在x₀=x₀（ε）满足x₀（0）=x^∗，且x=φ（t；-ω，x₀（ε），ε）是（6.4.4）的2ω⁃周期解，并有

证 由定理的假设和方程（6.4.6），有h（x₀，ε）=εX（ω）J（x₀，ε），这里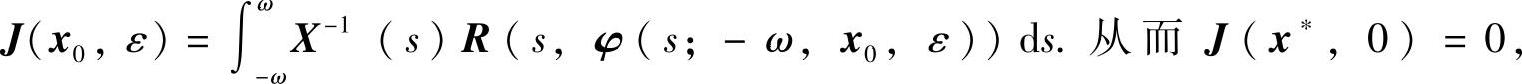|J_x（x^∗，0）|≠0.由隐函数定理，与定理6.4.2同理得，系统（6.4.4）存在2ω⁃周期解x=φ（t；-ω，x₀（ε），ε）.该解关于ε连续，由此关系式（6.4.7）成立.

现在我们将前面的定理应用到一个特殊的情况.

注6.4.2 在系统（6.4.4）中，若A（t）=0，P（t）=0，且存在x^∗满足

则对充分小的ε，x=φ（t；-ω，x₀（ε），ε）是系统（6.4.4）的2ω⁃周期解且

该结论与定理4.1[5，p.446]相同.

例6.4.3 微分系统

满足定理6.4.3的条件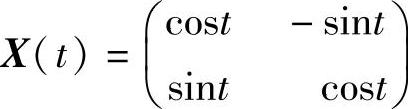，，其中r_i（t，x，y，ε）（i=1，2）为2π⁃周期函数.所以，对充分小的|ε|，系统（6.4.8）存在2π⁃周期解

x=φ（t；-π，x₀（ε），y₀（ε），ε）， y=ψ（t；-π，x₀（ε），y₀（ε），ε）且(www.daowen.com)

现在考虑二维周期系统

其中t，x，y∈R.设x=φ（t；t₀，x₀，y₀，ε），y=ψ（t；t₀，x₀，y₀，ε）是系统（6.4.9）满足条件x（t₀）=x₀，y（t₀）=y₀的解.

定理6.4.4 对于系统（6.4.9）

1）若存在可微函数Φ（t，x，y，ε）满足

Q（-t，Φ，-y，ε）=Q（t，x，y，ε），

Φ_t+Φ_xP（t，x，y，ε）+Φ_yQ（t，x，y，ε）+P（-t，Φ，-y，ε）=0，

且

Φ（0；x，0，ε）=Φ（kω；x，0，ε）=x.

2）当ε=0时，系统（6.4.9）有下面的解族

且存在一点x^∗使得ψ（kω；0，x^∗，0，0）=0，ψ_x（kω；0，x^∗，0，0）≠0.

则对于充分小的|ε|，存在x₀=x₀（ε）满足x₀（0）=x^∗，系统（6.4.9）有2kπ⁃周期解

且

证 由定理的条件，不难证明函数F（t，x，y）=（Φ，-y）^T满足

F_t（t，x）+F_x（t，x）X（t，x）+X（-t，F（t，x））=0，F（0，x₀，0）=（x₀，0）^T.从而由定理6.3.2知，系统（6.4.9）的解（6.4.10）为2kπ⁃周期，当且仅当，F（kω，x（kω），y（kω））=（x（kω），y（kω））^T，也就是y（kω）=0，即ψ（kω；0，x₀，0，ε）=0.由于ψ（kω；0，x^∗，0，0）=0，ψ_x（kω；0，x^∗，0，0）≠0，由隐函数定理可知，对充分小的|ε|，方程ψ（kω；0，x₀，0，ε）=0有解x₀=x₀（ε）且x₀（0）=x^∗.从而系统（6.4.10）有2kπ⁃周期解.

现在考虑周期系统

设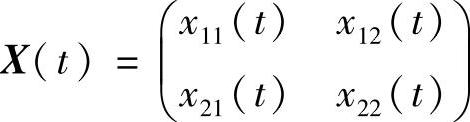是式（6.4.12）的基解矩阵且X（0）=E，W（t）=detX（t）.

推论6.4.2 对于系统（6.4.11），若

a₁₁（t）+a₁₁（-t）=0， a₂₂（t）+a₂₂（-t）=0，

a₁₂（t）=a₁₂（-t）， a₂₁（t）=a₂₁（-t），

r₁（t，x，y，ε）+r₁（-t，x，-y，ε）=0， r₂（t，x，y，ε）=r₂（-t，x，-y，ε），则：

1）若x₂₁（ω）≠0，则对充分小的|ε|，存在x₀=x₀（ε）使得x₀（0）=0，系统（6.4.11）有一个2ω⁃周期解

x=φ（t；0.x₀（ε），0，ε）， y=ψ（t；0.x₀（ε），0，ε），

且

2）若x₂₁（ω）=0且存在一点x^∗满足J（x^∗，0）=0，J_x（x^∗，0）≠0，其中

其中

φ₁=φ（s；0，x₀，0，ε）， ψ₁=ψ（s；0，x₀，0，ε），则对充分小的|ε|，存在x₀=x₀（ε）使得x₀（0）=x^∗，系统（6.4.11）有一个2ω⁃周期解

x=φ（t；0，x₀（ε），0，ε）， y=ψ（t；0.x₀（ε），0，ε），

且

证 根据上述的假设，可以看出F（t，x，y）=（x，-y）T是系统（6.4.11）的拟反射函数.从而由定理6.4.4，式（6.4.10）是系统（6.4.11）的2ω⁃周期解，当且仅当，ψ（ω；0，x₀，0，ε）=0.

另一方面，我们有

由上可知：

1）若x₂₁（ω）≠0，则ψ（ω，0，0，0）=0，ψ_x（ω，0，0，0）≠0.与定理6.4.4同理可得上面的结论成立.

2）若x₂₁（ω）=0，则ψ（ω，0，x₀，ε）=εx₂₂（ω）J（x₀，ε）.在这种情况下，与上定理同理可得结论成立.

类似地，我们可以得到下面的结论.定义微分系统

推论6.4.3 对于系统（6.4.13），若

a₁₁（t）+a₁₁（-t）=0， a₂₂（t）+a₂₂（-t）=0，

a₁₂（t）=a₁₂（-t）， a₂₁（t）=a₂₁（-t），

r₁（t，x，y，ε）+r₁（-t，x，-y，ε）=0， r₂（t，x，y，ε）=r₂（-t，x，-y，ε），

p₁（t）+p₁（-t）=0， p₂（t）=p₂（-t）.

则：

1）若x₂₁（ω）≠0，则对充分小的|ε|，存在x₀=x₀（ε）使得

系统（6.4.13）有2ω⁃周期解

x=φ（t；0，x₀（ε），0，ε）， y=ψ（t；0，x₀（ε），0，ε）

且

2）若x₂₁（ω）=0且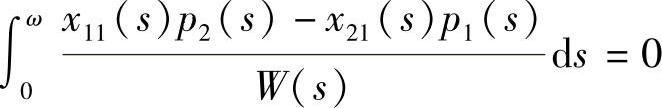，存在一点x∗使得J（x^∗，0）=0，J_x（x^∗，0）≠0，其中J（x₀，ε）与推论6.4.2的相同，则结论与情形1相同.

例6.4.4 微分系统

其中

r₁（t，x，y，ε）+r₁（-t，x，-y，ε）=0， r₂（t，x，y，ε）=r₂（-t，x，-y，ε），且r_i（t，x，y，ε）（i=1，2）是2π⁃周期函数.基解矩阵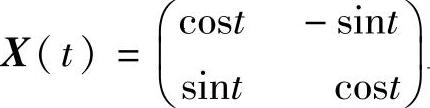且x₂₁（π）=0.通过简单计算可得J（0，0）=0，J_x（0，0）≠0，从而，对充分小的|ε|，该系统有2ω⁃周期解.

推论6.4.4 系统

若r₁（t，x，y，ε）=r₁（-t，-x，y，ε），r₂（t，x，y，ε）+r₂（-t，-x，y，ε）=0且存在一点y^∗满足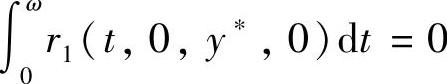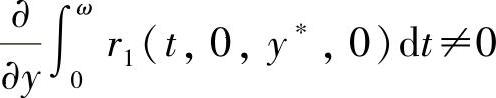，，则对充分小的|ε|，系统（6.4.14）有一个2ω⁃周期解

x=φ（t；0，0，y₀（ε），ε）， y=ψ（t；0，0，y₀（ε），ε），

且

证 微分系统（6.4.14）的解可表示为

根据定理的假设，可知F（t，x，y）=（-x，y）T是系统（6.4.14）的拟反射函数.因此，解（6.4.15）是2ω⁃周期，当且仅当，x（0）=0且x（ω）=0，即x₀=0且

由于_μ（y^∗，0）=0且μ_y0（y^∗，0）≠0，所以，对充分小的|ε|，方程μ₀（y₀，ε）=0存在一个解y₀=y₀（ε），从而系统（6.4.14）至少有一个2ω⁃周期解.

注6.4.3 容易看出形如（6.4.14）的系统不满足定理4.1[5，p.446]，但是由推论6.4.3可得这个系统有周期解.看下面的例子.

例6.4.5 由推论6.4.4可知，对充分小的|ε|，系统

有一个2π⁃周期解，其中μ_i（t，x，y，ε）（i=1，2）是关于t的2π⁃周期函数且μ₁（t，x，y，ε）=μ₁（-t，-x，y，ε），μ₂（t，x，y，ε）+μ₂（-t，-x，y，ε）=0.