这一节我们将利用反射函数理论来研究微分系统的解关于某些变量的对称性以及奇偶性.

定义6.1.1 对于一个向量函数族

x=φ（t，c），x^T=（x₁，…，x_n），c=（c₁，…，c_m）∈G，t∈（-α，α），α=α（c）， （6.1.1）

构造一个集合

G₀={（t，x）∶∃c∈G，t∈（-α，α），x=φ（t，c）}.

若存在函数x=F（t，x），（t，x）∈G₀，满足，t∈（-α，α），则称函数F（t，x）为函数族（6.1.1）的反射函数.

不是每个函数族都有反射函数，即使存在也不一定唯一.例如函数族x=c₁+c₂t，该函数族没有反射函数.若有，则F（t，c₁+c₂t）≡c₁-c₂t，由此，取c₁=t=1，c₂=0得，F（1，1）=1.取c₂=t=1，c₁=0得，F（1，1）=-1，矛盾，故函数族x=c₁+c₂t不存在反射函数.

又例如函数族x=ccost，y=-csint具有无穷多个反射函数.事实上，具有下列形式

x′=y+（xsint+ycost）f（t，x，y），y′=-x

的微分系统的反射函数

皆是函数族x=ccost，y=-csint的反射函数.

特别当m=n，α与c无关，函数c|→φ（t，c），对于每个固定的t具有反函数f（t，c），此时函数族x=φ（t，c）的反射函数存在且唯一，并且表示式为F（t，x）=φ（-t，f（t，x））.对于微分系统

x′=X（t，x）， （6.1.2）

若X（t，x）连续可微且其初值问题的解存在唯一，此时其解族的反射函数存在且唯一，并与微分系统（6.1.2）的反射函数相同.

我们感兴趣的是，若函数族（6.1.1）的表达式没有给出，而且知道它是某个微分系统的解族，那如何研究它的几何性态呢？

为了研究上述问题，我们考虑微分系统

x′=P（t，x，y）， y′=Q（t，x，y）. （6.1.3）

假设P（t，x，y），Q（t，x，y）在R³上连续可微，其通解为x=x（t，c₁，c₂），y=y（t，c₁，c₂）.为了简单起见，我们在R³上考虑微分系统（6.1.3），且假设其解在R上有意义.取函数族（6.1.1）为x（t，c₁，c₂），即微分系统（6.1.3）解的第一分量.现在要问，何时这第一分量是t的偶函数？用反射函数的语言来说即：何时这个函数族的反射函数具有这样形式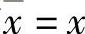？下面两个定理将回答该问题.

定理6.1.1 若微分系统（6.1.3）的一切解（x（t），y（t））的第一分量为t的偶函数，则该系统的反射函数具有形式

（F₁，F₂）=（x，F₂（t，x，y））， （6.1.4）

其中F满足

F₂（0，x，y）=y； （6.1.5）

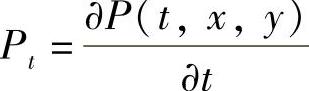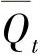这里，，Q1，同理.

证 设F=（F₁（t，x，y），F₂（t，x，y））^T为微分系统（6.1.3）的反射函数，则由反射函数的性质（第2章2.1节）得

F₁（t，x（t），y（t））≡x（-t）， F₂（t，x（t），y（t））≡y（-t）.又由于x（t）为偶函数，则F₁=x.即

P（t，x，y）+P（-t，x，F₂（t，x，y））=0，

将式（6.1.6）关于t，x，y求导得

将式（6.1.8）乘以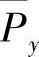并应用上述结论即可推得式（6.1.7）成立.从而定理得证.

定理6.1.2 假设对微分系统（6.1.3），存在连续可微函数F₂（t，x，y）满足条件（6.1.5）～条件（6.1.7），且P_y（-t，x，F₂（t，x，y））≠0，则微分系统（6.1.3）具有形如式（6.1.4）的反射函数，且有x（t）=x（-t）.

证 由于F₂（t，x，y）满足式（6.1.6），则由隐函数求导得式（6.1.9）成立.将式（6.1.9）代入式（6.1.7）可得

又，则

综合式（6.1.5）和式（6.1.6）及此式即可得F=（x，F₂（t，x，y））^T为微分系统（6.1.3）的反射函数.又由反射函数的性质知x（t）≡x（-t）成立，从而定理得证.

定理6.1.3 假设定理6.1.2的条件成立，并且微分系统（6.1.3）为关于t的2ω⁃周期系统，则其在[-ω，ω]上有意义的解皆以2ω为周期.

该定理的结论可由反射函数的基本引理2.1.1推得.

定理6.1.4 设v（t，x）关于（t，x）m次连续可导，并满足

这里f为一个连续可微函数，并且

f（-t，y₁，-y₂，…，（-1）^m-1y_m）≡（-1）^mf（t，y₁，y₂，…，y_m），

而

而对微分系统（6.1.2）满足条件

的解x（t）有

证 由定理的条件得，对微分系统（6.1.2）的解x（t），v（t）∶=v（t，x（t））和v（-t）∶=v（-t，x（-t））皆是微分方程（6.1.10）的解，且在t=0时，初始值相等，则由解的唯一性得v（t，x（t））=v（-t，x（-t））成立.

注6.1.1 同理我们可以证明，若函数f满足

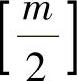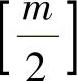f（-t，-y₁，y₂，…，（-1）^my_m）≡（-1）^m+1f（t，y₁，y₂，…，y_m）并且v（t，x）满足式（6.1.10），则有v（t，x（t））=-v（-t，x（-t））.其中x（t）为式（6.1.2）满足条件v^（2k）（0，x（0））=0，k=0，1，…，的解.这里为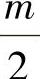的整数部分.

对于函数族（6.1.1），当m＞n时，其反射函数可能不存在，然而我们可以增加向量x的维数x_k（t，c₁，c₂，…，c_m），k=n+1，n+2，…，m，这样可得到新的函数族，它可能有反射函数.

例如，考虑二阶微分方程组

x″+A（t）x′+B（t）x=0，x∈Rⁿ （6.1.11）

其解族依赖于2n个参数.因此在一般情况下，它没有反射函数.但是，如果考虑新的函数族x（t），y∶=x′（t），它是一阶微分系统x′=y，y′=-Ay-Bx的解族，它是具有反射函数的.而对于微分方程组（6.1.11）是没有反射函数的.若存在反射函数x=F（t，x），则对式（6.1.11）的任一解x（t）有(www.daowen.com)

-x′（-t）=F_t（t，x（t））+F_x（t，x（t））x′（t），

令t=0得

F_t（0，x（0））+（F_x（0，x（0））+E）x′（0）=0，

显然该等式不可能对所有的x（0），x′（0）以及满足x（-t）=F（t，x（t））的x（t）成立.

现在我们来寻找微分系统（6.1.11）的子解族，具有形如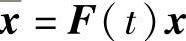的反射函数，则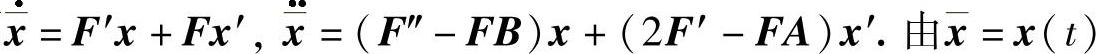满足方程x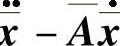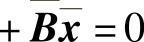，则有

则若

成立，则上式成立.

又由x=F（t）x，则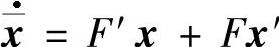，令t=0得F（0）=E，2x′（0）=-F′（0）x（0）=-A（0）x（0）.不难证明，若2A′+A²-4B≡m（t）E（m（t）为一个偶的纯量函数），则关系式（6.1.12）成立.

定理6.1.5 假设对于两个n×n阶矩阵A，B，存在纯量函数α_i（t），使M∶=2A′+A²-4B满足

则微分系统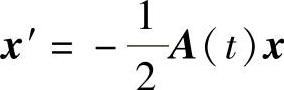的反射函数x=F（t）x也是微分系统（6.1.11），满足条件2x′（0）=-A（0）x（0）的解族的反射函数，且F（t）满足关系式（6.1.12）和F（0）=E.

证 令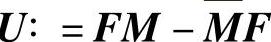（这里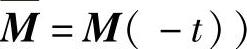.则通过计算可得

又由于U（0）=0，故由线性方程Cauchy问题解的唯一性可得，U（t）≡0.

对于微分系统（6.1.11）满足条件2x′（0）=-A（0）x（0）的解x（t），令V（t）∶=x（-t）-F（t）x（t），则有

V″=A（-t）V′-B（-t）V.

又由于V（0）=0，则由解的唯一性得，V（t）≡0.即x（-t）≡F（t）x（t）.从而定理得证.

推论6.1.1 若定理6.1.5的条件成立，且2ω⁃周期系统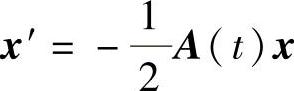不稳定，则2ω⁃周期系统（6.1.11）也不稳定.

证 由于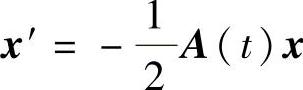不稳定，则存在一个无界解x（t），对于这个解，Poincaré映射x（ω）=F（-ω）x（-ω）也无界，即F^k（-ω）x（-ω）为发散序列，由此即可推得推论的结论成立.

定理6.1.5的结论也可推广到m阶微分系统^[151]

x^（m）+A₁（t）x^（m-1）+…+A_m（t）x=0. （6.1.13）

其中A_i（t）为n×n阶连续可微矩阵t∈R（i=1，2，…，m），x=（x₁，x₂，…，x_n）^T∈Rⁿ.

定理6.1.6 若对于矩阵函数A_i（t）（i=1，2，…，m）存在连续可微的纯量奇函数α_j（t），β_2j+1（t）和偶函数β_2j（t）（j=0，1，2，…）满足当k=2l-1时，

当k=2l时，

其中

则微分系统

的反射函数x=F（t）x也是微分系统（6.1.13）满足条件

的解族的反射函数.并且此时F满足

并且当2ω⁃周期系统不稳定时，2ω⁃周期系统（6.1.13）也不稳定.

该定理的证明可见参考文献[151].

定理6.1.7 假设连续可微函数F（t，x），（t，x）∈D⊂R¹⁺ⁿ，0∈D，满足

P（-t，F（t，x），x）+Q（t，x，F（t，x））=0， （6.1.14）

F_t+F_xP（t，x，F）≡Q（t，x，F），F（0，x）=x. （6.1.15）

则对微分系统（6.1.3）满足条件y（0）=x（0）的解x（t），y（t）成立y（t）≡F（t，x（t））≡x（-t）.并且若系统（6.1.3）为2ω⁃周期系统时，则其在[-ω，ω]上有意义的解x（t）为2ω⁃周期解的充要条件为F（-ω，x（ω））=x（ω）.

证 由式（6.1.15）可推得微分系统（6.1.3）满足条件y（0）=x（0）的解x（t），y（t）满足y（t）≡F（t，x（t）），其中x（t）为微分系统

x′=P（t，x，F（t，x）） （6.1.16）

的解.则由式（6.1.14）和式（6.1.15）推得F（t，x）为系统（6.1.16）的反射函数，则有F（t，x（t））=x（-t），从而得y（t）≡F（t，x（-t））=x（-t）成立.当微分系统（6.1.3）为2ω周期系统时，由于

（x（-ω），y（-ω））=（x（-ω），F（-ω，x（-ω）））=（x（-ω），x（ω）），

由此及基本引理2.1.1即得定理6.1.7正确.

定理6.1.8 设f∶Rⁿ|→Rⁿ，g∶R¹⁺ⁿ→R连续可微函数，并且g是关于t的2ω⁃周期函数，且满足g（-t，y，x）+g（t，x，y）≡0，则微分系统

z′=f（z） （6.1.17）

的任一2αω⁃周期解z（t）确定微分系统

满足条件x（αω）=y（-αω）=z（0）的解x（t），y（t）的有界性.且当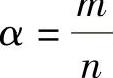为不可约有理分数时，这些解为2mω⁃周期解.

证 由于系统（6.1.17）为自治系统，从而它为简单系统（见2.3节中定义2.3.3），则其反射函数F（t，x）满足关系式F_t=-2f（F），F_xf（x）≡f（F）.由此可推出F（t，x）也是微分系统

x′=f（x）（g（t，x，F（t，x））+1） （6.1.19）

的反射函数.

设φ（t-t₀；0，z₀）为微分系统（6.1.17）的解，则F（t，z）≡φ（-2t；0，z）.若φ（t；0，z₀）为2αω⁃周期，F（t，z）为αω⁃周期，从而有F（-αω，z₀）=F（0，z₀）=z₀，且对任意正整数r有F（-αrω，z₀）=z0.

令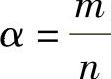，对于t∈R，x∈G，G为微分系统（6.1.17）解φ（t；0，z₀）的轨迹所形成的点集.微分系统（6.1.19）为关于t的2mω⁃周期系统.由于F（-mω，z₀）=F（-nαz₀，z₀）=z₀，即z₀为不动点，因此微分系统（6.1.19）满足条件x（mω）=z₀的解x（t）为2mω⁃周期解.又由定理6.1.7得，对于微分系统（6.1.18）条件（6.1.13）和条件（6.1.14）满足，则有y（t）≡x（-t）.微分系统（6.1.18）满足条件x（αω）=y（-αω）=z₀的解x（t），y（t）的有界性可由（x（t），y（t））∈G推得，综上定理得证.