考虑多项式微分系统

这里p_i（t，x），q_j（t，x）（i=0，1，2；j=0，1，2，…，n）为连续可微函数且保证微分系统（5.2.1）的Cauchy问题解存在且唯一.（在参考文献[145]中讨论了n=2的情形）

这一节我们简记：

下文中提到的“p_i（t，x）≠0”表示在t=0的充分小的去心领域中p_i（t，x）≠0.

在这一节我们将讨论当系统（5.2.1）的反射函数F（t，x，y）=（F₁（t，x，y），F₂（t，x，y））^T中的F₁（t，x，y）=x时，F₂（t，x，y）的结构形式.

引理5.2.1 若F₁=x，则

p_i（0，x）=0， i=0，1，2. （5.2.2）

证 由于F（t，x，y）=（x，F₂）^T为系统（5.2.1）的反射函数，则

P（t，x，y）+P（-t，x，F₂）≡0，

即

A₀+A₁F₂+A₂F²₂≡0， （5.2.3）

其中

在式（5.2.3）中，取t=0，得

p₀（0，x）+p₁（0，x）y+p₂（0，x）y²≡0 （∀x，y）

由此即可推出式（5.2.2）成立.

在这一节里我们总假设式（5.2.2）成立.

引理5.2.2 对于系统（5.2.1），若F₁=x，且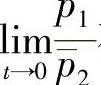存在，则

证 由式（5.2.3），可得

由于F₂（0，x，y）=y，由此及上式不难推出引理5.2.2的结论成立.

引理5.2.3 若

F²₂=a₀+b₀F₂， （5.2.4）

则

F²₂+k=a_k+b_kF₂.（5.2.5）

其中

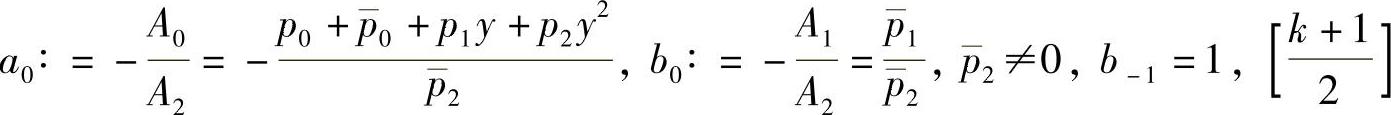为取整函数.

证 我们用数学归纳法来证明上述结论成立.由式（5.2.4）得

F₂³=a₀F₂+b₀F²₂=a₀b₀+（a₀+b²₀）F₂=a₁+b₁F₂，即式（5.2.5）当k=1时成立.

现假设k=m时，式（5.2.5）成立.即

F²₂+m=a_m+b_mF_2.下证，k=m+1时，式（5.2.5）也成立.

事实上，由上式得

F²₂+m+1=a_nF₂+b_nF²₂=a₀b_m+（b₀b_m+a_m）F₂=a_m+1+b_m+1F₂，其中

a_m+1=a₀b_m，

由于

C^j_m+1-j+C^j_m^-₊¹_1-j=C^j_m+2-j，

则

即式（5.2.5）对k=m+1也成立.从而引理的结论成立.

引理5.2.4 若e_k=2b_k-1-b₀b_k-2，k=1，2，3，…

则

证 由引理5.2.3，计算可得

即引理5.2.4的结论成立.

引理5.2.5 若Δ_k（t，x，y）=2a₀e_k-1+b₀e_k，则

其中Δ（t，x，y）=4a₀+b₀².

证 由引理5.2.4，我们可得

由于

则

同理可得

则

该引理得证.

定理5.2.1 对于系统（5.2.1），若F₁=x，则

（1）若p₂≡0，p₁≠0，则有F₂=f₂₀（t，x）+f₂₁（t，x）y；

（2）若p₂≠0，且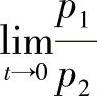存在，则F₂=f₂₀（t，x）+f₂₁（t，x）y.这里f₂₀（t，x），f₂₁（t，x）是R²上连续可微函数.

证 若p₂≡0，p₁≠0，由式（5.2.3），可得(www.daowen.com)

若p₂≠0，将式（5.2.3）沿着系统（5.2.1）的解求导得

DA₀+DA₁F₂+DA₂F²₂-A₁Q（-t，x，F₂）-2A₂Q（-t，x，F₂）F₂=0，

即

其中

由引理5.2.3得F²₂^+k=a_k+b_kF₂，k=1，2，…，n-1，a_k，b_k由式（5.2.6）表示，将此代入式（5.2.7）得

C₀+C₁F₂=0， （5.2.8）

其中

C₀=B₀+B₂a₀+B₃a₁+…+B_n+1a_n-1； （5.2.9）

C₁=B₁+B₂b₀+B₃b₁+…+B_n+1b_n-1. （5.2.10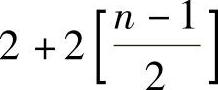）次多项式，C₁是关于y的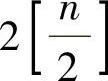次多项式.由式（5.2.8）得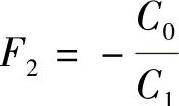，把此式代入式（5.2.3）得

C₁（A₀C₁-A₁C₀）=-A₂C²₀，

由此可推出C₁/C₀或C₁/A₂，从而

将此式代入式（5.2.3），并比较等式两边y的同次幂系数得

因此F₂=f₂₀（t，x）+f₂₁（t，x）y.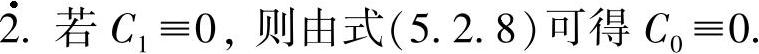

再由式（5.2.9）和式（5.2.10）计算可得

应用式（5.2.11）和式（5.2.12）计算可得

由引理5.2.5可得

又由于

其中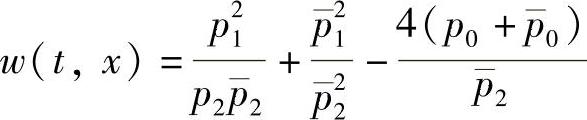.显然

再应用式（5.2.13）可得

这里R（t，x）是R²上连续可微函数.

又由引理5.2.2可得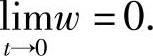则由Cauchy问题

解的唯一性定理得w（t，x）≡0.

因此

从而由式（5.2.3）可解出

从而定理结论成立.

定理5.2.2 如果下列条件满足

则函数F=（x，f₂₀（t，x）+f₂₂₁（t，x）y）^T为系统（5.2.1）的反射函数，其中当p₂≡0，p₁≠0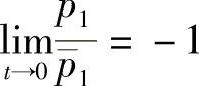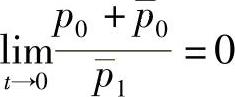，，时，

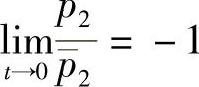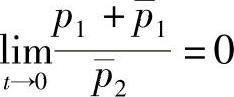当p₂≠0时，，时，

该定理的证明，只要验证F=（x，f₂₀（t，x）+f₂₁（t，x）y）^T反射函数的基本关系式

成立即可，容易检验在定理的条件下，上式成立.

定理5.2.3 若定理5.2.2的条件满足，且系统（5.2.1）为关于t的2ω-周期系统，则该微分系统所有在[-ω，ω]上有意义的解皆为2ω-周期解.

证 由定理5.2.2知系统（5.2.1）的Poincaré映射为

T（x，y）=F（-ω，x，y）=（x，f₂₀（-ω，x）+f₂₁（-ω，x）y）^T.

由于

f₂₁（t，x）f₂₁（-t，x）=1，f₂₀（-t，x）+f₂₀（t，x）f₂₁（-t，x）=0.

则

α（t，x）+α（-t，x）=0，β（t，x）+β（-t，x）=0，

且

α（t，x）=α（t+2ω，x），β（t，x）=β（t+2ω，x），

从而有

α（-ω，x）=0，β（-ω，x）=0.

因此

F（-ω，x，y）≡（x，y）^T.

故定理5.2.3的结论成立.

例5.2.1 微分系统

具有反射函数F（t，x，y）=（x，ye^2sint）^T，其中γ_i（t，x），δ_i（t，x）（i=0，1，2）为R²上任意连续可微的奇的2ω-周期函数.由定理5.2.3知，这个微分系统在[-ω，ω]上有意义的解皆为2ω-周期解.

例5.2.2 微分系统

具有反射函数F（t，x，y）=（x，F₂）^T，其中

F₂=ye^2sint+xsinte^sint（1+x²sin²t），

α_i=α_i（t，x），β_j=β_j（t，x）（i=0，1，2；j=0，1，…，n）为R²上任意连续可微函数.

又若α_i，β_i为t的2ω-周期函数，则由定理5.2.8知，该微分系统在[-ω，ω]上有意义的解皆为2ω-周期解.