在这一小节我们讨论微分系统

（a_i∶=a_i（t），b_i∶=b_i（t），i=1，2，…，5连续可微函数t∈R）.当该系统的反射函数的第一分量为f（t）x时，其第二分量具有什么样的形式？同时给出了该微分系统解的第一分量为偶函数的充要条件.

设系统（5.1.1）具有反射函数：F（t，x，y）=（F₁（t，x，y），F₂（t，x，y））^T.

引理5.1.1 若F₁（t，x，y）=f（t）x，则

f′（0）+2a₁（0）=0，a_i（0）=0（i=2，3，4，5）. （5.1.2）

证 若F₁（t，x，y）=f（t）x，则由反射函数的基本关系式得

这里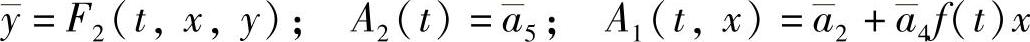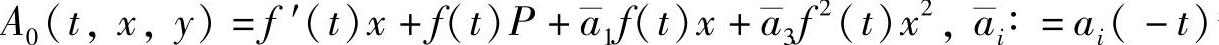；等.令t=0，则有

f′（0）x（0）+2[a₁（0）x（0）+a₂（0）y（0）+a₃（0）x²（0）+a₄（0）x（0）y（0）+a₅（0）y²（0）]^∀x（0）≡，^y（0）0.

由此推得引理的结论成立.

在这一节中，我们总假设条件（5.1.2）成立.记号a（t）≠0表示在t=0的某去心邻域里且t充分小成立.

引理5.1.2 若F₁（t，x，y）=f（t）x， a₅（t）≡0， a²₂（t）+a²₄（t）≠0，则F₂（t，x，y）=g₀（t，x）+g₁（t，x）y，

其中g₀（t，x），g₁（t，x）为连续可微函数，（t，x）∈R^2.

证 若F₁（t，x，y）=f（t）x，则由式（5.1.3）得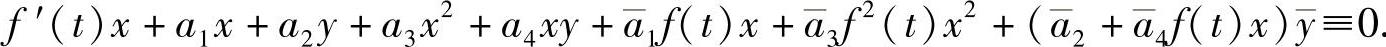

若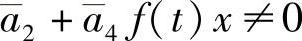，则由此推得F₂（t，x，y）=g₀（t，x）+g₁（t，x）y.若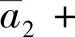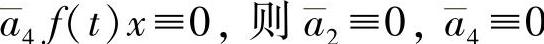，但由引理的条件这是不可能的.从而引理得证.

引理5.1.3 若F₁（t，x，y）=x，a₅（t）≠0，如果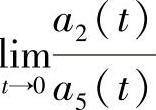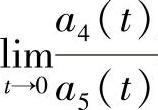，存在，则

证 若F₁（t，x，y）=x，则由式（5.1.3）推得

由此可推得该引理的结论.

定理5.1.1 若F₁（t，x，y）=f（t）x，a₅（t）≠0，且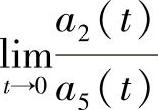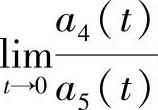，存在，则F₂（t，x，y）=g₀（t）+g₁（t）x+g₂（t）y.（其中g₀（t），g₁（t），g₂（t）为连续可微函数，t∈R）.

证 设F₁（t，x，y）=f（t）x，则由（5.1.3）得

对式（5.1.3）沿着式（5.3.1）的解求全导数得

由式（5.1.4）和式（5.1.5）计算得

这里

1）若B₂（t，x，y）≠0，则由式（5.1.6）得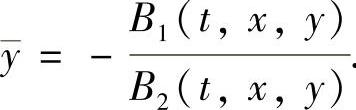由此及式（5.1.3）可推得

由上式得

将此式代入式（5.1.3）得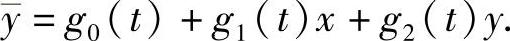在这种情况下定理得证.

2）若B₂（t，x，y）≡0，则B₁（t，x，y）≡0.当b₅≠0，由B₂（t，x，y）≡0，B₁（t，x，y）≡0推得f（t）=1和

其中α∶=a₅′+2a₅b₂-a₂b₅；β∶=2a₅b₄-a₄b_5.

由定理的条件及式（5.1.12）和式（5.1.13）推得a₂=m（t）a₅，a₄=n（t）a₅.由式（5.1.10）得a₅=γ（t）e^δ（t），这里

γ（t）+γ（-t）=0，

由式（5.1.7）和式（5.1.8）得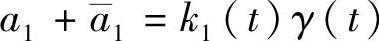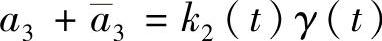，，其中k₁（t）+k₁（-t）=0，k₂（t）+k₂（-t）=0.

令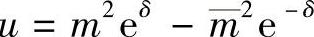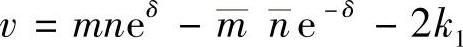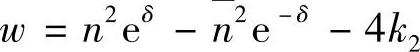；；；则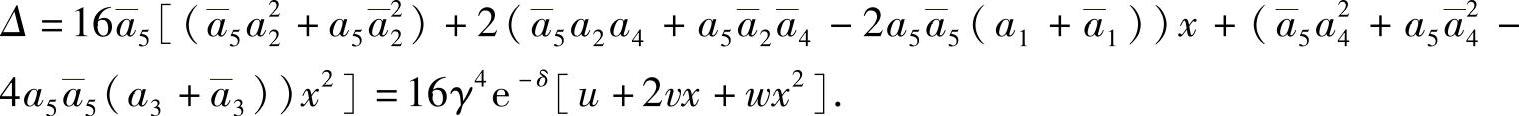

由引理5.1.3得u（0）=v（0）=w（0）=0.由式（5.1.7）～式（5.1.15）计算得

这是个齐线性方程组，由解的唯一性得u（t）=v（t）=w（t）≡0，从而Δ≡0.则由式（5.1.3）推得

当b₂≡0时，可类似讨论.定理得证.

定理5.1.2 若a₅（t）≠0，则1°若a₂≠0且(www.daowen.com)

其中

c₁=a₁′+a²₁+a₂b₁，c₂=a₂′+a₂a₁+a₂b_2.

则

为微分系统（5.1.1）的反射函数.

2°若a₂≡0且

其中

则F（t，x，y）=（fx，g₁x+g₂y）^T为微分系统（5.1.1）的反射函数.

除此之外，若微分系统（5.1.1）为2ω-周期系统，则该系统在[-ω，ω]有定义的解x=x（t，-ω，x₀，y₀），y=y（t，-ω，x₀，y₀）是2ω-周期解，当且仅当，F（-ω，x₀，y₀）=（x₀，y₀）^T.

证 当a₂≠0，由条件（5.1.16）得

由条件（5.1.2）得

从而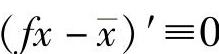，由f（0）=1得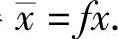由于F（0，x，y）=（x，y）^T及

这里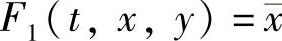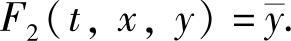，即在a₂≠0时，定理得证.在a₂≡0时，同理可证.其余结论由第2章基本引理2.1.2可得.

例5.1.1 微分系统

（a_i，b_i，i=1，2，3，4连续可微的奇函数t∈R），具有反射函数F（t，x，y）=（x，e^2sinty）^T.若a_i（t+2π）=a_i（t），b_i（t+2π）=b_i（t），i=1，2，3，4则该系统在[-π，π]上有定义的解都是2π-周期函数.

当a₅≡0和a₄≠0时同理可得下面的结论：

定理5.1.3 若a₅≡0及a₄≠0，则1°若a₂≠0及

或

其中，，，，，，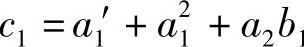

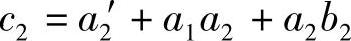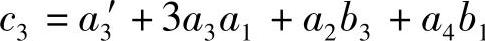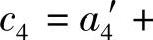
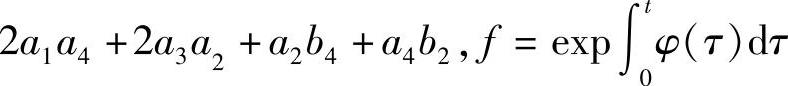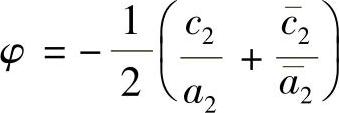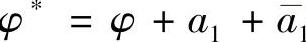则

为微分系统（5.1.1）的反射函数.

2°若a₂≡0及

其中

则F（t，x，y）=（fx，g₁x+g₂y）^T为微分系统（5.1.1）的反射函数.除此之外，若微分系统（5.1.1）为2ω-周期系统，则该系统在[-ω，ω]有定义的解x=x（t；-ω，x₀，y₀），y=y（t；-ω，x₀，y₀）是2ω-周期解，当且仅当F（-ω，x₀，y₀）=（x₀，y₀）^T.

例5.1.2 微分系统

具有非线性反射函数

这里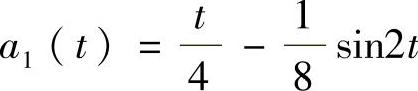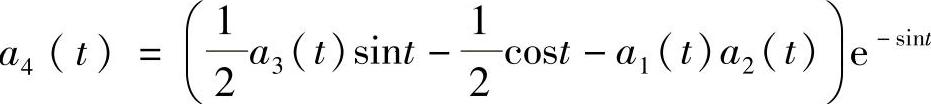，，a₂（t），a₃（t）为任意连续可微的奇函数.

定理5.1.4 若a₅=a₄≡0及a₂≠0及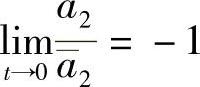，则1°若b₅≡0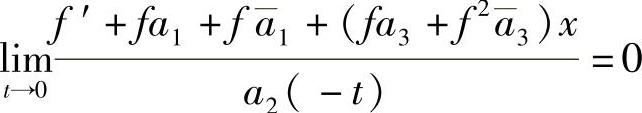，及

（函数c₁，c₂，f，φ的定义与定理5.1.3中相同），则

为微分系统（5.1.1）的反射函数.2°若b₅≠0及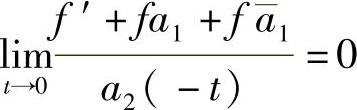及

（函数c₁，c₂，f，φ，φ^∗的定义与定理5.1.3中相同），则

为微分系统（5.1.1）的反射函数.除此之外，若微分系统（5.1.1）为2ω-周期系统，则该系统在[-ω，ω]上有定义的解x=x（t；-ω，x₀，y₀），y=y（t；-ω，x₀，y₀）为2ω-周期解，当且仅当，F（-ω，x₀，y₀）=（x₀，y₀）^T.

例5.1.3 微分系统

具有反射函数F（t，x，y）=（x，e^2sinty+（e^2sint-1）x²）T，这里α（t）+α（-t）=0，β（t）+β（-t）=0且连续可微.若α（t+2π）=α（t），β（t+2π）=β（t）.则该微分系统在[-π，π]上有定义的解皆是2π-周期解.

显然，对于微分系统（5.1.1），当a₂=a₄=a₄=0及f′+fa₁+fa₁=0，a₃+a₃f=0，那该系统反射函数的第一分量具有形式x=f（t）x.