现在我们考虑二阶微分方程
x″=a00(t)+a10(t)x+a01(t)x′+a20(t)x2+a11(t)xx′+a02(t)x′2, (4.3.1)
这里aij(t)在R上连续可微,(i,j=0,1,2)
Riccati方程
u′=α0(t)+α1(t)u+α2(t)u2, (4.3.2)
其中αi(t)在R上连续可微,(i,j=0,1,2)且α2(t)≠0.
设x(t)为方程(4.3.1)的任一解,构造函数
u(t)=b00(t)+b10(t)x(t)+b01(t)x′(t), (4.3.3)
bij(t)在R上连续可微,(i,j=0,1).
从4.4.1知,我们可以通过反射函数的性质来研究Riccati方程(4.3.2)周期解的个数及稳定性态.下面我们将应用Riccati方程(4.3.2)周期解的性态来研究微分方程(4.3.1)的性态.
引理 4.3.1 假设a02(t)a11(t)≠0,对于方程(4.3.1)存在连续可微函数α0(t),α1(t),α2(t)(α2≠0)和b00(t),b01(t),b10(t)满足:
a211(t)=4a20(t)a02(t),δ′=δ2+a01(t)δ-a10,
b0′0(t)+b01(t)a00(t)=α0(t)+α1(t)b00(t)+α2(t)b200(t).
则u(t)为Riccati方程(4.3.2)的解.
其中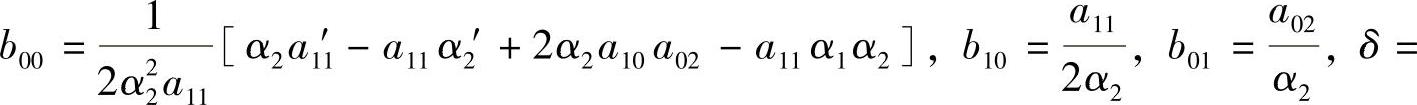
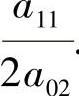
证 由于x(t)为方程(4.3.1)的任一解,则
比较上式两边x(t),x′(t)同次幂的系数得
b0′0+b01a00=α0+α1b00+α2b200,
b1′0+b01a10=α1b10+2α2b00b10,
b0′1+b10+a01b01=α1b01+2α2b00b01,
b01a20=α2b210, a11=2α2b10,
b01a02=α2b201.
由上式不难计算可得引理的结论成立.
在引理的条件下,方程(4.3.1)可表示成
x″=a00+(δ2-δ′)x+a01(δx+x′)+a02(δx+x′)2.
式(4.3.3)变为
u(t)=b00+b01(δx(t)+x′(t)).
若取b00=0,b01=1,则方程(4.3.1)变为
u′=a00+(a10+δ)u+a02u2.
定理4.3.1 假设引理4.3.1的条件满足,且方程(4.3.1)和方程(4.3.2)的系数函数均为连续的2ω-周期函数,则
1)若Riccati方程(4.3.2)没有2ω-周期解,则方程(4.3.1)没有2ω-周期解;
2)若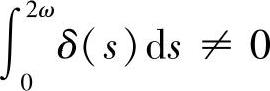 ,并且方程(4.3.2)有且仅有一个2ω-周期解,则方程(4.3.1)最多只有一个2ω-周期解;
,并且方程(4.3.2)有且仅有一个2ω-周期解,则方程(4.3.1)最多只有一个2ω-周期解;
3)若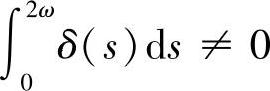 ,并且方程(4.3.2)有且仅有两个2ω-周期解,则方程(4.3.1)最多只有两个2ω-周期解.
,并且方程(4.3.2)有且仅有两个2ω-周期解,则方程(4.3.1)最多只有两个2ω-周期解.
证 1)反证 若方程(4.3.1)有一个2ω-周期解x(t),则u(t)=b00(t)+b01(t)(δ(t)x(t)+x′(t))为方程(4.3.2)的一个2ω-周期解,与假设矛盾,故结论1成立.
2)反证 若此时方程(4.3.1)存在两个2ω-周期解x1(t),x2(t),且x1(t)≠x2(t).则
u1(t)=b00+b01(δ(t)x1(t)+x1′(t)),
u2(t)=b00+b01(δ(t)x2(t)+x2′(t))
都是方程(4.3.2)的周期解,由假设得u1(t)≡u2(t),即
δ(t)(x1(t)-x2(t))+(x1(t)-x2(t))′=0,
解此方程得
因此有
由于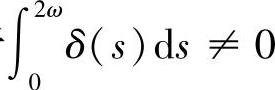 ,则x1(t)≡x2(t).与假设矛盾.故结论2成立.与2)同理可证结论3)成立.
,则x1(t)≡x2(t).与假设矛盾.故结论2成立.与2)同理可证结论3)成立.
引理4.3.2 对于可微函数x(t)和2ω-周期函数δ(t),若
则
其中σ(t)是一个2ω-周期函数.
证 令
由于
又由式(4.3.4)得
x′(t+2ω)-x′(t)=-δ(t)(x(t+2ω)-x(t)),则σ(t+2ω)=σ(t).即σ(t)为2ω-周期函数.又
解此一阶微分方程即得关系式(4.3.5).
引理4.3.3 对可微函数x(t)和2ω-周期函数δ(t),若式(4.3.4)成立,则当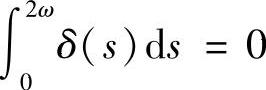 时,有
时,有
这里σ(t)和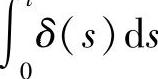 都是2ω-周期函数.
都是2ω-周期函数.
证记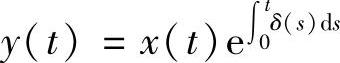 ,则x(0)=y(0),x(2ω)=y(2ω).又
,则x(0)=y(0),x(2ω)=y(2ω).又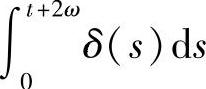
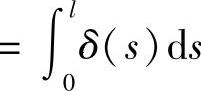 ,则由式(4.3.4)得
,则由式(4.3.4)得
y(t+2ω)-y(t)=x(2ω)-x(0).
微分此恒等式得
y′(t+2ω)-y′(t)=0.
即y′(t)为2ω-周期函数,则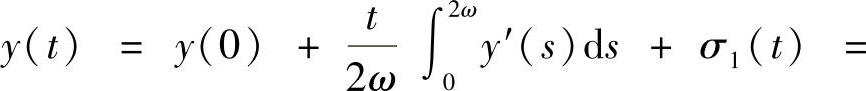
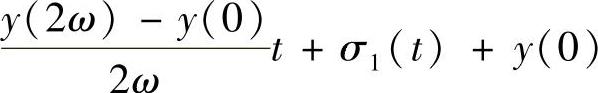 ,这里σ1(t)为2ω-周期函数[4].因此只要取σ(t)=σ1(t)+y(0),即得式(4.3.6)成立.
,这里σ1(t)为2ω-周期函数[4].因此只要取σ(t)=σ1(t)+y(0),即得式(4.3.6)成立.
定理4.3.2 假设引理4.3.1的条件满足,方程(4.3.1)和方程(4.3.2)所有系数都是2ω-周期函数,并且方程(4.3.2)的所有解都是2ω-周期解,则对于方程(4.3.1)的任一解x(t)
1)若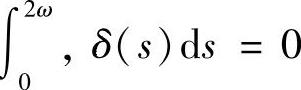 ,则
,则
这里σ(t)和∫0tδ(s)ds都是2ω-周期函数,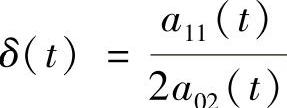 ;
;
2)若x(2ω)=x(0),则x(t)为2ω-周期函数;
3)若x(2ω)≠x(0),则当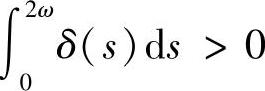 时,
时,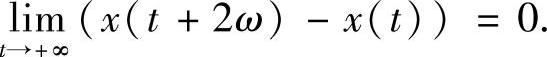 当
当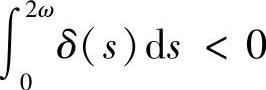 时,
时,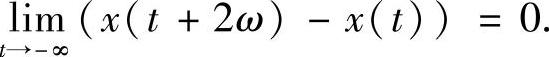
证 设x(t)为方程(4.3.1)的任一解,则u(t)=b00(t)+b01(t)(δ(t)x(t)+x′(t))为式(4.3.2)的解,且u(t+2ω)=u(t),即
δ(t)(x(t+2ω)-x(t))+(x(t+2ω)-x(t))′=0.
解此方程得
由此可得,若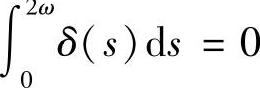 ,由引理4.3.3得结论1)成立.若x(2ω)=x(0),则x(t+2ω)=x(t),即结论2)成立.若x(2ω)≠x(0),由于
,由引理4.3.3得结论1)成立.若x(2ω)=x(0),则x(t+2ω)=x(t),即结论2)成立.若x(2ω)≠x(0),由于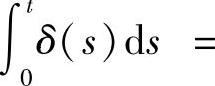
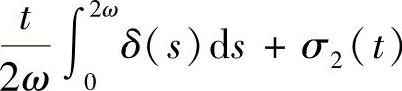 ,σ2(t)一个2ω-周期函数[4],则有
,σ2(t)一个2ω-周期函数[4],则有
由于σ2(t)为2ω-周期函数,从而有界.则由上面关系式即可得结论3)成立.
我们可以利用上述方法来讨论微分方程
当aij(t+2ω)=aij(t)(i,j=0,1,2,…),其周期解的个数.
根据引理4.3.1我们不妨考虑二阶微分方程
其中ai(t),δ(t),a1∗(t)为连续可微函数(i=0,1,2,3,…,n).
对其任一解x(t),构造函数
记y=δx+x′,则式(4.3.7)和式(4.3.8)变为
其中a1(t)=a1∗(t)+δ(t).
下面将建立Riccati方程(4.3.2)与方程(4.3.7)解之间的关系?
定理4.3.3 设an≠0,对微分方程(4.3.9)存在连续可微函数α0,α1,α2(α2≠0)和bi(i=0,1,2,…,n-1)若(www.daowen.com)
则函数(4.3.10)为Riccati方程(4.3.2)的解.其中
若k>n,ak=0,若k>n-1,bk=0.
证 由定理的条件得
比较等式两边y的同次幂的系数得
其中ak=0,当k>n时.bk=0,当k>n-1时.
计算式(4.3.14)即可推得式(4.3.12).由式(4.3.13)和计算bk′bn-1-b′n-1bk(k=1,2,…,n-2)可得式(4.3.11)成立.
综上即可得定理的结论成立.
例4.3.1 考虑微分方程
对其任一解x(t),函数
满足Riccati方程
下面我们总假设定理4.3.3的条件满足,并且微分方程(4.3.2),方程(4.3.7)和方程(4.3.8)的所有系数为t的2ω-周期函数.
定理4.3.4 若Riccati方程(4.3.2)没有2ω-周期解,则方程(4.3.6)也没有2ω-周期解.
证 反证 若方程(4.3.7)有一个2ω-周期解,则函数
为方程(4.3.2)的2ω-周期解,这与定理的假设矛盾.从而定理的结论成立.
推论4.3.1 若α1(t)+α1(-t)=0,α0(t)=α0(-t),α2(t)=α2(-t),α2(t)≥0,α0(t)≥0或α0(t)≤0,α2(t)≤0,t∈R,且存在τ∈R使得α2(τ)α0(τ)>0,则方程(4.3.7)没有2ω-周期解.
由定理4.1.3知,此时微分方程(4.3.2)不存在2ω-周期解,则由定理4.3.4得推论的结论成立.
推论4.3.2 若α21<4α0α1,则方程(4.3.7)没有2ω-周期解.
该结论可由推论4.1.1及定理4.3.4得.
定理4.3.5 若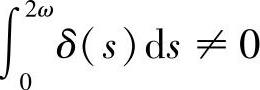 及Riccati方程(4.3.2)仅有一个2ω-周期解,则方程(4.3.7)最多具有n-1个2ω-周期解.
及Riccati方程(4.3.2)仅有一个2ω-周期解,则方程(4.3.7)最多具有n-1个2ω-周期解.
证 反证 假设方程(4.3.7)具有n个2ω-周期解xi(t)(i=1,2,…,n)且xi(t)≠xj(t)(i,j=1,2,…,n,i≠j).则yi(t)=δ(t)xi(t)+xi′(t)(i=1,2,…,n)都是方程(4.3.8)的2ω-周期解.下面证明存在i,j(1≤i≠j≤n)使得
yi(t)≡yj(t). (4.3.15)
假设对任意的i,j(1≤i≠j≤n),都有
yi(t)-yj(t)≠0. (4.3.16)由式(4.3.10)得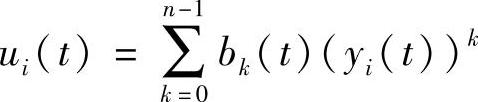 (i=1,2,…,n)都是方程(4.3.2)的2ω-周期解.由定理的条件得
(i=1,2,…,n)都是方程(4.3.2)的2ω-周期解.由定理的条件得
ui(t)≡uj(t) (i,j=1,2,…,n), (4.3.17)
则
ui(t)-uj(t)≡0 (i,j=1,2,…,n),
即
由于y1-yj≠0,则
即
将上面其他式减去第一式得
又由于y2-yj≠0,则
重复上述步骤得
即
两式相减得
bn-1(yn-1-yn)≡0.
又由于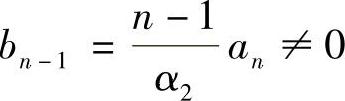 ,则yn-1-yn≡0,这与式(4.3.16)矛盾.因此式(4.3.15)成立,即
,则yn-1-yn≡0,这与式(4.3.16)矛盾.因此式(4.3.15)成立,即
δ(t)(xi(t)-xj(t))+(xi(t)-xj(t))′≡0 (i≠j),
解此方程得
又因为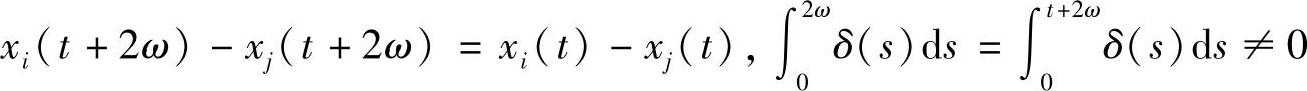 ,则xi(0)-xj(0)=0,从而xi(t)-xj(t)≡0,这与假设矛盾,从而定理得证.
,则xi(0)-xj(0)=0,从而xi(t)-xj(t)≡0,这与假设矛盾,从而定理得证.
定理4.3.6假设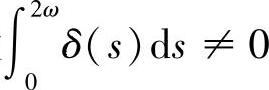 及Riccati方程(4.3.2)恰有两个2ω-周期解,则方程(4.3.7)至多有n个2ω-周期解.
及Riccati方程(4.3.2)恰有两个2ω-周期解,则方程(4.3.7)至多有n个2ω-周期解.
证 反证 若方程(4.3.7)有n+1个2ω-周期解xi(t)(i=1,2,…,n+1)且xi(t)≠xj(t)(i≠j),则yi(t)=δ(t)xi(t)+xi′(t)(i=1,2,…,n+1)是方程(4.3.9)的2ω-周期解,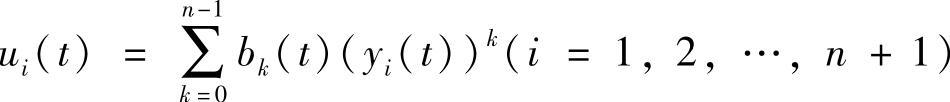 都是Riccati方程(4.3.2)的2ω-周期解.根据定理的假设与定理4.3.5同理可证定理4.3.6的结论成立.
都是Riccati方程(4.3.2)的2ω-周期解.根据定理的假设与定理4.3.5同理可证定理4.3.6的结论成立.
推论4.3.3 若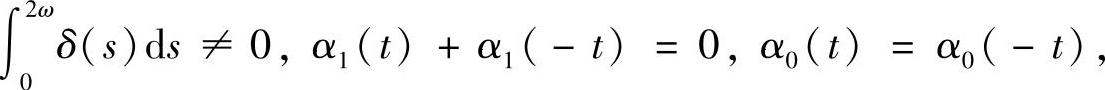
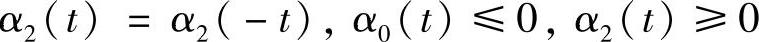 ,并且存在τ∈R使得α2(τ)α0(τ)<0,方程(4.3.2)至少有一个解在[-ω,ω]上有定义,则方程(4.3.7)至多存在n个2ω-周期解.
,并且存在τ∈R使得α2(τ)α0(τ)<0,方程(4.3.2)至少有一个解在[-ω,ω]上有定义,则方程(4.3.7)至多存在n个2ω-周期解.
在上述条件下,再由定理4.1.2知,此时Riccati方程(4.3.2)恰有两个2ω-周期解,再应用定理4.3.6的结论即可推得推论4.3.3
下面我们记
λij=x(2iω)-x(2jω), μij=x(t+2iω)-x(t+2jω), 0≤i≠j≤n-1.
定理4.3.7 假设Riccati方程(4.3.2)的所有解皆为2ω-周期解.则对方程(4.3.7)的任一解x(t),1)若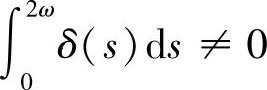 ,则存在i,j,0≤i≠j≤n-1,使得
,则存在i,j,0≤i≠j≤n-1,使得
其中m(t)是一个2(j-i)ω-周期函数;
2)若对上面i,j,λij=0,则x(t+2iω)是t的2(j-i)ω-周期函数;
3)若对上面i,j,λij≠0,则当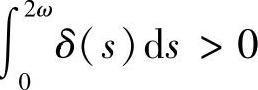 ,
,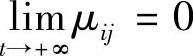 ;当
;当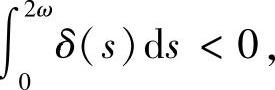
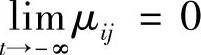 ;4)若
;4)若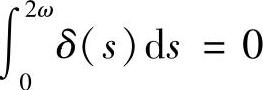 ,
,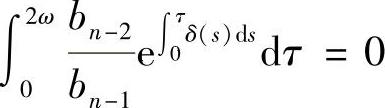 ,
,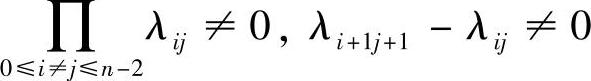 ,(0≤i≠j≤n-2),λ0n=0,则x(t)为2(n-1)ω-周期函数;5)若∫
,(0≤i≠j≤n-2),λ0n=0,则x(t)为2(n-1)ω-周期函数;5)若∫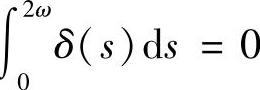 ,
,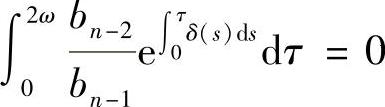 ,
,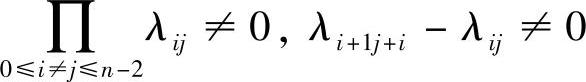 ,(1≤i≠j≤n-1),λ1n=0,则x(t)为2nω-周期函数.
,(1≤i≠j≤n-1),λ1n=0,则x(t)为2nω-周期函数.
证 设x(t)为式(4.3.7)的任一解.记yi(t)=δ(t)x(t+2iω)+x′(t+2iω),(i=1,2,…,n-1),则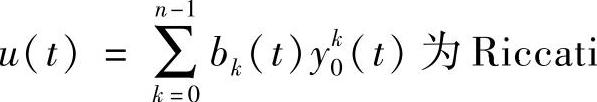 方程(4.3.2)的2ω-周期解,则
方程(4.3.2)的2ω-周期解,则
u(t)=u(t+2ω)=…=u(t+2(n-1)ω),
即
应用此式,与定理4.3.5同理可得,存在i,j,0≤i≠j≤n-1使得
yi(t)=yj(t),
即
δ(t)(x(t+2iω)-x(t+2jω))+(x(t+2iω)-x(t+2jω))′=0,由此得
因此,与定理4.3.2和引理4.3.3类似可证得定理的前三个结论成立.
下面验证结论4成立.
先证在条件4)成立时,有yi(t)≠yj(t)(0≤i≠j≤n-2).
反证 若存在i,j,(0≤i≠j≤n-2)使得
yi(t)=yj(t),
则
由此得
x(2(i+1)ω)-x(2(j+1)ω)=x(2iω)-x(2jω),
即
λi+1j+1=λij.
这与定理的条件4)矛盾.因此由式(4.3.18)可推得
bn-2+bn-1(y0+y1+…+yn-3+yn-2)=0.
解此方程得
应用条件4)得
因此
x(t)=x(t+2(n-1)ω).
从而定理的结论4)成立.同理可证结论5)成立.综上,定理得证.
推论4.3.4 若αi(t)+αi(-t)=0(i=0,1,2),则定理4.3.7的结论成立.
由本章4.1知,此时Riccati方程的反射函数为F(t,u)=u,从而该方程的所有解均为2ω-周期函数,则由定理4.3.7得推论成立.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。