一个微分方程具有形如的反射函数

本节我们主要讨论何时一个微分方程具有形如

F（t，x）=M（t）x+N（t）， （t，x）∈R² （4.2.1）

的反射函数.

引理4.2.1 函数（4.2.1）为某个微分方程的反射函数，当且仅当

F（t，x）=xe^2m（t）+n（t）e^m（t）. （4.2.2）

其中m（t），n（t）为奇的可微函数.

证 必要性 设F（t，x）=M（t）x+N（t）为某个微分方程的反射函数，则由反射函数的性质2）得

M（-t）[M（t）x+N（t）]+N（-t）=x，

即

M（-t）M（t）=1，M（-t）N（t）+N（-t）=0. （4.2.3）

由F（0，x）=x得M（0）=1，N（0）=0.从而有M（t）＞0.令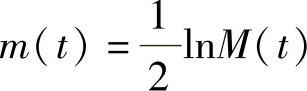，则M（t）=e^2m（t）.又由M（-t）M（t）=1得，m（t）+m（-t）=0，即m（t）为奇函数.又由式（4.2.3）得e^2m（-t）N（t）+N^（-t）=0.令N（t）e^-m（t）=n（t），则n（t）+n（-t）=0，N（t）=n（t）e^m（t），从而有F（t，x）=xe^2m（t）+n（t）e^m（t）.

充分性 由于F（t，x）=xe^2m（t）+n（t）e^m（t），则

F（-t，F（t，x））=F（0，x）=x.

显然该函数为方程

的反射函数.

推论4.2.1 函数F（t，x）=x+n（t）为某个微分方程的反射函数，当且仅当，n（t）为奇函数.

证F（t，x）=x+n（t）为某个微分方程的反射函数，当且仅当，F（-t，F（t，x））=F（0，x）=x，即n（t）+n（-t）=0.

定理4.2.1 具有连续可微右端函数的微分方程以式（4.2.2）为反射函数，当且仅当，该微分方程可以表示成

这里R（t，x）为任意连续可微函数.

该结论可与第2章定理2.2.2同理可得.

在该定理中取m（t）≡0，则得：

推论4.2.2 具有连续可微右端函数的微分方程以F（t，x）=x+n（t）为反射函数，当且仅当，该微分方程可以表示成

这里R（t，x）为任意连续可微函数.

定理4.2.2 假设

1）方程（4.2.5）的右端为t的2ω-周期函数；

2）m（t），n（t）为连续可微的奇函数；

3）R（t，x）在R²上连续可微；

4）方程（4.2.5）的解在[-ω，ω]上有定义，

则

i）当m（ω）≠0时，方程（4.2.5）具有唯一2ω-周期解，且该周期解，当m（ω）＞0时渐近稳定，当m（ω）＜0时不稳定；

ii）当m（ω）=n（ω）=0时，方程（4.2.5）的一切解皆是2ω-周期解；

iii）当m（ω）=0，n（ω）≠0时，方程（4.2.5）不存在2ω-周期解.

证 设方程（4.2.5）的反射函数为（4.2.2），则其Poincaré映射为

T（x）=F（-ω，x）=xe^2m（-ω）+n（-ω）e^m（-ω）

=xe^-2m（ω）-n（ω）e^-m（ω）.

由此及第2章的基本引理2.1.1即得该定理的结论.

例4.2.1 微分方程

具有形如式（4.2.2）的反射函数，当且仅当，

b（t）+b（-t）cosα（t）+c（-t）sinα（t）≡0；

c（t）-b（-t）sinα（t）+c（-t）cosα（t）≡0.

这里

并且此时，该微分方程的反射函数为F（t，x）=x+α（t）.若方程（4.2.6）中a（t），b（t），c（t）为2ω-周期连续可微函数.则当α（ω）=0时，方程（4.2.6）所有在[-ω，ω]上有意义的解皆为2ω-周期解.当α（ω）≠0时，方程（4.2.6）不存在2ω-周期解.

例4.2.2 微分方程

具有反射函数F（t，x）=x+α（t）.其中a（t）为任意偶函数，α（t）为任意奇函数，b（t）为任意连续函数.

下面我们来讨论一阶微分方程

这里X（t，x）在R²上连续关于x解析.

问题：方程（4.2.7）何时其反射函数为线性的？若是线性的，那如何寻找该线性反射函数？

根据反射函数的性质，我们知道式（4.2.1）为系统（4.2.7）的反射函数，当且仅当

M′（t）x+N′（t）+M（t）X（t，x）+X（-t，M（t）x+N（t））≡0，(https://www.daowen.com)

M（0）=1，N（0）=0. （4.2.8）由于X（t，x）关于x解析，从而关于x可任意阶求导，则有

N′（t）+M（t）X（t，0）+X（-t，N（t））≡0； （4.2.9）

M′（t）+M（t）X^（1）（t，0）+M（t）X^（1）（-t，N（t））≡0； （4.2.10）

M（t）X^（i）（t，0）+M^（i）（t）X^（i）（-t，N（t））≡0（i=2，3，…） （4.2.11）

这里X^（i）为X（t，x）关于x的i阶偏导数.

因此，式（4.2.1）为微分系统（4.2.7）的反射函数的充要条件是式（4.2.9）～式（4.2.11）同时成立.

若方程（4.2.7）为线性方程时，我们可以求出其通解，从而其反射函数F（t，x）=φ（-t；t，x）.若方程（4.2.7）不是线性方程时，方程（4.2.11）中至少有一个不是恒等式，从而由式（4.2.9）～式（4.2.11）可以解出M（t），N（t），从而F（t，x）就可以求出.

现在我们考虑Riccati方程

这里a（t），b（t），c（t）连续可微，t∈R.

对于Riccati方程，方程（4.2.9）～方程（4.2.11）变为

N′+Ma（t）+a（-t）+b（-t）N+c（-t）N²≡0； （4.2.13）

M′+M[b（t）+b（-t）+2c（-t）N（t）]≡0； （4.2.14）

2Mc（t）+2M²c（-t）≡0. （4.2.15）

由式（4.2.15）得M（t）=e^2m（t），c（t）+c（-t）e^2m（t）≡0.令r（t）=c（t）e^-m（t），则r（t）+r（t）≡0，从而r²（t）≡-r（t）r（-t）≡-c（t）c（-t），因此c（t）c（-t）≤0，

则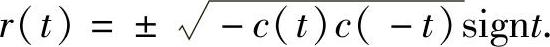

又由r（t）=c（t）e^-m（t）得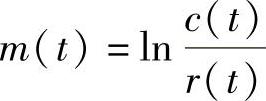，则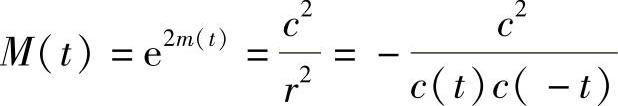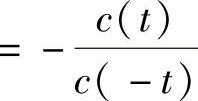.将此代入式（4.2.13）和式（4.2.14）后解出N（t），从而F（t，x）的表达式就有了.

现在我们来看看Riccati方程（4.2.12）具有形如F（t，x）=M（t）x的反射函数的条件.

定理4.2.3F（t，x）=M（t）x为Riccati方程（4.2.12）的反射函数，当且仅当，函数

为t的奇函数.此时

证 必要性 设F（t，x）=M（t）x为方程（4.2.12）的反射函数，则

由上第二式得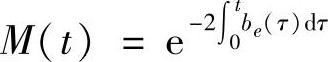，将此式代入上面其他两式得

因此必要性得证.

充分性 在条件（4.2.16）成立时，可直接验证（4.2.12）的反射函数.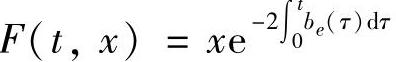为方程

定理4.2.4 假设函数（4.2.16）为奇函数，方程（4.2.12）的系数函数为连续的2ω-周期函数，且方程（4.2.12）的解φ（t；-ω，0）在[-ω，ω]上有意义，则

1）当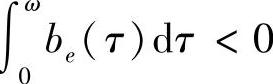时，方程（4.2.12）有唯一2ω-周期解φ（t；-ω，0）且稳定；

2）当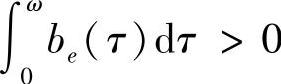时，方程（4.2.12）的唯一2ω-周期解不稳定；3）当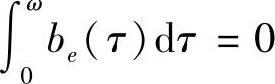时，方程（4.2.12）在[-ω，ω]上有意义的解均为2ω-周期解.

证 由定理4.2.3得，方程（4.2.12）的Poincaré映射

由此即可得上述结论.

现在我们来讨论微分方程

这里a_i（t）在R上连续（i=0，1，2，…，l）.由于上式右端为x的解析函数，则关系式（4.2.9）～式（4.2.11）等价于

当k=l-1，k=l时式（4.2.20）变为

Ma_l-1（t）+M^l-1[a_l-1（-t）+la_l（-t）N]=0； （4.2.21）

Ma_l（t）+M^la_l（-t）=0. （4.2.22）

又由引理4.2.1得M=e^2m（t），N=n（t）e^m（t），m（t），n（t）为奇函数.将此代入式（4.2.21）和式（4.2.22）得

a_l-1（t）+e²（l^-2）^m（t）[a_l-1（-t）+la_l（-t）n（t）e^m（t）]=0； （4.2.23）

a_l（t）+a_l（-t）e^{2（l-1）m（t）}=0. （4.2.24）

不失一般性，令

a_l（t）=α（t）e^{（l-1）m（t）}. （4.2.25）

将此代入式（4.2.24）得α（t）+α（-t）≡0，由此及式（4.2.25）得

α²（t）=-α（t）α（-t）=-a_l（t）e^{（1-l）m（t）}a_l（-t）e^{（1-l）m（-t）}

=-a_l（t）a_l（-t），

则

由此，我们可以假设a_l（t）a_l（-t）≤0，且具有式（4.2.25）形式，其中α（t）为连续的奇函数.则由式（4.2.25）得

又由式（4.2.23）得

la_l（-t）n（t）e^m（t）=-a_l-1（t）e^{2（2-l）m（t）}-a_l-1（-t），

从而

因此，F（t，x）=e^2m（t）x+n（t）e^m（t）就可用方程（4.2.17）的系数来表示.再验证反射函数的基本关系式，即可推得a_i（t）（i=0，1，2，…，l）所应满足关系式，这样就回答了何时微分方程（4.2.17）具有F（t，x）=e^2m（t）x+n（t）e^m（t）形式的反射函数.

对于微分系统（n＞1），何时具有F（t，x）=M（t）x+N（t）的反射函数？可以类似推得.