考虑Riccati方程

其中a（t），b（t），c（t）为R上的连续函数.

记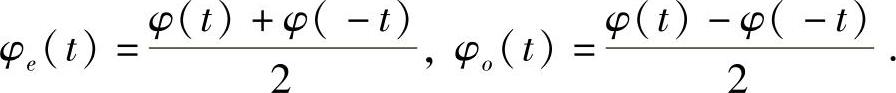

引理4.1.1 微分方程（4.1.1）具有如下形式的反射函数

若r（t），s（t），n（t），z（t）为线性微分系统：

满足初始条件

r（0）=s（0）=n（0）=0，z（0）=1 （4.1.4）

的解，并且r（t），s（t），n（t）为奇函数，z（t）为偶函数，m（t）=z（t）+n（t）.在反射函数定义域内存在子集，使得m（-t）+s（t）x＞0成立.

证 记

y₁（t）=r（t）+r（-t）；y₂（t）=s（t）+s（-t）；

y₃（t）=n（t）+n（-t）；y₄（t）=z（t）-z（-t）.

则

y₁′（t）=r′（t）-r′（-t）=b_oy₁-2a_oy₃-2a_ey₄；

y₂′（t）=s′（t）-s′（-t）=-b_oy₂-2c_oy₃+2c_ey₄；

y₃′（t）=n′（t）-n′（-t）=c_oy₁+a_oy₂-b_ey₄；

y₄′（t）=z′（t）+z′（-t）=c_ey₁-a_ey₂-b_ey₃；

y₁（0）=y₂（0）=y₃（0）=y₄（0）=0.

由齐线性微分方程组解的唯一性得

y₁（t）≡y₂（t）≡y₃（t）≡y₄（t）≡0.

从而式（4.1.3）满足式（4.1.4）的解r（t），s（t），n（t）为奇函数，z（t）为偶函数.

下面验证式（4.1.2）确实是系统（4.1.1）的反射函数.为了证明方便起见，式（4.1.1）可以改写成

由此及式（4.1.3）易验证

故F（t，x）为系统（4.1.1）的反射函数.

下面说明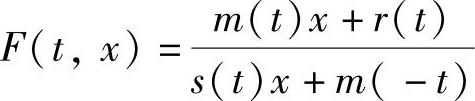对∀（t，x）都有意义，即不存在τ∈R，使得s（τ）=m（-τ）=0.事实上，由式（4.1.3）可计算得z²（t）-n²（t）-r（t）s（t）=c为其首次积分，再由初始条件得z²（t）-n²（t）-r（t）s（t）≡1，即m（t）m（-t）-r（t）s（t）≡1，由此可知，m（t）与s（t）不可能有共同的零点.又当t=0时，m（0）+s（0）x=1＞0，由此即得定理的结论成立.

注4.1.1 若方程（4.1.1）至少有一个解在[-α，α]上有意义，且s（α）≠0，则对所有满足m（α）-s（α）x＞0的x，方程（4.1.1）的解φ（t；-α，x）在[-α，α]上有意义.

事实上，考虑方程（4.1.1）的解族φ（t；-α，x），x∈R，设从（-α，x₀）出发的解φ（t；-α，x₀）在[-α，α]上有意义.若存在x^∗，m（α）-s（α）x^∗＞0，方程过（-α，x^∗）的解φ（t；-α，x^∗）在t=α时不存在，且对∀x，|x-x₀|＜|x^∗-x₀|，φ（t；-α，x）在[-α，α]上有意义，则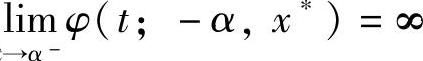（由第1章定理1.1.3），则由反射函数的性质得

由此得m（α）-s（α）x^∗=0，与假设矛盾.

注4.1.2 关系式z²-n²-rs=c为微分系统（4.1.3）的一个首次积分，则对反射函数（4.1.2）有m（t）m（-t）-r（t）s（t）≡1，从而该分式函数是不可约的.

注4.1.3 对任意连续可微的奇函数r（t），s（t），n（t）和连续可微的奇函数a_o（t），b_o（t），c_o（t）.令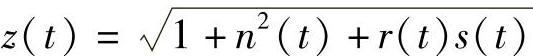，则由系统（4.1.3）可以唯一确定a_e（t），b_e（t）和c_e（t），从而可以构造所有以（4.1.2）为反射函数的Riccati方程.

定理4.1.1 设a（t），b（t），c（t）为R上的连续2ω-周期函数，r（t），s（t），n（t），z（t）为微分系统（4.1.3）满足初值（4.1.4）的解，则微分方程（4.1.1）的Poincaré映射为

其中m（ω）-s（ω）x＞0.微分方程（4.1.1）在[-ω，ω]上有意义的解x（t）为2ω-周期，当且仅当，λ=x（ω）为代数方程

s（ω）λ²-2n（ω）λ-r（ω）=0 （4.1.6）

的解.

当s（ω）≠0时，x（t）为2ω-周期解，当且仅当，λ=x（ω）为方程（4.1.6）的解，且m（ω）-s（ω）λ＞0.

证 由引理4.1.1及第2章基本引理2.1.1可推得定理的第一部分结论.

当s（ω）≠0，m（ω）-s（ω）λ＞0，则由注4.1.1得x（t），x（-ω）=λ，在[-ω，ω]上有意义，从而它为2ω-周期解的充要条件为λ为方程（4.1.6）的解.

推论4.1.1 若方程（4.1.1）中a（t），b（t），c（t）为连续的2ω-周期函数，则下列结论之一成立：

1）方程（4.1.1）不存在2ω-周期解；

2）方程（4.1.1）仅有一个2ω-周期解；

3）方程（4.1.1）恰有两个2ω-周期解；

4）方程（4.1.1）在[-ω，ω]上有意义的解皆为2ω-周期解.

该结论可由定理4.1.1的结论及代数方程（4.1.6）的根的不同情况所得.下面四个Riccati方程可说明上述推论中的各种情形.

（1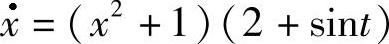）没有2π-周期解.(www.daowen.com)

（2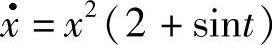）存在唯一2π-周期解.

（3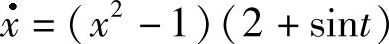）存在两个2π-周期解.

（4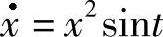）所有解皆为2π-周期解.

在参考文献[17]中已证明对于方程（4.1.1），当c（t）≠0时，该方程不可能有多于两个周期解.

应用定理4.1.1我们还可以推出更多的结论.

定理4.1.2 假设

1）方程（4.1.1）的系数函数a（t），b（t），c（t）为连续的2ω-周期函数；

2）b（t）+b（-t）=0，a（t）=a（-t），c（t）=c（-t）；

3）对∀t∈R，a（t）≤0，c（t）≥0，且存在τ∈R，使得a（τ）c（τ）＜0；

4）方程（4.1.1）至少有一个解在[-ω，ω]上有意义.

则方程（4.1.1）恰有两个2ω-周期解.

证 在定理的条件下，微分系统（4.1.3）变为

n（t）≡0， s（0）=r（0）=0， z（0）=1.

由于a（t），c（t）为偶连续2ω-周期函数，因此只需在[0，ω]上考虑微分系统（4.1.7）.显然，z²（t）=1+r（t）s（t）为系统（4.1.7）的一个首次积分.又由条件a（t）≤0，c（t）≥0，且存在τ∈[0，ω]使得a（τ）c（τ）＜0.则由系统（4.1.7）得（r′-br）（s′+bs）=-4acz²≥0.又由z²=1+rs可得r（ω）＞0，s（ω）＞0，z（ω）＞0^[18].从而方程（4.1.6）变为s（ω）λ²-r（ω）=0，此时它恰有两个根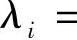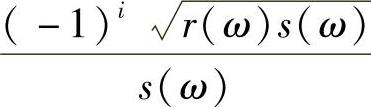，，且

由定理4.1.1得，方程（4.1.1）恰有两个2ω-周期解.

注4.1.4 若定理4.1.2中的条件3改为对∀t∈R，a（t）≥0，c（t）≤0，且∃τ∈R使得a（t）c（t）＜0成立，此时定理4.1.2的结论同样成立.

定理4.1.3 假设

1）方程（4.1.1）的系数函数a（t），b（t），c（t）为连续的2ω-周期函数；

2）b（t）+b（-t）=0，a（t）=a（-t），c（t）=c（-t）；

3）对∀t∈R，a（t）≥0，c（t）≥0（或a（t）≤0，c（t）≤0），并存在τ∈R，使得a（t）c（t）＞0，则方程（4.1.1）不存在2ω-周期解.

证 对方程（4.1.1）作变换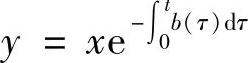，则方程（4.1.1）变为

由于b（t）+b（-t）=0，则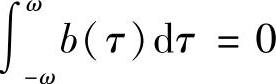，从而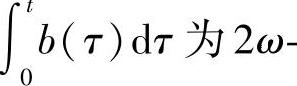周期函数.因此方程（4.1.1）的2ω-周期解与方程方程（4.1.8）的周期解一一对应.又由于方程（4.1.8）的右端函数为定号函数，从而方程（4.1.8）的解为单调函数，则它不可能为周期函数，因此方程（4.1.1）不存在2ω-周期解.

定理4.1.4 设方程（4.1.1）中a（t），b（t），c（t）为2ω-周期函数，对某有限数α＞0，c（-t）≡-αa（t），b（-t）≡b（t），方程（4.1.1）的解φ（t；-ω，0）在[-ω，ω]上有意义，则方程（4.1.1）至少存在一个2ω-周期解.

证 由上述条件知，s（t）≡αr（t）为方程组（4.1.3）的解.此时代数方程（4.1.6）的判别式为4n²（ω）+4αr²（ω）≥0，即方程（4.1.6）有根.

若r（ω）≠0，则s（ω）≠0，方程（4.1.6）的根为

又z（0）=1，则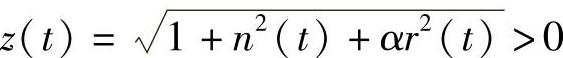，从而

由定理4.1.1知，此时方程（4.1.1）具有两个2ω-周期解.

若r（ω）=0，n（ω）≠0，此时方程（4.1.6）仅有一个根λ=0.由于解φ（t；-ω，0）在[-ω，ω]上有意义，由第2章基本引理2.1.1得，它为2ω-周期解.

若r（ω）=n（ω）=0，此时式（4.1.6）为恒等式，因此方程（4.1.1）在[-ω，ω]上有意义的解皆为2ω-周期解.

定理4.1.5 若a（t）为奇的2ω-周期连续函数，b（t），c（t）为连续的2ω-周期函数，满足关系式

b_o′（t）=2c_e（t）-a（t）b_e（t）b_o（t）.

则Riccati方程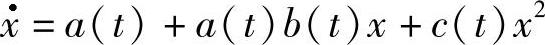具有反射函数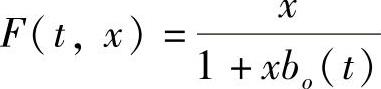，且其所有在[-ω，ω]上有定义的解皆为2ω-周期解.

证 在定理的条件下，方程（4.1.3）变为

其满足条件（4.1.4）的解为r（t）=n（t）=0，s（t）=b_o（t），z（t）≡1.因此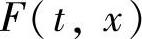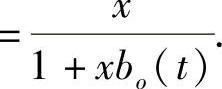又由于b_o（t）为奇的2ω-周期函数，则b_o（ω）=b_o（-ω），b_o（ω）=-b_o（-ω），从而b_o（-ω）=0，则F（-ω，x）≡x，由第2章的基本引理2.1.1得定理4.1.5的结论成立.

定理4.1.6 设Riccati方程

的系数函数为2ω-周期函数，且c（t）+c（-t）=0，b_o′（t）=cb_o（t）b_e（t）-2a_e（t）.则该Riccati方程（4.1.9）的反射函数为F（t，x）=x+b_o（t）.其在[-ω，ω]上有意义的解皆为2ω-周期解.

证 在该定理的条件下，方程组（4.1.3）变为

其满足初始条件（4.1.4）的解为n（t）=s（t）≡0，z（t）=1，r（t）=b_o（t）.因此方程（4.1.9）的反射函数为F（t，x）=x+b_o（t）.与定理4.1.5同理可证定理4.1.6的结论成立.

定理4.1.7 若方程（4.1.1）的系数函数都为2ω-周期函数，且满足

则当2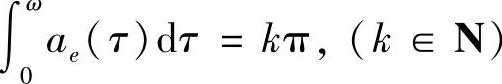时，方程（4.1.1）在[-ω，ω]上有意义的解皆为2ω-周期解.当2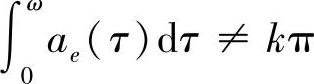时，方程（4.1.1）不存在2ω-周期解.

证 在上述定理的条件下，易验证

为方程（4.1.1）的反射函数.从而其Poincaré映射为T（x）=F（-ω，x）.由此即可推得定理4.1.7的结论成立.