这节我们将讨论二阶时变线性微分系统的反射矩阵的结构形式以及具有这些特征的反射矩阵的充要条件及其周期解的性态.
考虑线性微分系统
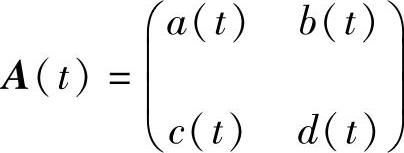 为连续矩阵函数.假设b(t)≠0,c(t)≠0.当它们中有一个恒等于零时,该线性系统可解出其通解,从而其反射矩阵就很容易求出.
为连续矩阵函数.假设b(t)≠0,c(t)≠0.当它们中有一个恒等于零时,该线性系统可解出其通解,从而其反射矩阵就很容易求出.
设
为系统(3.5.1)的反射函数.这里假设f2(t)≠0,当f2(t)≡0时,前面已经讨论过.在本节中记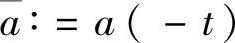 ,
, ,
,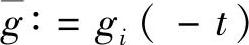 ,
,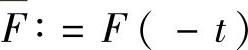 ,
,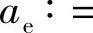
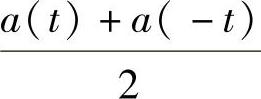 ,
,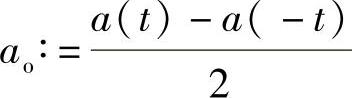 等等.
等等.
引理3.5.1 矩阵(3.5.2)为系统(3.5.1)的反射矩阵的充要条件为
F(t)=eα(t)G(t),其中
且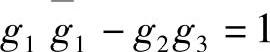 ,
, ,
,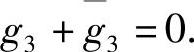 G(t)为线性微分系统
G(t)为线性微分系统
的反射矩阵.
这里
证F(t)为系统(3.5.1)的反射矩阵,当且仅当
由反射矩阵的性质得
由于式(3.5.5)等价于
由式(3.5.6)可得
f1f4-f2f3=e2α. (3.5.6)′
由式(3.5.7)可得
应用上面等式不难计算得
记g2=f2e-α,则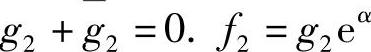 .将此代入式(3.5.7)′可得
.将此代入式(3.5.7)′可得
由于f2≠0,则g2≠0.记g1=f1e-α,则
再将所得结果代入式(3.5.7)′可得f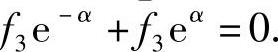 记g3=f3e-α,从而g3+g3=0,f3=g3eα.因此
记g3=f3e-α,从而g3+g3=0,f3=g3eα.因此
将此代入式(3.5.5)′可得
即G(t)是系统(3.5.4)的反射矩阵.
注3.5.1 由式(3.5.8)可推得,G(t)为系统(3.5.4)的反射函数,当且仅当
其中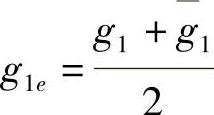 ,
,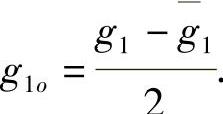
注3.5.2 由式(3.5.9)知,若ae∗=co=bo=0,则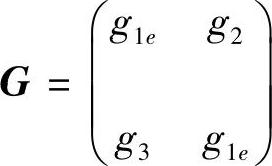 为系统(3.5.4)的反射矩阵,当且仅当
为系统(3.5.4)的反射矩阵,当且仅当
注3.5.3 由式(3.5.9)可知,若
则 是系统(3.5.4)的反射矩阵,其中
是系统(3.5.4)的反射矩阵,其中 ,
,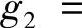

引理3.5.2 假设矩阵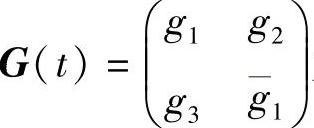 为系统(3.5.4)的反射矩阵,并且系统(3.5.4)是2ω-周期系统,则
为系统(3.5.4)的反射矩阵,并且系统(3.5.4)是2ω-周期系统,则
(1)若g1e(-ω)≠1,则系统(3.5.4)存在唯一的2ω-周期解,且当g1e(-ω)<1时该周期解稳定;当g1e(-ω)>1时不稳定;
(2)若g1e(-ω)=1时,则系统(3.5.4)存在无穷个2ω-周期解;
(3)若G(-ω)=E时,则系统(3.5.4)所有在[-ω,ω]上有意义的解皆为2ω-周期解;
证 由假设可知,2ω-周期系统(3.5.4)的Poincaré映射T(x,y)=G(-ω)x,则系统(3.5.4)的解x=φ(t;-ω,xo)为2ω-周期解,当且仅当,
(G(-ω)-E)xo=0.
又det(G(-ω)-E)=2(1-g1e(-ω)),由此可推得上述周期解的个数.至于这些周期解的稳定性的判定,由于det(G(-ω)-μE)=0的特征根就是周期系统(3.5.4)的特征乘子,由参考文献[28]即可推出引理的结论.
定理3.5.1 假设存在一个连续可微的奇函数β,满足下列条件:
(1) ,
,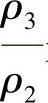 是连续可微的,且
是连续可微的,且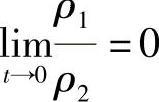 ;
;
(2)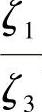 是连续可微的,且
是连续可微的,且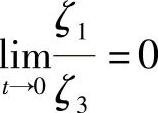 ;
;
(3)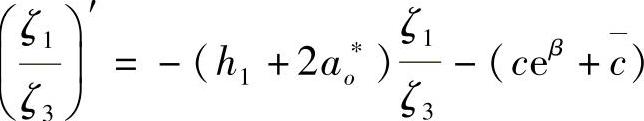 ;则
;则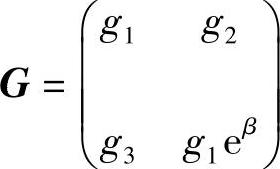 为系统(3.5.4)的反射矩阵.其中
为系统(3.5.4)的反射矩阵.其中
除此以外,若系统(3.5.4)为2ω-周期系统,则引理3.5.2的结论成立.
证 为了证明上述结论,只要验证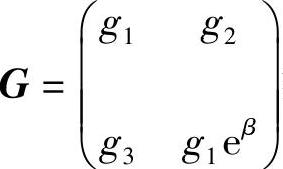 满足关系式(3.5.8).由ρ1,ρ2,ρ3的定义可得
满足关系式(3.5.8).由ρ1,ρ2,ρ3的定义可得
由此推出
应用
可得
由定理的条件(3)可推得 g3′=P3.
又由于
ζ3g3=ζ1g1, g2ρ2+ρ1g1+ρ3g3=0,
从而
即
综上得式(3.5.8)成立,从而定理得证.
取β=0时,由定理3.5.3推出.
推论3.5.1 假设:
(1)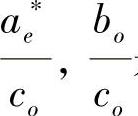 是连续可微的,
是连续可微的, ;
;
(2)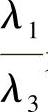 是连续可微的,且
是连续可微的,且 ;
;
则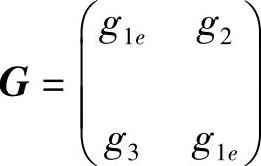 为系统(3.5.4)的反射矩阵.其中
为系统(3.5.4)的反射矩阵.其中
除此以外,若微分系统(3.5.4)是2ω-周期系统,则当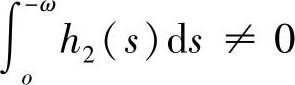 时,系统(3.5.4)存在唯一的2ω-周期解;并且该解当
时,系统(3.5.4)存在唯一的2ω-周期解;并且该解当 时稳定,当
时稳定,当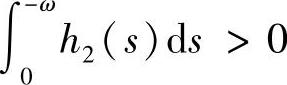 时不稳定;当
时不稳定;当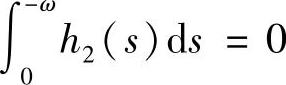 ,系统(3.5.4)存在无穷个2ω周期解;当G(-ω)=E时,系统(3.5.4)所有的解皆为2ω-周期解.同理我们可得:
,系统(3.5.4)存在无穷个2ω周期解;当G(-ω)=E时,系统(3.5.4)所有的解皆为2ω-周期解.同理我们可得:
定理3.5.2 假设存在一个连续可微的奇函数β,满足下列条件:
(1) ,
, 是连续可微的,且
是连续可微的,且 ;
;
(2) 是连续可微的,且
是连续可微的,且 ;(www.daowen.com)
;(www.daowen.com)
则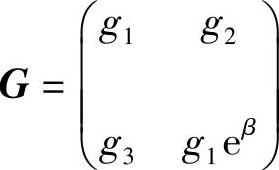 为系统(3.5.4)的反射矩阵.其中
为系统(3.5.4)的反射矩阵.其中
又当系统(3.5.4)为2ω-周期系统时,相应于引理3.5.2的结论成立.
在定理3.5.2中取β=0时,可得下面结论.
推论3.5.2 假设:
(1)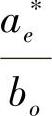 ,
, 是连续可微的,且
是连续可微的,且 ;
;
(2) 是连续可微的,且
是连续可微的,且 ;
;
则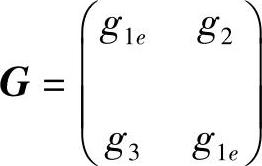 为系统(3.5.4)的反射矩阵.其中
为系统(3.5.4)的反射矩阵.其中
除此以外,若微分系统(3.5.4)是2ω-周期系统,则当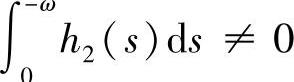 时,系统(3.5.4)存在唯一的2ω-周期解;并且该解当
时,系统(3.5.4)存在唯一的2ω-周期解;并且该解当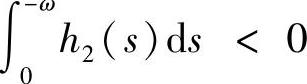 时稳定,当
时稳定,当 时不稳定;当
时不稳定;当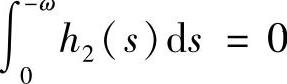 ,系统(3.5.4)存在无穷个2ω周期解;当G(-ω)=E时,系统(3.5.4)所有的解皆为2ω-周期解.
,系统(3.5.4)存在无穷个2ω周期解;当G(-ω)=E时,系统(3.5.4)所有的解皆为2ω-周期解.
例3.5.1 微分系统
具有反射矩阵
不难验证对于系统(3.5.10)推论3.5.1的条件都满足,这里
经过简单计算可得:
由于G(-π)=E,则由推论3.5.1得,微分系统(3.5.10)的所有解皆为2π-周期解.
例3.5.2 微分系统
具有反射矩阵
其中S∶=sint,T∶=cost.容易验证定理3.5.2的条件满足.其中
通过简单计算可得
由于G(-π)=E,由定理3.5.2推知,微分系统(3.5.11)定义在[-π,π]上的有意义的解皆为2π-周期解.
定理3.5.3 假设存在一个连续可微的偶函数k(t),满足以下条件:
(1)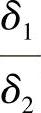 是连续可微的,且
是连续可微的,且 ;
;
(2) 是连续可微的,且
是连续可微的,且 ;
;
则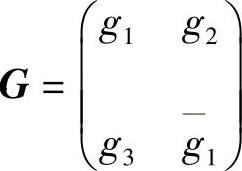 为系统(3.5.4)的反射矩阵.其中
为系统(3.5.4)的反射矩阵.其中
并且当系统(3.5.4)为2ω-周期系统时,相应于引理3.5.2的结论成立.
证 要想证明这个定理,只需验证矩阵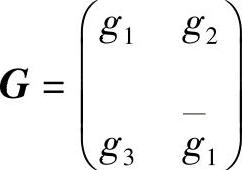 满足关系式(3.5.8).由定理条件可得
满足关系式(3.5.8).由定理条件可得
即 g1′=h5g1=P1.
又由条件(3)得
由于
则有
从而有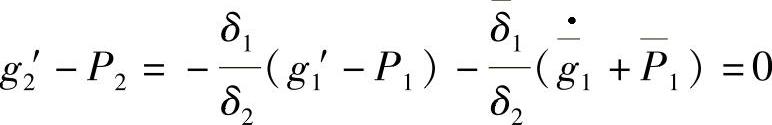 ,即g2′=P2.
,即g2′=P2.
再由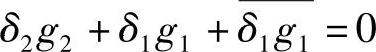 ,得P3=k′g2+kP2.从而有
,得P3=k′g2+kP2.从而有
g3′-P3=k(g2′-P2)=0.
综上可得,矩阵G(t)满足式(3.5.8),即G(t)为系统(3.5.4)的反射矩阵,再由引理3.5.2定理得证.
在上述定理中,取可得下面推论.
推论3.5.3 假设
(1)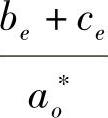 ,
,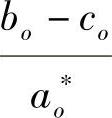 连续可微,且
连续可微,且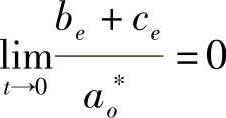 ;
;
(2) 连续可微,且
连续可微,且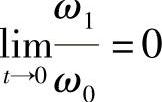 ;
;
则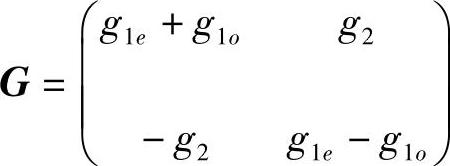 为系统(3.5.4)的反射矩阵.其中
为系统(3.5.4)的反射矩阵.其中
除此以外,若微分系统(3.5.4)是2ω-周期系统,则当 时,系统(3.5.4)存在唯一的2ω-周期解;并且该解当
时,系统(3.5.4)存在唯一的2ω-周期解;并且该解当 时稳定,当
时稳定,当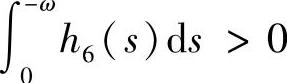 时不稳定;当
时不稳定;当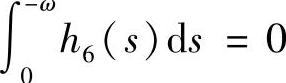 ,系统(3.5.4)存在无穷个2ω周期解;当G(-ω)=E时,系统(3.5.4)所有的解皆为2ω-周期解.
,系统(3.5.4)存在无穷个2ω周期解;当G(-ω)=E时,系统(3.5.4)所有的解皆为2ω-周期解.
证 为了证明这个推论的结论,只需验证G(t)满足式(3.5.9).由于
 ,则g′1e=h6g1e.又由g1o,g2,b6的表达式可得
,则g′1e=h6g1e.又由g1o,g2,b6的表达式可得
Q1=-2ae∗g1o-g2ce-beg3=h6g1e,
则 g′1e=Q1.又由于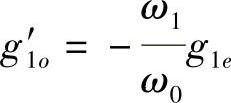 ,则
,则
应用条件(3)可推得
又由ω2g1e+wog1o=0可得
因此
由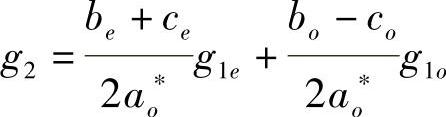 得,Q2=-Q3,以及g3′-Q3=-(g2′-Q2)=0.综上得G(t)满足(3.5.9),从而推论的结论成立.同理可得:
得,Q2=-Q3,以及g3′-Q3=-(g2′-Q2)=0.综上得G(t)满足(3.5.9),从而推论的结论成立.同理可得:
定理3.5.4 假设存在一个连续可微的偶函数k(t),满足以下条件:
(1) ,是连续可微的,且
,是连续可微的,且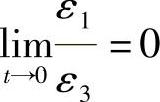 ;
;
(2) 是连续可微的,且
是连续可微的,且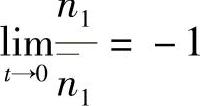 ;
;
则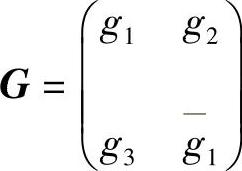 为系统(3.5.4)的反射矩阵.其中
为系统(3.5.4)的反射矩阵.其中
并且当系统(3.5.4)为2ω-周期系统时,相应于引理3.5.2的结论成立.
在定理3.5.4中取k=1可得下面结论:
推论3.5.4 假设
(1) ,
,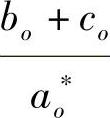 连续可微,且
连续可微,且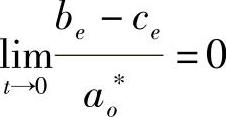 ;
;
(2)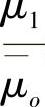 连续可微,且
连续可微,且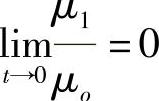 ;
;
则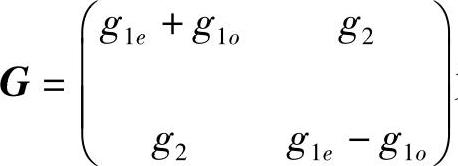 为系统(3.5.4)的反射矩阵.其中
为系统(3.5.4)的反射矩阵.其中
除此以外,若微分系统(3.5.4)是2ω-周期系统,则当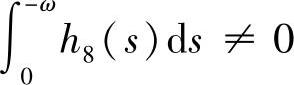 时,系统(3.5.4)存在唯一的2ω-周期解;并且该解当
时,系统(3.5.4)存在唯一的2ω-周期解;并且该解当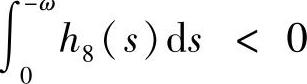 时稳定,当
时稳定,当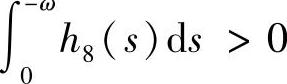 时不稳定;当
时不稳定;当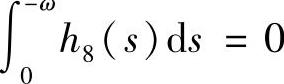 ,系统(3.5.4)存在无穷个2ω-周期解;当G(-ω)=E时,系统(3.5.4)所有的解皆为2ω-周期解.
,系统(3.5.4)存在无穷个2ω-周期解;当G(-ω)=E时,系统(3.5.4)所有的解皆为2ω-周期解.
注3.5.4 若上述定理或推论之一的条件成立,则F(t,x)=eα(t)G(t)x为系统(3.5.1)的反射矩阵.并且当系统(3.5.1)为2ω-周期系统时,当
 时,系统(3.5.1)存在唯一的2ω-周期解,当g1e(ω)e-α(ω)<1时稳定,当g1e(ω)e-α(ω)>1时不稳定.如果
时,系统(3.5.1)存在唯一的2ω-周期解,当g1e(ω)e-α(ω)<1时稳定,当g1e(ω)e-α(ω)>1时不稳定.如果 时,此时系统(3.5.1)有无穷个2ω-周期解.当F(-ω)=e-α(ω)G(-ω)=E时,系统(3.5.1)在[-ω,ω]上有意义的解皆为2ω-周期解.
时,此时系统(3.5.1)有无穷个2ω-周期解.当F(-ω)=e-α(ω)G(-ω)=E时,系统(3.5.1)在[-ω,ω]上有意义的解皆为2ω-周期解.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






